回溯法
基本思想:
构建问题的解空间树,在其解空间树中,从根节点出发,进行深度优先搜索。在搜索过程中,对解空间
树的每个结点进行判断,判断该结点是否包含问题的解,若肯定不包含,则跳过对以该结点为根的子树的
搜索,逐层向其祖先结点回溯。否则,则进入该子树,继续按深度优先策略搜索。
步骤:
1、针对所给问题,定义其解空间
2、确定易于搜索的解空间结构
3、深度优先搜索其解空间,并在搜索过程中用剪枝函数避免无效搜索
剪枝:
回溯法搜索空间树时,常用限界函数和约束函数避免无效搜索,其中约束函数将不满足约束的子树剪去,
限界函数将得不到最优解的子树。一般可以利用这两种剪枝方式提升算法的效率,避免大量的不必要搜索。
常见解空间:
常见的解空间有子集树和排列树两种,当问题是从n个元素的集合S中找到满足某种性质的s的子集时,相应的
解空间为子集树,通常存在2n个叶结点。0-1背包的问题相应解空间即为子集树。当问题是确定n个元素的满足
某种性质的序列时,相应的解空间树为排列树通常有n!个叶结点。旅行售货问题的解空间即为排列树。
个人理解:
学习了回溯法后,个人感觉回溯法就是通过对解空间的遍历,在解空间不断更新答案,最后找到最优的结果。
回溯法最主要的是三点,一是构造问题的解空间,不同问题的解空间不同,同一个问题也可以构造不同的解空间,
最适合的解空间是便通过于搜索找到答案的一种。二是搜索策略,回溯法用的是深度优先搜索策略,在回溯是需要
注意对一些变量的处理操作。三是剪枝,剪枝是回溯法的精髓所在,通过剪枝去掉大量不必要的搜索可以大幅的提
高算法的效率,因此回溯法构造合理的剪枝方式可以决定算法的优劣,十分重要。
例题说明:
7-1 子集和问题
问题描述:存在一个正整数集合S={x1,x2,…,xn},c是一个整数,判读S是否存在一个子集s1,子集的和等于c
//输入 5 10 //5个数字的集合S c为10 2 2 6 5 4 //输出 2 2 6
解空间:
子集和问题的解空间为子集树结构。其中子集树的每一层表示是否选择该数值。
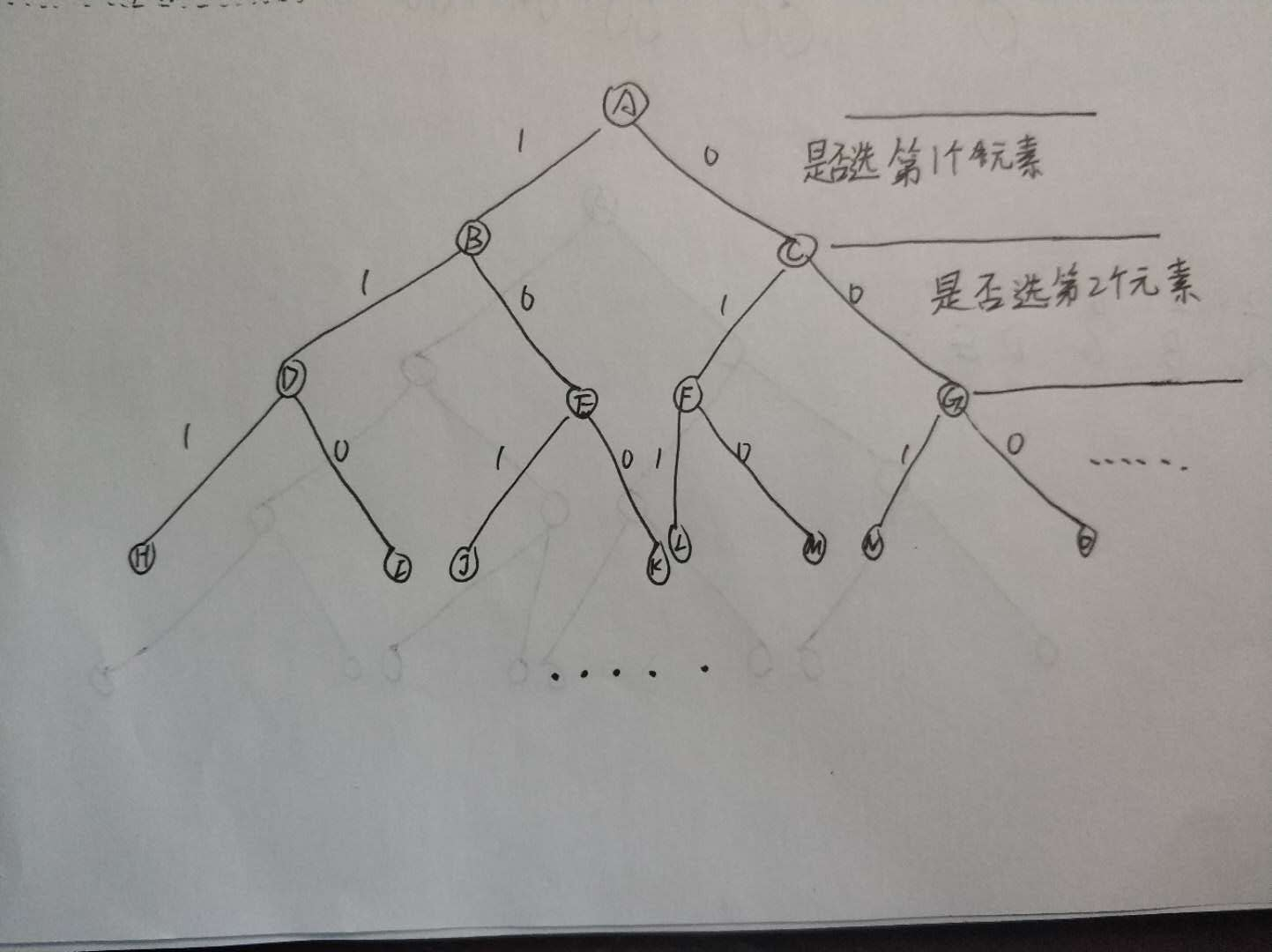
约束函数:
当递归的层数大于等于n时,表示当前层次已经大于元素的个数,接下来的为无用搜索,直接剪去该
结点的搜索即可当搜索到当前结点后所得的值大于题目中的c,则表示接下来的搜索不可能找到等于c的
答案,直接剪去以该节为根的子树的搜索即可。
if(i>=n||c<ans) //ans为遍历到该节点时,所选择的元素的和 return; if(ans+a[i]<=c) //第i个元素是否加入子集 if(ans<=c)
结对编程以及学习心得:
在本章学习中,了解了回溯法的基本用法,对于大部分的题目中,都可以利用回溯法来解出他的答案,主要
难点是构造解空间和搜索时的剪枝的方法,剪枝的方法会影响到算法的最终效率,需要多加考虑。在本次结对编程
中,还是存在一些小问题,对同一题的不同想法等,在不断的交流中加深了对回溯法的理解,对学习理解有一定的帮助促进效果。