第七章小结
先简单介绍了一下查找的概念
查找主要分为线性表和树表的查找。
线性表又分为顺序、折半和分块查找。
其中我们重点分析了这三种查找的时间和空间复杂度,也提了一下他们的适用范围和优缺点。
顺序查找:适用于线性表的顺序存储结构,又适用于链式存储结构;时间复杂度O(n),空间复杂度O(1)
优点:算法简单,对表结构没有要求,且对记录是否按关键字有序均可应用
缺点:平均查找长度较大,查找效率较低,n很大的时候不适合用
折半查找:线性表必须采用顺序存储结构,而且表中的元素按关键字有序排列;时间复杂度O(log2 n)
优点:比较次数少,查找效率高;
缺点:对表的要求高,一定要是顺序存储,且关键字必须有序;费时:
分块查找:
优点:.在表中插入和删除元素时,只要找到该元素对应的块,就可以在该块内进行插入和删除;适用于动态变化的线性表
缺点:要增加一个索引表的存储空间并对索引表进行排序运算
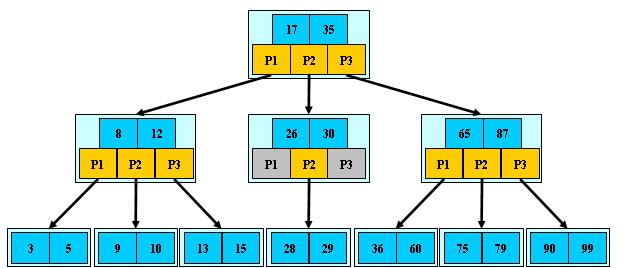
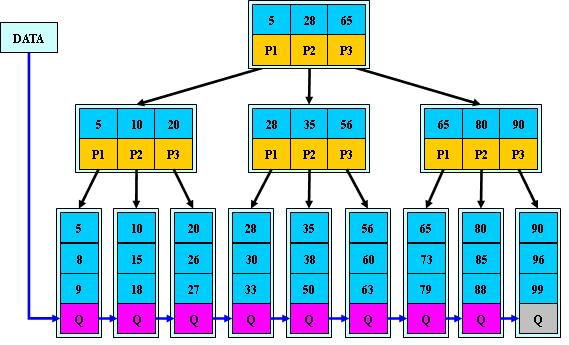
树表主要分为二叉排序树、平衡二叉树、B-树和B+树
其中B树
和B+树
B+的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好
是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储
(关键字)数据的数据层;
4.更适合文件索引系统;
所以说,B+树是在B-树基础上的升级。
最后是散列表的查找
哈希表查找
构造方法:1)数字分析法;2)平方取中法;3)折叠法;4)除留余数法
处理冲突的方法:1)开放地址法
Hi=(H(key)+di)%m(H(key)为散列函数,m为散列表表长,di为增量序列)
三种探测方法:
①线性探测法:di=1,2,3......
②二次探测法:di=1²,-1²,2²,-2².......+k²,-k²(k<=m/2)
③伪随机探测法:di=伪随机数序列
2)链地址法:把具有相同散列地址的记录放在同一个单链表中,称为“同义词链表”
最后在作业中也有一道使用哈希查找的题
在此贴出
#include<iostream> #include<cmath> using namespace std; int largestPrime(int MSize); int main() { int MSize,N;//MSize是哈希表的表长,N是将要插入的数 cin >> MSize >> N; int prime = largestPrime(MSize); bool *Hashtable ;//将表中所有地址置为不冲突 Hashtable = new bool[MSize+1]; for(int i =0;i<=MSize;i++) Hashtable[i] = false; int num,H;//准备插入的正整数 num,准备插入的num的地址H for(int i = 0;i < N;i++) { cin >> num; int j = 0; int flag = 0; H = num % prime; int temp = H; //用来存储最初的下标 while(1) { if(j >= prime) break; if(Hashtable[H] == false) { Hashtable[H] = true; if (i > 0) cout << " "; cout << H; flag = 1; break; } H = (temp + j*j) % prime; j++; //如果不是空位,就j++ } if(flag == 1) continue; if(i > 0) cout << " "; cout<< "-"; } cout << endl; return 0; } int largestPrime(int MSize) {//找到最大的质数 if(MSize<=2) return 2; bool Find = true; int i; while(Find) { int Prime = sqrt(MSize);//以表长的算术平方根为界限 for(i = 2;i<=Prime&&MSize%i !=0;i++){}; if(i > Prime) Find = false; else MSize++; } return MSize;//返回最大的质数 }
最后是对上次的目标的小结,完成的还算满意,课堂上听的也基本能听懂,代码也能自己去构思, 然后六月了,应该要开始准备复习了。