zoukankan      html  css  js  c++  java

  • 13、【堆】斐波那契堆

    一、斐波那契堆的介绍

    斐波那契堆(Fibonacci heap)是堆中一种，它和二项堆一样，也是一种可合并堆；可用于实现合并优先队列。斐波那契堆比二项堆具有更好的平摊分析性能，它的合并操作的时间复杂度是O(1)。
    与二项堆一样，它也是由一组堆最小有序树组成，并且是一种可合并堆。
    与二项堆不同的是，斐波那契堆中的树不一定是二项树；而且二项堆中的树是有序排列的，但是斐波那契堆中的树都是有根而无序的。

    二、斐波那契堆的基本操作

    1. 基本定义

     1 template <class T>
 2 class FibNode {
 3     public:
 4         T key;                // 关键字(键值)
 5         int degree;            // 度数
 6         FibNode<T> *left;    // 左兄弟
 7         FibNode<T> *right;    // 右兄弟
 8         FibNode<T> *child;    // 第一个孩子节点
 9         FibNode<T> *parent;    // 父节点
10         bool marked;        // 是否被删除第一个孩子
11 
12         FibNode(T value):key(value), degree(0), marked(false), 
13             left(NULL),right(NULL),child(NULL),parent(NULL) {
14             key    = value;
15             degree = 0;
16             marked = false;
17             left   = this;
18             right  = this;
19             parent = NULL;
20             child  = NULL;
21         }
22 };

    FibNode是斐波那契堆的节点类，它包含的信息较多。key是用于比较节点大小的，degree是记录节点的度，left和right分别是指向节点的左右兄弟，child是节点的第一个孩子，parent是节点的父节点，marked是记录该节点是否被删除第1个孩子(marked在删除节点时有用)。

     1 template <class T>
 2 class FibHeap {
 3     private:
 4         int keyNum;         // 堆中节点的总数
 5         int maxDegree;      // 最大度
 6         FibNode<T> *min;    // 最小节点(某个最小堆的根节点)
 7         FibNode<T> **cons;    // 最大度的内存区域
 8 
 9     public:
10         FibHeap();
11         ~FibHeap();
12 
13         // 新建key对应的节点，并将其插入到斐波那契堆中
14         void insert(T key);
15         // 移除斐波那契堆中的最小节点
16         void removeMin();
17         // 将other合并到当前堆中
18         void combine(FibHeap<T> *other);
19         // 获取斐波那契堆中最小键值，并保存到pkey中；成功返回true，否则返回false。
20         bool minimum(T *pkey);
21         // 将斐波那契堆中键值oldkey更新为newkey
22         void update(T oldkey, T newkey);
23         // 删除键值为key的节点
24         void remove(T key);
25         // 斐波那契堆中是否包含键值key
26         bool contains(T key);
27         // 打印斐波那契堆
28         void print();
29         // 销毁
30         void destroy();
31 
32     private:
33         // 将node从双链表移除
34         void removeNode(FibNode<T> *node);
35         // 将node堆结点加入root结点之前(循环链表中)
36         void addNode(FibNode<T> *node, FibNode<T> *root);
37         // 将双向链表b链接到双向链表a的后面
38         void catList(FibNode<T> *a, FibNode<T> *b);
39         // 将节点node插入到斐波那契堆中
40         void insert(FibNode<T> *node);
41         // 将"堆的最小结点"从根链表中移除，
42         FibNode<T>* extractMin();
43         // 将node链接到root根结点
44         void link(FibNode<T>* node, FibNode<T>* root);
45         // 创建consolidate所需空间
46         void makeCons();
47         // 合并斐波那契堆的根链表中左右相同度数的树
48         void consolidate();
49         // 修改度数
50         void renewDegree(FibNode<T> *parent, int degree);
51         // 将node从父节点parent的子链接中剥离出来，并使node成为"堆的根链表"中的一员。
52         void cut(FibNode<T> *node, FibNode<T> *parent);
53         // 对节点node进行"级联剪切"
54         void cascadingCut(FibNode<T> *node) ;
55         // 将斐波那契堆中节点node的值减少为key
56         void decrease(FibNode<T> *node, T key);
57         // 将斐波那契堆中节点node的值增加为key
58         void increase(FibNode<T> *node, T key);
59         // 更新斐波那契堆的节点node的键值为key
60         void update(FibNode<T> *node, T key);
61         // 在最小堆root中查找键值为key的节点
62         FibNode<T>* search(FibNode<T> *root, T key);
63         // 在斐波那契堆中查找键值为key的节点
64         FibNode<T>* search(T key);
65         // 删除结点node
66         void remove(FibNode<T> *node);
67         // 销毁斐波那契堆
68         void destroyNode(FibNode<T> *node);
69         // 打印"斐波那契堆"
70         void print(FibNode<T> *node, FibNode<T> *prev, int direction);
71 };

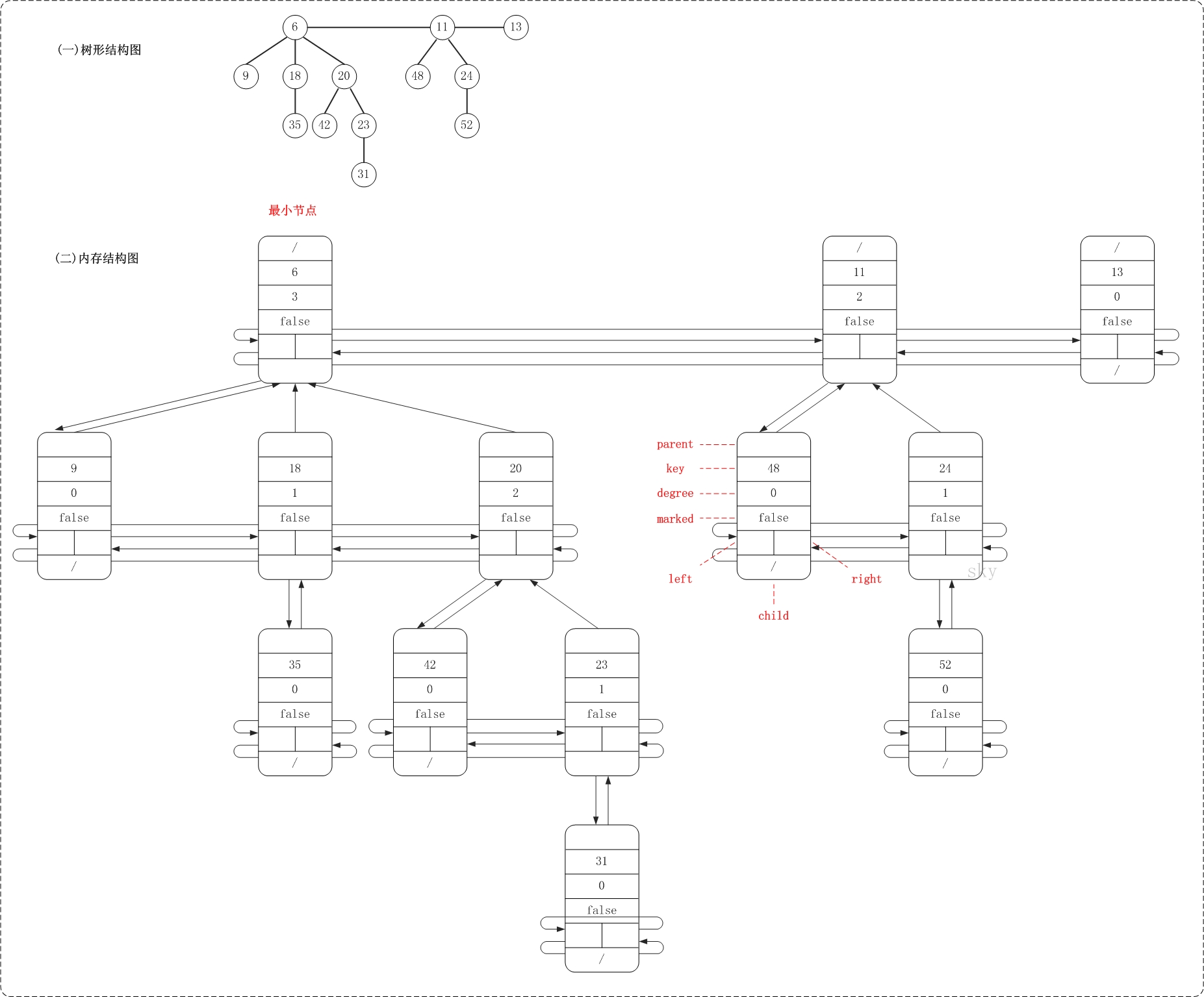
    FibHeap是斐波那契堆对应的类。min是保存当前堆的最小节点，keyNum用于记录堆中节点的总数，maxDegree用于记录堆中最大度，而cons在删除节点时来暂时保存堆数据的临时空间。下面是斐波那契堆的属性结构图和内存结构图的对比示例。

    从中可以看出，斐波那契堆是由一组最小堆组成，这些最小堆的根节点组成了双向链表(后文称为"根链表")；斐波那契堆中的最小节点就是"根链表中的最小节点"！

    2. 插入操作

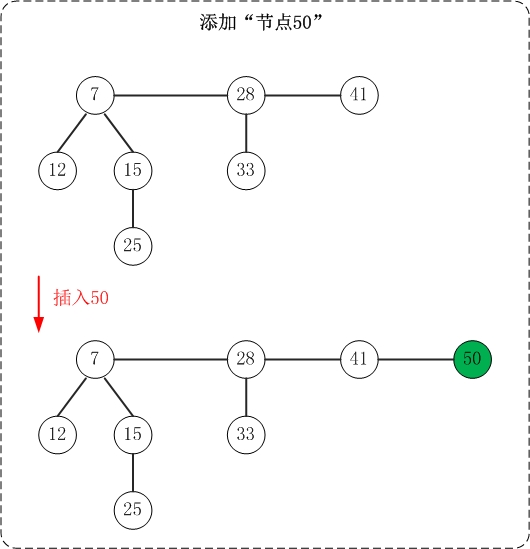
    插入操作非常简单：插入一个节点到堆中，直接将该节点插入到"根链表的min节点"之前即可；若被插入节点比"min节点"小，则更新"min节点"为被插入节点。

    上面是插入操作的示意图。

    斐波那契堆的根链表是"双向链表"，这里将min节点看作双向联表的表头(后文也是如此)。在插入节点时，每次都是"将节点插入到min节点之前(即插入到双链表末尾)"。此外，对于根链表中最小堆都只有一个节点的情况，插入操作就很演化成双向链表的插入操作。

    此外，插入操作示意图与测试程序中的"插入操作"相对应，感兴趣的可以亲自验证。

    插入操作代码

     1 /*
 2  * 将node堆结点加入root结点之前(循环链表中)
 3  *   a …… root
 4  *   a …… node …… root
 5 */
 6 template <class T>
 7 void FibHeap<T>::addNode(FibNode<T> *node, FibNode<T> *root)
 8 {
 9     node->left        = root->left;
10     root->left->right = node;
11     node->right       = root;
12     root->left        = node;
13 }
14  
15 /*
16  * 将节点node插入到斐波那契堆中
17  */
18 template <class T>
19 void FibHeap<T>::insert(FibNode<T> *node)
20 {
21     if (keyNum == 0)
22         min = node;
23     else
24        {
25         addNode(node, min);
26         if (node->key < min->key)
27             min = node;
28     }
29     keyNum++;
30 }

    3. 合并操作

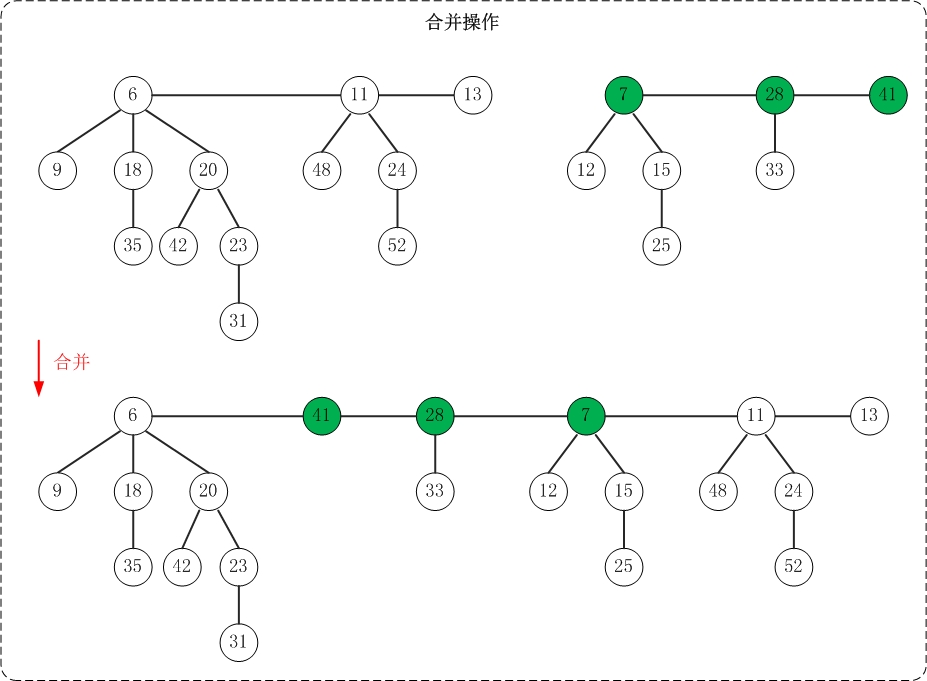
    合并操作和插入操作的原理非常类似：将一个堆的根链表插入到另一个堆的根链表上即可。简单来说，就是将两个双链表拼接成一个双向链表。

    上面是合并操作的示意图。该操作示意图与测试程序中的"合并操作"相对应！

    合并操作代码

     1 /*
 2  * 将双向链表b链接到双向链表a的后面
 3  *
 4  * 注意： 此处a和b都是双向链表
 5  */
 6 template <class T>
 7 void FibHeap<T>::catList(FibNode<T> *a, FibNode<T> *b)
 8 {
 9     FibNode<T> *tmp;
10 
11     tmp            = a->right;
12     a->right       = b->right;
13     b->right->left = a;
14     b->right       = tmp;
15     tmp->left      = b;
16 }
17 
18   
19 /*
20  * 将other合并到当前堆中
21  */
22 template <class T>
23 void FibHeap<T>::combine(FibHeap<T> *other)
24 {
25     if (other==NULL)
26         return ;
27 
28     if(other->maxDegree > this->maxDegree)
29         swap(*this, *other);
30 
31     if((this->min) == NULL)                // this无"最小节点"
32     {
33         this->min = other->min;
34         this->keyNum = other->keyNum;
35         free(other->cons);
36         delete other;
37     }
38     else if((other->min) == NULL)           // this有"最小节点" && other无"最小节点"
39     {
40         free(other->cons);
41         delete other;
42     }                                       // this有"最小节点" && other有"最小节点"
43     else
44     {
45         // 将"other中根链表"添加到"this"中
46         catList(this->min, other->min);
47 
48         if (this->min->key > other->min->key)
49             this->min = other->min;
50         this->keyNum += other->keyNum;
51         free(other->cons);
52         delete other;
53     }
54 }

    4. 取出最小节点

    抽取最小结点的操作是斐波那契堆中较复杂的操作。
    (1）将要抽取最小结点的子树都直接串联在根表中；
    (2）合并所有degree相等的树，直到没有相等的degree的树。

    上面是取出最小节点的示意图。图中应该写的非常明白了，若有疑问，看代码。

    此外，该操作示意图与测试程序中的"删除最小节点"相对应！有兴趣的可以亲自验证。

    取出最小节点代码

      1 /*
  2  * 将"堆的最小结点"从根链表中移除，
  3  * 这意味着"将最小节点所属的树"从堆中移除!
  4  */
  5 template <class T>
  6 FibNode<T>* FibHeap<T>::extractMin()
  7 {
  8     FibNode<T> *p = min;
  9 
 10     if (p == p->right)
 11         min = NULL;
 12     else
 13     {
 14         removeNode(p);
 15         min = p->right;
 16     }
 17     p->left = p->right = p;
 18 
 19     return p;
 20 }
 21  
 22 /*
 23  * 将node链接到root根结点
 24  */
 25 template <class T>
 26 void FibHeap<T>::link(FibNode<T>* node, FibNode<T>* root)
 27 {
 28     // 将node从双链表中移除
 29     removeNode(node);
 30     // 将node设为root的孩子
 31     if (root->child == NULL)
 32         root->child = node;
 33     else
 34         addNode(node, root->child);
 35 
 36     node->parent = root;
 37     root->degree++;
 38     node->marked = false;
 39 }
 40  
 41 /* 
 42  * 创建consolidate所需空间
 43  */
 44 template <class T>
 45 void FibHeap<T>::makeCons()
 46 {
 47     int old = maxDegree;
 48 
 49     // 计算log2(keyNum)，"+1"意味着向上取整！
 50     // ex. log2(13) = 3，向上取整为3+1=4。
 51     maxDegree = (log(keyNum)/log(2.0)) + 1;
 52     if (old >= maxDegree)
 53         return ;
 54 
 55     // 因为度为maxDegree可能被合并，所以要maxDegree+1
 56     cons = (FibNode<T> **)realloc(cons, 
 57             sizeof(FibHeap<T> *) * (maxDegree + 1));
 58 }
 59 
 60 /* 
 61  * 合并斐波那契堆的根链表中左右相同度数的树
 62  */
 63 template <class T>
 64 void FibHeap<T>::consolidate()
 65 {
 66     int i, d, D;
 67     FibNode<T> *x, *y, *tmp;
 68 
 69     makeCons();//开辟哈希所用空间
 70     D = maxDegree + 1;
 71 
 72     for (i = 0; i < D; i++)
 73         cons[i] = NULL;
 74  
 75     // 合并相同度的根节点，使每个度数的树唯一
 76     while (min != NULL)
 77     {
 78         x = extractMin();                // 取出堆中的最小树(最小节点所在的树)
 79         d = x->degree;                    // 获取最小树的度数
 80         // cons[d] != NULL，意味着有两棵树(x和y)的"度数"相同。
 81         while (cons[d] != NULL)
 82         {
 83             y = cons[d];                // y是"与x的度数相同的树" 
 84             if (x->key > y->key)        // 保证x的键值比y小
 85                 swap(x, y);
 86 
 87             link(y, x);    // 将y链接到x中
 88             cons[d] = NULL;
 89             d++;
 90         }
 91         cons[d] = x;
 92     }
 93     min = NULL;
 94  
 95     // 将cons中的结点重新加到根表中
 96     for (i=0; i<D; i++)
 97     {
 98         if (cons[i] != NULL)
 99         {
100             if (min == NULL)
101                 min = cons[i];
102             else
103             {
104                 addNode(cons[i], min);
105                 if ((cons[i])->key < min->key)
106                     min = cons[i];
107             }
108         }
109     }
110 }
111  
112 /*
113  * 移除最小节点
114  */
115 template <class T>
116 void FibHeap<T>::removeMin()
117 {
118     if (min==NULL)
119         return ;
120 
121     FibNode<T> *child = NULL;
122     FibNode<T> *m = min;
123     // 将min每一个儿子(儿子和儿子的兄弟)都添加到"斐波那契堆的根链表"中
124     while (m->child != NULL)
125     {
126         child = m->child;
127         removeNode(child);
128         if (child->right == child)
129             m->child = NULL;
130         else
131             m->child = child->right;
132 
133         addNode(child, min);
134         child->parent = NULL;
135     }
136 
137     // 将m从根链表中移除
138     removeNode(m);
139     // 若m是堆中唯一节点，则设置堆的最小节点为NULL；
140     // 否则，设置堆的最小节点为一个非空节点(m->right)，然后再进行调节。
141     if (m->right == m)
142         min = NULL;
143     else
144     {
145         min = m->right;
146         consolidate();
147     }
148     keyNum--;
149 
150     delete m;
151 }

    5. 减小节点值

    减少斐波那契堆中的节点的键值，这个操作的难点是：如果减少节点后破坏了"最小堆"性质，如何去维护呢？下面对一般性情况进行分析。
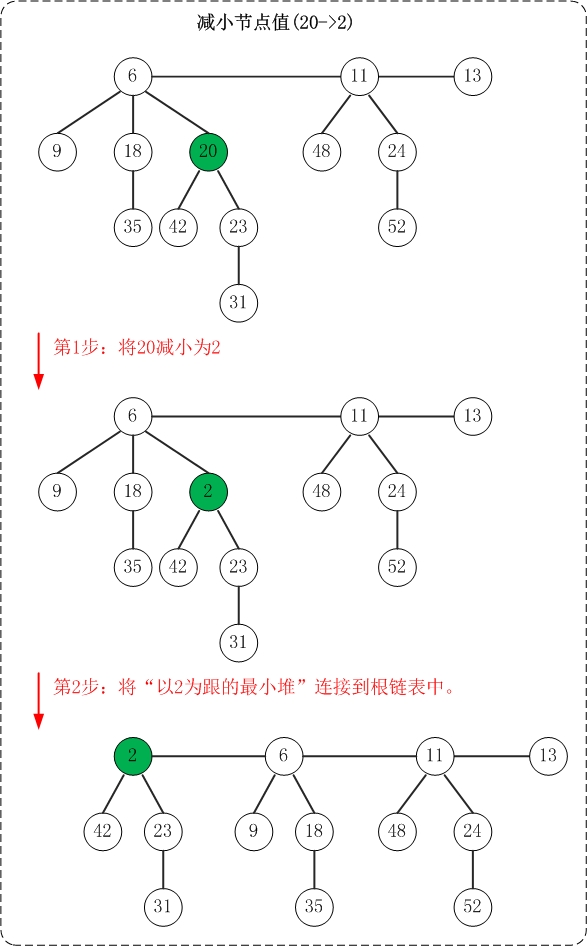
    　　(1) 首先，将"被减小节点"从"它所在的最小堆"剥离出来；然后将"该节点"关联到"根链表"中。 倘若被减小的节点不是单独一个节点，而是包含子树的树根。则是将以"被减小节点"为根的子树从"最小堆"中剥离出来，然后将该树关联到根链表中。
    　　(2) 接着，对"被减少节点"的原父节点进行"级联剪切"。所谓"级联剪切"，就是在被减小节点破坏了最小堆性质，并被切下来之后；再从"它的父节点"进行递归级联剪切操作。
          而级联操作的具体动作则是：若父节点(被减小节点的父节点)的marked标记为false，则将其设为true，然后退出。
    　　否则，将父节点从最小堆中切下来(方式和"切被减小节点的方式"一样)；然后递归对祖父节点进行"级联剪切"。
          marked标记的作用就是用来标记"该节点的子节点是否有被删除过"，它的作用是来实现级联剪切。而级联剪切的真正目的是为了防止"最小堆"由二叉树演化成链表。
    　　(3) 最后，别忘了对根链表的最小节点进行更新。

    上面是减小节点值的示意图。该操作示意图与测试程序中的"减小节点"相对应！

    减小节点值的代码

     1 /* 
 2  * 修改度数
 3  */
 4 template <class T>
 5 void FibHeap<T>::renewDegree(FibNode<T> *parent, int degree)
 6 {
 7     parent->degree -= degree;
 8     if (parent-> parent != NULL)
 9         renewDegree(parent->parent, degree);
10 }
11  
12 /* 
13  * 将node从父节点parent的子链接中剥离出来，
14  * 并使node成为"堆的根链表"中的一员。
15  */
16 template <class T>
17 void FibHeap<T>::cut(FibNode<T> *node, FibNode<T> *parent)
18 {
19     removeNode(node);
20     renewDegree(parent, node->degree);
21     // node没有兄弟
22     if (node == node->right) 
23         parent->child = NULL;
24     else 
25         parent->child = node->right;
26 
27     node->parent = NULL;
28     node->left = node->right = node;
29     node->marked = false;
30     // 将"node所在树"添加到"根链表"中
31     addNode(node, min);
32 }
33 
34 /* 
35  * 对节点node进行"级联剪切"
36  *
37  * 级联剪切：如果减小后的结点破坏了最小堆性质，
38  *     则把它切下来(即从所在双向链表中删除，并将
39  *     其插入到由最小树根节点形成的双向链表中)，
40  *     然后再从"被切节点的父节点"到所在树根节点递归执行级联剪枝
41  */
42 template <class T>
43 void FibHeap<T>::cascadingCut(FibNode<T> *node) 
44 {
45     FibNode<T> *parent = node->parent;
46     if (parent != NULL)
47     {
48         if (node->marked == false) 
49             node->marked = true;
50         else
51         {
52             cut(node, parent);
53             cascadingCut(parent);
54         }
55     }
56 }
57 
58 /* 
59  * 将斐波那契堆中节点node的值减少为key
60  */
61 template <class T>
62 void FibHeap<T>::decrease(FibNode<T> *node, T key)
63 {
64     FibNode<T> *parent;
65 
66     if (min==NULL ||node==NULL) 
67         return ;
68 
69     if ( key>=node->key)
70     {
71         cout << "decrease failed: the new key(" << key <<") "
72              << "is no smaller than current key(" << node->key <<")" << endl;
73         return ;
74     }
75 
76     node->key = key;
77     parent = node->parent;
78     if (parent!=NULL && node->key < parent->key)
79     {
80         // 将node从父节点parent中剥离出来，并将node添加到根链表中
81         cut(node, parent);
82         cascadingCut(parent);
83     }
84 
85     // 更新最小节点
86     if (node->key < min->key)
87         min = node;
88 }

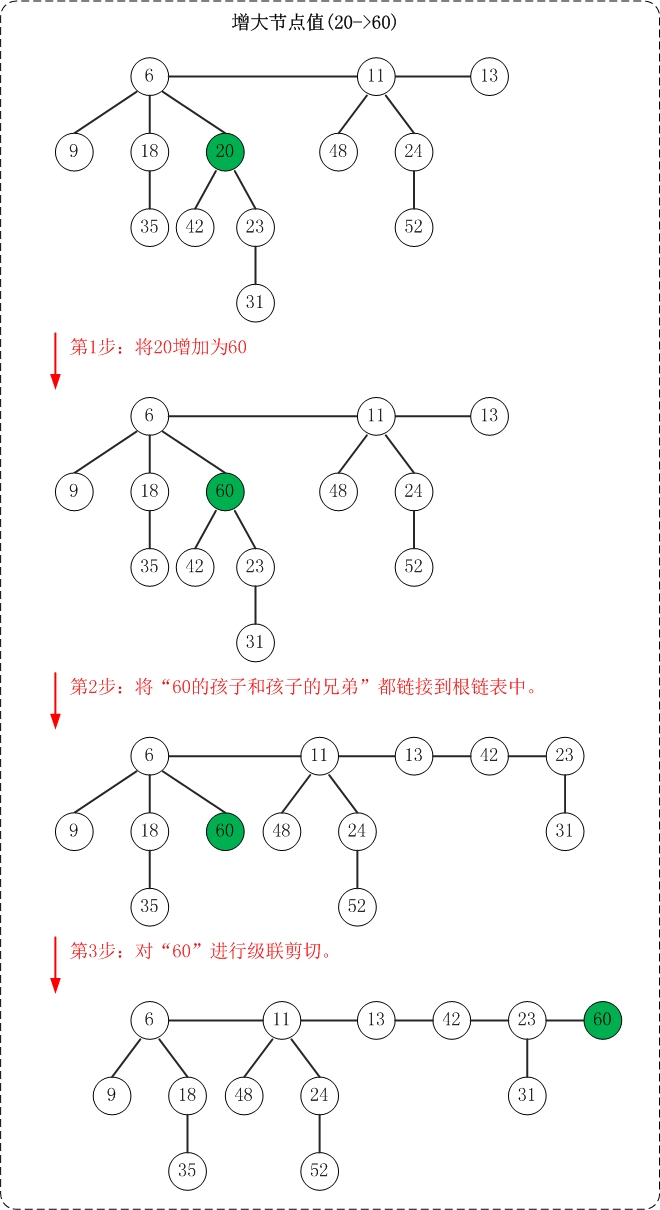
    6. 增加节点值

    增加节点值和减少节点值类似，这个操作的难点也是如何维护"最小堆"性质。思路如下：
    (1) 将"被增加节点"的"左孩子和左孩子的所有兄弟"都链接到根链表中。
    (2) 接下来，把"被增加节点"添加到根链表；但是别忘了对其进行级联剪切。

    上面是增加节点值的示意图。该操作示意图与测试程序中的"增大节点"相对应！

    增加节点值的代码

     1 /* 
 2  * 将斐波那契堆中节点node的值增加为key
 3  */
 4 template <class T>
 5 void FibHeap<T>::increase(FibNode<T> *node, T key)
 6 {
 7     FibNode<T> *child, *parent, *right;
 8 
 9     if (min==NULL ||node==NULL) 
10         return ;
11 
12     if (key <= node->key)
13     {
14         cout << "increase failed: the new key(" << key <<") " 
15              << "is no greater than current key(" << node->key <<")" << endl;
16         return ;
17     }
18 
19     // 将node每一个儿子(不包括孙子,重孙,...)都添加到"斐波那契堆的根链表"中
20     while (node->child != NULL)
21     {
22         child = node->child;
23         removeNode(child);               // 将child从node的子链表中删除
24         if (child->right == child)
25             node->child = NULL;
26         else
27             node->child = child->right;
28 
29         addNode(child, min);       // 将child添加到根链表中
30         child->parent = NULL;
31     }
32     node->degree = 0;
33     node->key = key;
34 
35     // 如果node不在根链表中，
36     //     则将node从父节点parent的子链接中剥离出来，
37     //     并使node成为"堆的根链表"中的一员，
38     //     然后进行"级联剪切"
39     // 否则，则判断是否需要更新堆的最小节点
40     parent = node->parent;
41     if(parent != NULL)
42     {
43         cut(node, parent);
44         cascadingCut(parent);
45     }
46     else if(min == node)
47     {
48         right = node->right;
49         while(right != node)
50         {
51             if(node->key > right->key)
52                 min = right;
53             right = right->right;
54         }
55     }
56 }

    7. 删除节点

    删除节点，本文采用了操作是："取出最小节点"和"减小节点值"的组合。
    (1) 先将被删除节点的键值减少。减少后的值要比"原最小节点的值"即可。
    (2) 接着，取出最小节点即可。

    删除节点值的代码

     1 /*
 2  * 删除结点node
 3  */
 4 template <class T>
 5 void FibHeap<T>::remove(FibNode<T> *node)
 6 {
 7     T m = min->key-1;
 8     decrease(node, m-1);
 9     removeMin();
10 }
  • 相关阅读:
    elasticsearch-5.1.1 安装的问题
    idea 新建New Module时Maven的列表加载不出来
    使用X-Pack插件来进行权限控制
    Groovy学习记录-------Groovy安装/配置
    学习使用Apollo配置中心
    Apollo配置中心介绍
    自定义的GitLab 头像无法正常显示以及URL总是指向localhost
    2020/2/19
    一九八四
    Python 进阶
  • 原文地址：https://www.cnblogs.com/Long-w/p/9788415.html
Copyright © 2011-2022 走看看