存在n个从高到低排布的阶梯
我们只可以从到相邻的低阶梯移动棋子
最低阶梯的棋子就相当于拿走
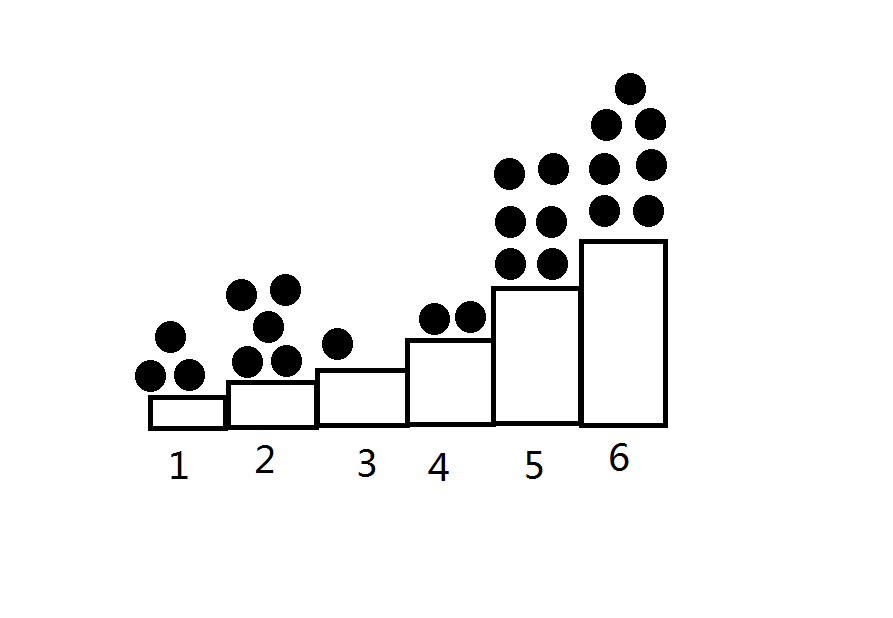
例如
1.我们可以从3到2移动一个棋子
2.我们不可以从4到3移动3个棋子
3.我们可以直接从1阶梯上拿走棋子
结论有些直接
(a_1 xor a_3 xor a_5 xor ...... xor a_{lfloorfrac{n-1}{2} floor*2+1}==0 ?) 后手必胜 : 先手必胜
为什么是这样呢 ? ? ?
讲解
我们从水题【poj1704】当中获得启迪
那么同理
如果当前一方把偶数阶梯石子移动到了奇数阶梯上
那么 对手就可以根据抵消原则 再把多出来的石子 移动到下一阶梯上
那么 最终都只会被移到1上 然后拿走
这样的话实际上产生影响的就是奇数阶梯上的数字
大概需要意会一下
为什么不可以等效为 偶数号 呢 ? ? ?
因为如果当前方把奇数阶梯的石子移动到偶数阶梯上的话
按照规则 对手需要将其移动到下一个偶数阶梯上
但是最终是移动到了2 然后都移动到了1上
但是这不等于游戏结束
如果当前再在将奇数阶梯上的石子移动走 也就是移动到不可以在移动的0阶梯上
那么我们是无法移动然后抵消的
这样的话我们就无法 等价 抵消 然后忽视 奇数阶梯上的石子产生的影响
这相当于破坏原有的Nim而导致胜负关系的不确定