威佐夫博弈
有两堆石子,两个顶尖聪明的人在玩游戏,
每次每个人可以从任意一堆石子中取任意多的石子
或者从两堆石子中取同样多的石子,不能取得人输
分析谁会获得胜利
不想听的的话直接看结论
与前两种博弈不同的是 不可以将两堆石子 分开计算
所以类似需要一个扩展的二维SG
我们定义先手必输的局势就是奇异局势
第一个奇异局势就是((0,0))
((x,y)=(y,x))等价
考虑递推的思想
从直角坐标系考虑$ (0,0)$是奇异局势
那么((0,k),(k,0),(k,k))都是非奇异局势 把TA们划去
再去寻找第一个没有被划过的点 $ (1,2)(2,1) $
同理处理出((3,5),(4,7),(6,10))
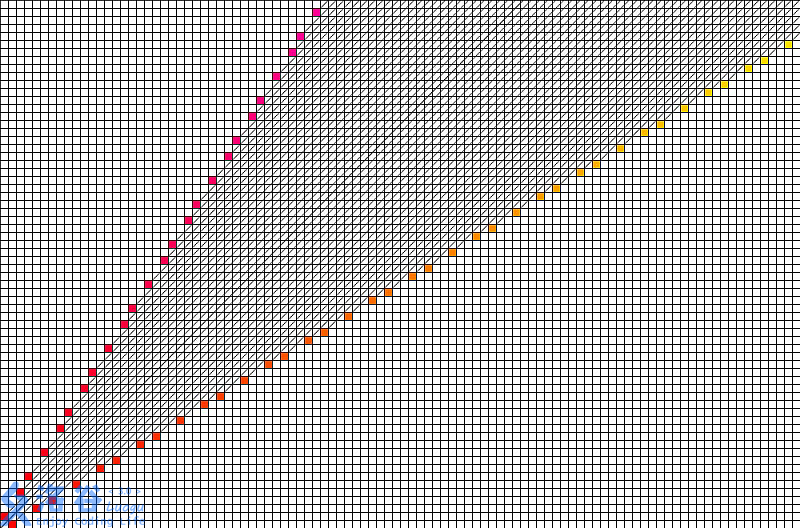
通过大眼观察法 我们find
对于第k个奇异局势$(a_k,b_k)(a_k<b_k) $
1.(a_k)是之前未出现的最小自然数
2.(b_k=a_k+k)
根据我们需找奇异局势的方法 可以证明定理1
使用GH的数学归纳法证明定理2
假定((a_k,a_k+k))是第k个奇异局势
仅需证明((a_{k+1},a_{k+1}+k+1)) 第((k+1))个奇异局势
((a_{k+1},a_{k+1}+k+1))
1.左边取一点
因为(a_i<a_{k+1}(i<k+1) a_i)之前已经出现过
所以左边少了那就把右边拿成对应的情况
2.右边取一点
取得比较少的时候 两队之间差值减小 成为((a_{k+1},a_{k+1}+m))
那么我们就拿成((a_m,a_m+m))
取得比较多的时候 右边<左边
那么右边就是之前出现过的一个(a_i(i<(k+1)))
又因为(a_i+i=b_i<a_{k+1}) 所以可行
那么左边取成类似的情况
3.两边同时取
(a_m,a_m+k+1)因为((k+1)>m) 所以取成$(a_m,a_m+m) $
如上我们可以发现
任意情况下奇异局势都会成为非奇异局势
非奇异局势总是能够成为奇异局势
所以
奇异局势对应必败态
非奇异局势对应必胜态
那么我们仅需要计算出当前
((x,y)(x<y) x)所位于第几个奇异局势
这需要运用到Beatty数列和Beatty定理 不加详述
(a_k=frac {sqrt{5}+1}{2}*k)
$b_k=a_k+k $
有兴趣者自行查看