[Matlab] RANSAC平面拟合例子

RANSAC原理

输入：①数据 ②抽样次数N ③距离阈值t ④数量阈值T
输出：最终估计的模型

程序流程：

1. data ：数据
2. 取样本 ：确定模型参数p所需要的最小数据数n，随机取n个数据作为一个样本J
3. 建模型：根据样本J建立模型Mp(J)。
4. 判断距离：根据模型Mp（J）判断所有数据点到模型的距离。
5. 记录：记录 距离小于t的个数total 和 距离小于t的点的索引。
6. 判断：　若total>数量阈值T ：则用距离小于t的点重新估计模型 重复3-5一次。
　　　　   若total<数量阈值T：则跳出。
7. 记录最大total和此时的模型作为最佳模型。
8. 循环N次。
9.输出

---

函数ransac_fitplane

function [a,b,c,d]=ransac_fitplane(data,N,t,T)
figure;plot3(data(1,:),data(2,:),data(3,:),'o');hold on; % 显示数据
iter = N; %抽样次数N
number = size(data,2); % 总数
maxNum=0;     %符合拟合模型的数据的个数
for i=1:iter %循环次数
     sampleidx = randperm(number); sampleidx =sampleidx(1,1:3);
     sample = data(:,sampleidx); %取样本
     [a1,a2,a3,a4]=get_nice_plane(sample);%拟合直线方程 z=ax+by+c
     plane = [-a1/a3,-a2/a3,-1,-a4/a3];%建模型
     mask=abs(plane*[data; ones(1,size(data,2))]);    %求每个数据到拟合平面的距离
     total=sum(mask<t); %计算数据距离平面小于一定阈值的数据的个数
     index= mask<t;
     if total>T
         nsample=data(:,index);
         [a1,a2,a3,a4]=get_nice_plane(nsample);
         plane = [-a1/a3,-a2/a3,-1,-a4/a3];  %z=ax+by+c
         mask=abs(plane*[data; ones(1,size(data,2))]);
         total=sum(mask<t);              %计算数据距离平面小于一定阈值的数据的个数
     end;
     if total>maxNum   %记录最大total
         maxNum=total;
         bestplane=plane;%最好的拟合平面
         bestindex=index;
         bestplane2=[a1,a2,a3,a4];
    end  
end
%显示符合最佳拟合的数据
maxNum %最大一致集
avgerror=abs(bestplane*[data; ones(1,size(data,2))]);
avgerror=sum(avgerror(find(avgerror<t)))/maxNum  %计算一致集内平均误差
a=bestplane2(1);b=bestplane2(2);c=bestplane2(3);d=bestplane2(4);
% 图形绘制
temp1=data(1,bestindex);
temp2=data(2,bestindex);
xfit = min(temp1):0.2:max(temp1);
yfit = min(temp2):0.2:max(temp2);
[XFIT,YFIT]= meshgrid (xfit,yfit);
ZFIT = bestplane(1)*XFIT+bestplane(2)*YFIT+bestplane(4);
mesh(XFIT,YFIT,ZFIT);grid on;
xlabel('X');
ylabel('Y');
end

函数get_nice_plane

function [a,b,c,d]=get_nice_plane(data)
planeData=data';
% 协方差矩阵的SVD变换中，最小奇异值对应的奇异向量就是平面的方向
xyz0=mean(planeData,1);
centeredPlane=bsxfun(@minus,planeData,xyz0);
[~,~,V]=svd(centeredPlane);
a=V(1,3);
b=V(2,3);
c=V(3,3);
d=-dot([a b c],xyz0);
end　　

主程序

mu=[0 0 0];
S=[2 0 4;0 4 0;4 0 8]; 
data1=mvnrnd(mu,S,400);
%外点
mu=[2 2 2];
S=[8 1 4;1 8 2;4 2 8];
data2=mvnrnd(mu,S,500);
data=[data1',data2'];%% 相当于原始数据
[a,b,c,d]=ransac_fitplane(data,3000,0.5,300)

　　

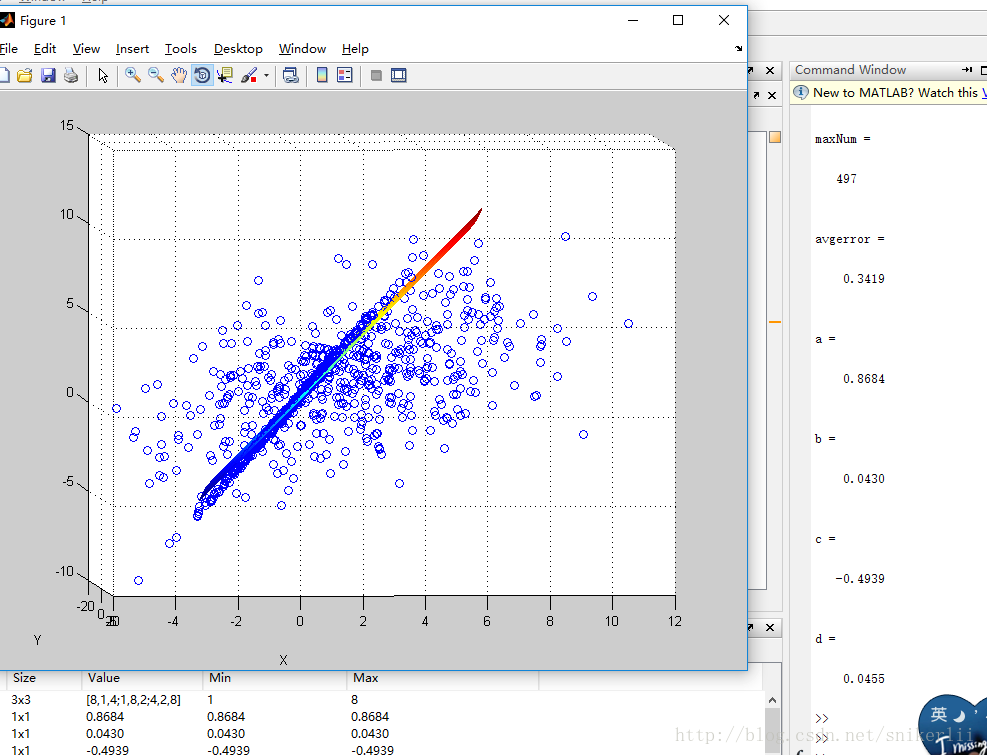
实验结果