//"LinkStack.h" #include<iostream> using namespace std; #define LElemType BiTree #define MAXSIZE 100 typedef struct BiTNode{ char data; struct BiTNode *lchild,*rchild; }BiTNode,*BiTree; typedef struct StackNode{ LElemType data; struct StackNode *next; }StackNode,*LinkStack; string InitStack(LinkStack &S){ S=NULL; return "OK"; } string Push(LinkStack &S,LElemType e){ LinkStack p = new StackNode; p->data = e; p->next=S; S=p; return "OK"; } string Pop(LinkStack &S,LElemType &e){ if(S==NULL) return "ERROR"; e = S->data; LinkStack p = S; S = S->next; delete p; return "OK"; } LElemType GetTop(LinkStack S){ if(S != NULL){ return S->data; } } int StackEmpty(LinkStack S){ if(S == NULL) return 1; else return 0; }
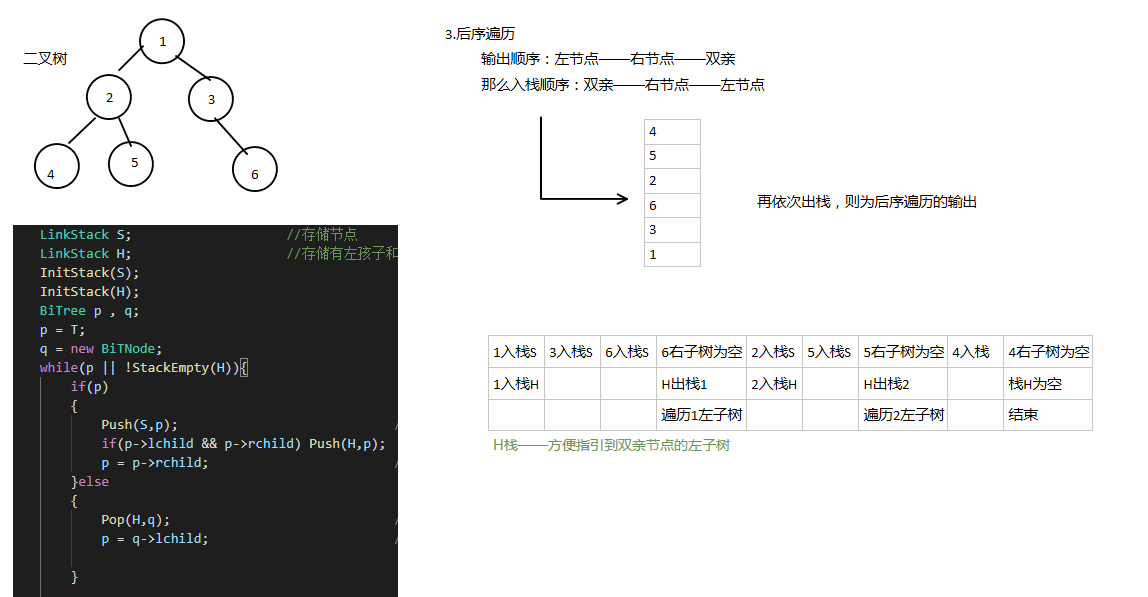
#include <iostream> #include <cmath> #include "LinkStack.h" using namespace std; typedef char TElemType ; // typedef struct BiTNode{ // TElemType data; // struct BiTNode *lchild,*rchild; // }BiTNode,*BiTree; void InitTree(BiTree T){ T->data = {}; T->lchild = NULL; T->rchild = NULL; } void PreOrderTraverse(BiTree T){ if(T){ cout << T->data; PreOrderTraverse(T->lchild); PreOrderTraverse(T->rchild); } } void PreOrderTraverse1(BiTree T){ //先序遍历 LinkStack S; InitStack(S); BiTree p , q; p = T; q = new BiTNode; while(p || !StackEmpty(S)){ if(p) { cout << p->data; //先输出节点,再遍历其左子树 Push(S,p); p = p->lchild; }else { Pop(S,q); p = q->rchild; } } } void InOrderTraverse(BiTree T){ if(T){ InOrderTraverse(T->lchild); cout << T->data; InOrderTraverse(T->rchild); } } void InOrderTraverse1(BiTree T){ //中序遍历 LinkStack S; InitStack(S); BiTree p , q; p = T; q = new BiTNode; while(p || !StackEmpty(S)){ if(p) { Push(S,p); p = p->lchild; //遍历左子树 }else { Pop(S,q); cout << q->data; //输出节点 p = q->rchild; //遍历右子树 } } } void PosOrderTraverse(BiTree T){ if(T){ PosOrderTraverse(T->lchild); PosOrderTraverse(T->rchild); cout << T->data; } } void PosOrderTraverse1(BiTree T){ LinkStack S; //存储节点 LinkStack H; //存储有左孩子和右孩子的节点 InitStack(S); InitStack(H); BiTree p , q; p = T; q = new BiTNode; while(p || !StackEmpty(H)){ if(p) { Push(S,p); //先把节点压入栈 if(p->lchild && p->rchild) Push(H,p); p = p->rchild; //再把右子树节点压入栈 }else { Pop(H,q); //H栈是方便指引到右子树的双亲节点的左子树 p = q->lchild; //最后把左子树节点压入栈 } } while(S){ BiTree a; Pop(S,a); cout << a->data; } } int main(){ BiTree T = new BiTNode; InitTree(T); char ch; int i = 1; int parent; cout << "How many levels in the complete binary tree,# means NULL"<<endl; //输入树的层数, int num,levels; //按完全二叉树的格式顺序输入,#表示空,!表示输入结束 cin >> levels; num = pow(2,levels) -1; BiTree Nodes[num]; cin >> ch; T->data=ch; Nodes[0] = T; cin >> ch; i++; while(ch != '!'){ //二叉树构建 BiTree p =new BiTNode; InitTree(p); if(ch == '#') p = NULL; else p->data = ch; Nodes[i-1] = p; //数组——用于保存双亲节点 parent = i/2; //Nodes[parent],指示第i个节点的双亲 if(parent > 0 && Nodes[parent-1] != NULL){ if(i % 2 == 0) Nodes[parent-1]->lchild = p; else Nodes[parent-1]->rchild = p; } i++; cin >> ch; } PreOrderTraverse(T); cout <<endl; PreOrderTraverse1(T); // InOrderTraverse(T); // cout <<endl; // InOrderTraverse1(T); // PosOrderTraverse(T); // cout <<endl; // PosOrderTraverse1(T); system("pause"); return 0; }

2.对于先序遍历,就在节点入栈前将其输出。
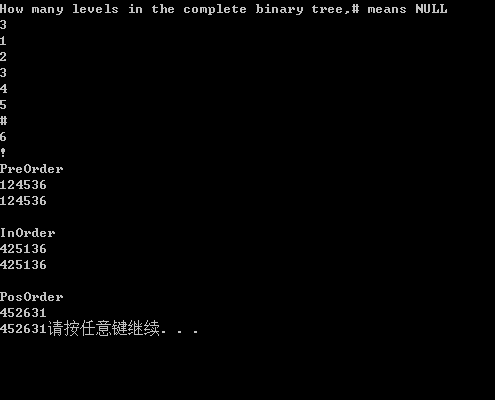
运行截图: