该图片摘自http://blog.csdn.net/qq_33823833/article/details/73881823
输出
0
样例2
输入
3
001
100
010
输出
2
样例3
输入
4
1110
1100
1100
1000
输出
4
分析
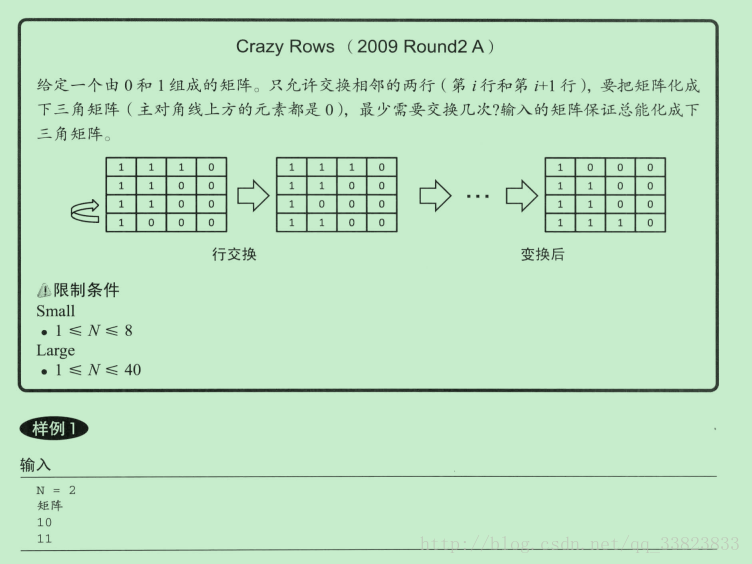
观察三个样例的下三角矩阵会发现,下三角矩阵的每一行的最右边的1的位置不会超过行号,满足这个条件就可以构成下三角矩阵。从第一行开始一个个找下三角矩阵的每一行,从上到下遍历输入的矩阵,一旦找到满足要找的三角矩阵的行,就让它交换到三角矩阵要找的行处,然后再继续从上到下遍历输入的矩阵,找三角矩阵的下一行,这样就可以保证交换的次数最少。
参考代码
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int main()
{
const int INF=1e9;
int N;
char c[41][41];//将矩阵保存到该字符数组
int b[41];//表示第i行的1的最右边的位置
int min=1;
int sum=0;
scanf("%d",&N);
memset(b,0,sizeof(b));
for(int i=0;i<N;i++){
scanf("%s",c[i]);
}
//从每一行后面开始遍历找到每一行最后边的1
for(int i=0;i<N;i++){
for(int j=N-1;j>=0;j--){
if(c[i][j]=='1'){
b[i]=j+1;
j=-1;
};
}
}
while(min<=N){
for(int i=0;i<N;i++){
if(b[i]<=min){
if(i+1==min)
b[i]=INF;
//输入矩阵的i+1行不满足下三角矩阵那么就找到满足的行,交换过来
else{
for(int k=i;k>min-1;k--){
swap(b[k],b[k-1]);
}
b[min-1]=INF;
sum+=i-(min-1);
}
min++;
break;
}
}
}
printf("%d
",sum);
return 0;
}