用于处理不重合由大量节点通过两两相连形成的不重合集合的合并问题。
形成过程详解:
1.一开始所有元素都自成一个集合。
 (图片来自网络)
(图片来自网络)
2.根据连接关系(题目描述或者自行连接)
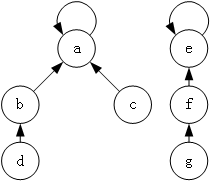
将a,b节点相连,即是将两个节点所在集合合并。合并方式是将集合A通过其根元素连接到集合B根元素并作为其子节点的方式并入集合B。
多次操作后就形成了相关元素各成一体的不重合集合。
 (图片来自网络)
(图片来自网络)
构建方法:构建并查集,就一定能通过任意节点找到其所在集合的根节点。
由此设置
struct Node { int pre; };
Node point[MAXN];
每一个节点内存储了父节点的位置。我习惯用结构体去表示,实际上简单问题是可以用数组来表示父节点的,但是结构体便于添加节点的其他信息。
首先每个节点自成集合,所以初始化为本身。
for(int i=0;i<MAXN;i++) point[i].pre=i;
在得到连接关系后,需要写一个find函数来查找节点所在集合的根节点。
int find(int num) { while(point[num].pre!=num) num=point[num].pre; return num; }
把point[find(a)].pre=point[find(b)];就完成了a,b所在集合的合并。
路径压缩:
在节点合并次数过多时,查找路径会变得越来越长,为了加快查找速度,在每次查找的过程中,都把查到的节点绑定到根节点上。
int find(int num) { int i,j,k; i=num; while(point[i].pre!=i) { i=point[i].pre; } j=num; while(point[j].pre!=j) { k=point[j].pre; point[j].pre=i; j=k; } return i; }
递归版路径压缩:
int Find(int x) { if(pre[x]==x) return x; return pre[x]=Find(pre[x]); }