转:https://blog.csdn.net/tingyun_say/article/details/52343897
讲一个比较有意思的故事:约瑟夫是犹太军队的一个将军,在反抗罗马的起义中,他所率领的军队被击溃,只剩下残余的部队40余人,他们都是宁死不屈的人,所以不愿投降做叛徒。一群人表决说要死,所以用一种策略来先后杀死所有人。
于是约瑟夫建议:每次由其他两人一起杀死一个人,而被杀的人的先后顺序是由抽签决定的,约瑟夫有预谋地抽到了最后一签,在杀了除了他和剩余那个人之外的最后一人,他劝服了另外一个没死的人投降了罗马。
规则是这样的:
在一间房间总共有n个人(下标0~n-1),只能有最后一个人活命。
按照如下规则去杀人:
- 所有人围成一圈
- 顺时针报数,每次报到q的人将被杀掉
- 被杀掉的人将从房间内被移走
- 然后从被杀掉的下一个人重新报数,继续报q,再清除,直到剩余一人
特例:q为2
1. 共有2k个人
我们仔细分析也就是每次除去一半的元素,然后剩余的一半继续重复之前的策略,再除去一半。
得到:j(2^k) = 1
2.共有2k+t个人
例如n = 9时,当除掉一个人之后,就又构成了上一个问题(共有2k个人),这时的第一个是除掉人的后一个。

此时,我们可以把3号看成新的约瑟夫问题中的1号位置:
也就是说这里的1代表的就是上一个问题中的3号
由此递推得出几轮
得到:J(2^k + t) = 2t+1
说完了特例,
现在说说q 不等于2的情况下:
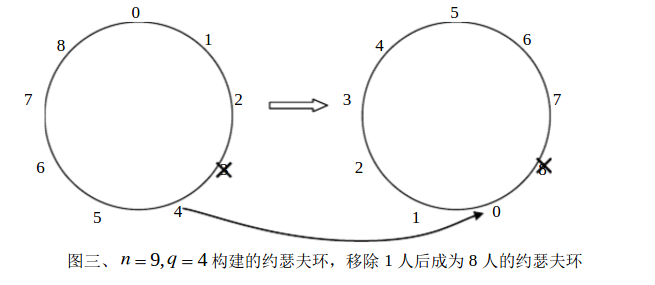
能不能由Jq(n+1)的问题缩小成为J(n)的问题:
现在大概知道我们的新的约瑟夫环的下标都是这样来的:
在旧的下标基础上,减去一个q,再用计算出的结果对长度取余
new = (old-q) % n
反推一下:
old = (new+q) % n
解释的通俗一点就是:人数每次减少一个,最后剩下一个的时候他一定是被杀死的且一定为0,我们要求得是这个0是上一个约瑟夫环中的几号,这样一层一层向上求,求出在当前环中的号数。
代码:
#include<iostream>
#include<stdio.h>
using namespace std;
int yuesefu(int n,int m){
if(n == 1){
return 0; //这里返回下标,从0开始,只有一个元素就是剩余的元素0
}
else{
return (yuesefu(n-1,m) + m) % n; //我们传入的n是总共多少个数
}
}
int main(void){
int a,b;
cin>>a>>b;
cout<<yuesefu(a,b)<<endl;
//或者,直接循环迭代,求出来的result如上
int result = 0;
for(int i = 2;i <= a;i++){
result = (result+b) %i;
}
cout<<"result = "<<result<<endl;
return 0;
}