Describe:
有n项工作,每项工作分别再si时间开始,在ti时间结束;对于每项工作,你都可以参与与否,如果选择参与,那么自始自终都必须全程参与;此外参加工作的时间段不能重复(即使是开始的瞬间和结束的瞬间的重叠也不允许);
你的目标是参与尽可能多的工作,那么最多能参与多少项工作呢?
1<=n<=100000
1<=si<=ti<=10^9
输入:
第一行:n
第二行:n个整数空格隔开,代表n个工作的开始时间
第三行:n个整数空格隔开,代表n个工作的结束时间
样例输入:
5
1 2 4 6 8
3 5 7 9 10
样例输出:
3
Thinking:

最终我们需要将一个个事件按结束时间排序,如何让它们排序并且保证每个事件的开始、结束时间是对应的呢?
这里是将 si 和 ti 作为一个类的成员变量,然后构建对象数组;
#include <iostream>
#include <algorithm>
using namespace std;
class Thing //建立事件类,里面存放事件的起始时间s,终止时间e
{
public:
int s;
int e;
Thing(int ss = 0, int ee = 0) //构造函数
{
s = ss;
e = ee;
}
};
bool compare(Thing a, Thing b)//自定义sort函数的第三个参数--排序函数,因为sort并不能按原有排序函数对类生成的对象进行排序
{
return a.e < b.e; //意思就是 a.e比b.e小 ,a要在b前面
}
int fun(int n, int si[], int ti[])
{
int count = 1;//计数,此处代表第一个事件完成
Thing th[n];
for (int i = 0; i < n; i++) //对类的对象赋值
{
th[i].s = si[i];
th[i].e = ti[i];
}
sort(th, &th[n-1], compare);//sort排序(要排序的数组的起始地址,最后一个要排序的地址,排序函数)
int last = th[0].e;
for (int i = 1; i < n; i++)//依次找跟在上一个事件后的事件(下一件事的开始时间大于上一件事的结束时间)
{
if (th[i].s > last)
{
count++;
last = th[i].e;
}
}
return count;
}
int main()
{
int n = 5;
int si[] = {1, 2, 4, 6, 8};
int ti[] = {4, 3, 7, 9, 10};
cout << fun(n, si, ti);//输出结果为3
return 0;
}
排完序后是这样的(这里没有用样例,因为它本来就是有序的)
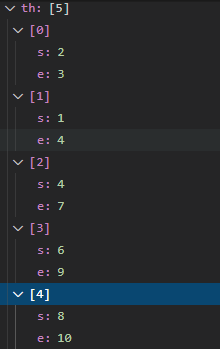
所以以后遇到区间调度问题,应想到按结束时间排序即可得解!
如有错误,感谢指正!