1 需求分析
1.1 银行家算法的实现思想
允许进程动态地申请资源,系统在每次实施资源分配之前,先计算资源分配的安全性,若此次资源分配安全(即资源分配后,系统能按某种顺序来为每个进程分配其所需的资源,直至最大需求,使每个进程都可以顺利地完成),便将资源分配给进程,否则不分配资源,让进程等待。
1.2 死锁的概念
死锁是指两个或两个以上的进程在执行过程中,由于竞争资源或者由于彼此通信而造成的一种阻塞的现象,若无外力作用,它们都将无法推进下去。此时称系统处于死锁状态或系统产生了死锁,这些永远在互相等待的进程称为死锁进程。
银行家算法是避免死锁的一种重要方法。 操作系统按照银行家制定的规则为进程分配资源,当进程首次申请资源时,要测试该进程对资源的最大需求量,如果系统现存的资源可以满足它的最大需求量则按当前的申请量分配资源,否则就推迟分配。当进程在执行中继续申请资源时,先测试该进程已占用的资源数与本次申请的资源数之和是否超过了该进程对资源的最大需求量。若超过则拒绝分配资源,若没有超过则再测试系统现存的资源能否满足该进程尚需的最大资源量,若能满足则按当前的申请量分配资源,否则也要推迟分配。
1.3 产生死锁的必要条件
① 互斥条件:指进程对所分配到的资源进行排它性使用,即在一段时间内某资源只由一个进程占用。如果此时还有其它进程请求资源,则请求者只能等待,直至占有资源的进程用毕释放。
② 请求和保持条件:指进程已经保持至少一个资源,但又提出了新的资源请求,而该资源已被其它进程占有,此时请求进程阻塞,但又对自己已获得的其它资源保持不放。
③ 不剥夺条件:指进程已获得的资源,在未使用完之前,不能被剥夺,只能在使用完时由自己释放。
④ 环路等待条件:指在发生死锁时,必然存在一个进程——资源的环形链,即进程集合{P0,P1,P2,···,Pn}中的P0正在等待一个P1占用的资源;P1正在等待P2占用的资源,……,Pn正在等待已被P0占用的资源。
1.4功能实现
理解了死锁的原因,尤其是产生死锁的四个必要条件,就可以最大可能地避免、预防和解除死锁。所以,在系统设计、进程调度等方面注意如何能够不让这四个必要条件成立,如何确定资源的合理分配算法,避免进程永久占据系统资源。此外,也要防止进程在处于等待状态的情况下占用资源,在系统运行过程中,对进程发出的每一个系统能够满足的资源申请进行动态检查,并根据检查结果决定是否分配资源,若分配后系统可能发生死锁,则不予分配,否则予以分配 。因此,对资源的分配要给予合理的规划。
2 概要设计
2.1数据结构
1) 可利用资源向量Available。这是一个含有m个元素的数组,其中的而每一个元素代表一类可利用资源数目,其初始值是系统中所配置的该类全部可用资源的数目,其数值随该类资源的分配和回收而动态的改变。如果Available[j]=K,则表示系统中现有Rj类资源K个。
2) 最大需求矩阵Max。这是一个n*m的矩阵,它定义了系统中n个进程中的每一个进程对m类资源的最大需求。如果Max[i,j]=K;则表示进程i需要Rj类资源的最大数目为K。
3) 分配矩阵Allocation。这也是一个n*m的矩阵,它定义了系统中每一类资源当前已分配给每一进程的资源数。如果Allocation[i,j]=K,则表示进程i当前已分得Rj类资源的数目为K。
4) 需求矩阵Need。这也是一个n*m的矩阵,用以表示每一个进程尚需的各类资源数。如果Need[i,j]=K,则表示进程i还需要Rj类资源K个,方能完成任务。
上述三个矩阵间存在下述关系:Need[i,j]=Max[i,j]-Allocation[i,j]
2.2 设计思路
第一部分:银行家算法模块
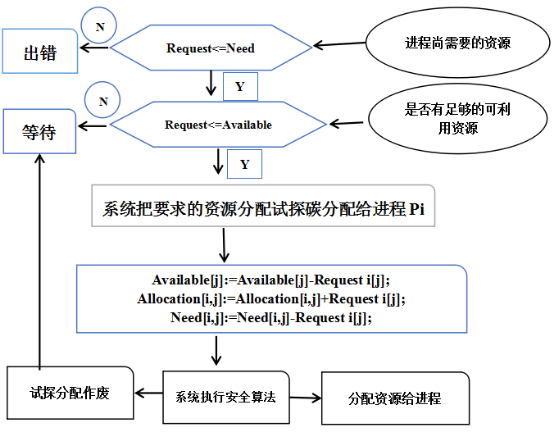
1.如果Request<=Need,则转向2;否则,出错
2.如果Request<=Available,则转向3,否则等待
3.系统试探分配请求的资源给进程
4.系统执行安全性算法
第二部分:安全性算法模块
1. 设置两个向量
① 工作向量:Work=Available(表示系统可提供给进程继续运行所需要的各类资源数目)
② Finish:表示系统是否有足够资源分配给进程(True:有;False:没有).初始化为False
2. 若Finish[i]=False&&Need<=Work,则执行3;否则执行4(i为资源类别)
3. 进程P获得第i类资源,则顺利执行直至完成,并释放资源: Work=Work+Allocation; Finish[i]=true;转2
4. 若所有进程的Finish[i]=true,则表示系统安全;否则,不安全!
3 详细设计
在系统运行过程中,对进程发出的每一个系统能够满足的资源申请进行动态检查,并根据检查结果决定是否分配资源,若分配后系统可能发生死锁,则不予分配,否则予以分配 。因此,对资源的分配要给予合理的规划。
3.1银行家算法
设Request i是进程Pi的申请向量,如果Request i[j]=K,则表示进程Pi需要K个Rj类型的资源。当Pi发出资源请求后,系统按下述步骤进行检查:
1) 如果Request i[j]<=Need[i,j],便转向步骤2);否则认为出错,因为它所需要的资源数已经超过它所宣布的最大值。
2) 如果Request i[j]<=Available[i,j],便转向步骤3);否则,表示尚无足够资源,Pi需等待。
3) 系统试探着把资源分配给进程Pi,并修改下面数据结构中的数值:
Available[j]:=Available[j]-Request i[j];
Allocation[i,j]:=Allocation[i,j]+Request i[j];
Need[i,j]:=Need[i,j]-Request i[j];
4) 系统执行安全性算法,检查此次资源分配后系统是否处于安全状态。若安全,才正式将资源分配给进程Pi,以完成本次分配;否则,将本次的试探分配作废,恢复原来的资源分配状态,让进程Pi等待。
3.2安全性算法
系统所执行的安全性算法可描述如下:
1) 设置两个向量
① 工作向量Work,它表示系统可提供给进程继续运行所需的各类资源数目,它含有m个元素,在执行安全算法开始时,Work:=Available。
② Finish,它表示系统是否有足够的资源分配给进程,使之运行完成。开始时先做Finish[i]:=false;当有足够资源分配给进程时,再令Finish[i]:=ture.
2) 从进程集合中找到一个满足下述条件的进程:
① Finish[i]=false;
② Need[i,j]<=Work[j];若找不到,执行步骤3),否则,执行步骤4)。
3) 当进程Pi获得资源后,可顺利执行,直至完成,并释放出分配给它的资源,故应执行:
Work[j]:=Work[j]+Allocation[i,j];
Finish[i]:=true;
Go to step 2;
4) 如果所有进程的Finish[i]=true都满足,则表示系统处于安全状态;否则,系统处于不安全状态。
3.3流程图
4 测试
4.1结果截图
首先进行初始化:
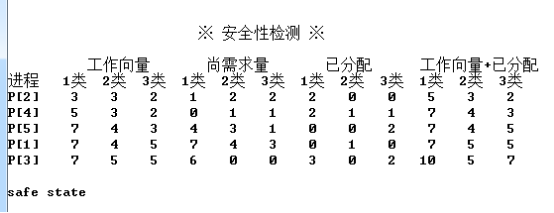
T0时刻进行安全性检测,得到安全序列2->4->5->1->3
T0时刻的资源情况分配图:
P2请求资源,并得到安全序列2->4->5->1->3
P5请求资源:
P1请求资源:
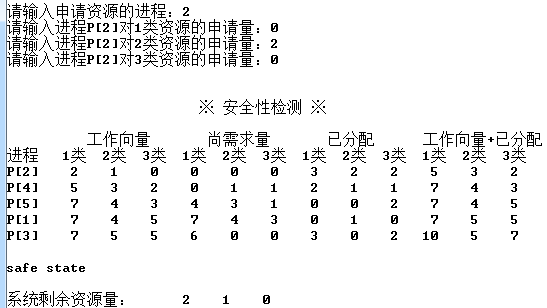
P2请求资源
4.2结果分析
1. T0时刻,利用安全性算法对T0时刻的资源分配情况进行分析,可知,在T0时刻存在着一个安全序列{P[2],P[4],P[5],P[1],P[3]},故系统是安全的。
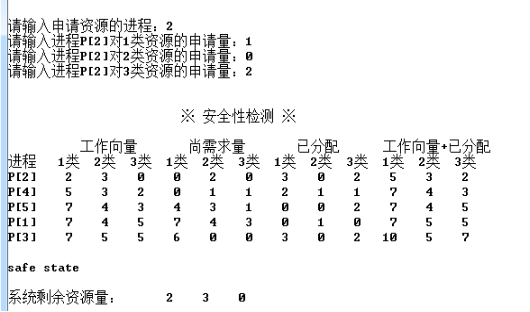
2. P2请求资源:P2发出请求向量Request2(1,0,2),系统按银行家算法进行检查:
① Request 2(1,0,2)<=Need 2(1,2,2,)
② Request 2(1,0,2)<=Available 2(3,3,2)
系统先假定可为P2分配资源,并修改Available,Allocation2和Need2向量,再利用安全性算法检查此时系统是否安全;找到一个安全序列{P[2],P[4],P[5],P[1],P[3]},因此,系统是安全的,可立即将P2所申请的资源分配给它。
3. P5请求资源:P5发出请求向量Request5(3,3,0),系统按照银行家算法进行检查:
① Request 5(3,3,0)<=Need 5(4,3,1)
② Request 5(3,3,0)<=Available 5(2,3,0),让P5等待
4. P1请求资源:P1发出请求向量Request1(0,2,0),系统按照银行家算法进行检查:
① Request 1(0,2,0)<=Need 2(7,4,3)
② Request 1(0,2,0)<=Available 2(2,3,0)
系统先假定可为P0分配资源,并修改数据,进行安全性检查:
可用资源Available(2,1,0)已不能满足任何进程需求,故系统进入不安全状态,此时系统不分配资源。
5. P2请求资源:P2发出请求向量Request2(0,2,0),系统按银行家算法进行检查,可以检测到安全序列。此时进程P2执行完毕,回收P2的已分配资源。
//附录:源代码
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
int Available[10]; //可使用资源向量
int Max[10][10]; //最大需求矩阵
int Allocation[10][10] = { 0 }; //分配矩阵
int Need[10][10] = { 0 }; //需求矩阵
int Work[10]; //工作向量
int Finish[10]; //是否有足够的资源分配,状态标志
int Request[10][10]; //进程申请资源向量
int Pause[10];
int arr[] = { 0 }; //各类资源总数
int List[10];
int i, j;
int n; //系统资源总数
int m; //总的进程数
int a; //当前申请的进程号
int l, e; //计数器
int b = 0, c = 0, f = 0, g; //计数器
int z = 0;
int securitycheck() //安全性检测
{
printf("
");
printf(" ※ 安全性检测 ※
");
if (n == 3)
{
printf(" 工作向量 尚需求量 已分配 工作向量+已分配
进程 ");
for (c = 1; c <= 4; c++)
{
for (j = 1; j <= n; j++)
{
printf(" %d类", j);
}
}
}
if (n == 2)
{
printf(" 工作向量 尚需求量 已分配 工作向量+已分配
进程 ");
for (c = 1; c <= 4; c++)
{
for (j = 1; j <= n; j++)
{
printf(" %d类", j);
}
}
}
for (i = 1; i <= m; i++)
{
Pause[i] = Available[i]; //Pause[i]只是一个暂时寄存的中间变量,为防止在下面安全性检查时修改到Available[i]而代替的一维数组
Finish[i] = false;
}
for (g = 1; g <= m; g++)
{
for (i = 1; i <= m; i++)
{
b = 0; //计数器初始化
Finish[i] == false;
for (j = 1; j <= n; j++)
{
if (Need[i][j] <= Pause[j])
{
b = b + 1;
}
if (Finish[i] == false && b == n)
{
Finish[i] = true;
printf("
P[%d] ", i); //依次输出进程安全序列
for (l = 1; l <= n; l++)
{
printf(" %2d ", Pause[l]);
}
for (j = 1; j <= n; j++)
{
printf(" %2d ", Need[i][j]);
}
for (j = 1; j <= n; j++)
{
//Allocation[i][j]=Pause[j]-Need[i][j];
printf(" %2d ", Allocation[i][j]);
}
for (j = 1; j <= n; j++)
{
printf(" %2d ", Pause[j] + Allocation[i][j]);
}
for (l = 1; l <= n; l++)
{
Pause[l] = Pause[l] + Allocation[i][l];
}
}
}
}
}
printf("
");
for (i = 1; i <= m; i++)
{
if (Finish[i] == true) f = f + 1; //统计Finish[i]==true的个数
}
if (f == m)
{
printf("safe state");
printf("
系统剩余资源量: ");
for (i = 1; i <= n; i++)
{
printf(" %d ", Available[i]);
}
f = 0; //将计数器f重新初始化,为下一次提出新的进程申请做准备
return 1;
}
else
{
printf("unsafe state ");
for (i = 1; i <= n; i++)
{
Available[i] = Available[i] + Request[a][i];
Allocation[a][i] = Allocation[a][i] - Request[a][i];
Need[a][i] = Need[a][i] + Request[a][i];
}
return 0;
}
}
void initialize() //初始化
{
printf("请输入系统的资源种类数:");
scanf("%d", &n);
for (i = 1; i <= n; i++)
{
printf("第%d类资源总数:", i);
scanf("%d", &arr[i]);
}
printf("请输入进程总数:");
scanf("%d", &m);
for (i = 1; i <= m; i++)
{
for (j = 1; j <= n; j++)
{
printf("进程P[%d]对第%d类资源的最大需求量:", i, j);
scanf("%d", &Max[i][j]);
}
}
for (i = 1; i <= m; i++)
{
for (j = 1; j <= n; j++)
{
printf("进程P[%d]对第%d类资源已分配数:", i, j);
scanf("%d", &Allocation[i][j]);
Need[i][j] = Max[i][j] - Allocation[i][j];
}
}
for (i = 1; i <= n; i++)
{
for (j = 1; j <= m; j++)
{
arr[i] -= Allocation[j][i];
}
}
for (i = 1; i <= n; i++)
Available[i] = arr[i];
securitycheck();
}
void mainrequest() //进程申请资源
{
printf("请输入申请资源的进程:");
scanf("%d", &a);
for (i = 1; i <= n; i++)
{
printf("请输入进程P[%d]对%d类资源的申请量:", a, i);
scanf("%d", &Request[a][i]);
if (Request[a][i] > Need[a][i])
{
printf("
出错!进程申请的资源数多于它自己申报的最大需求量
");
return;
}
if (Request[a][i] > Available[i])
{
printf("
P[%d]请求的资源数大于可用资源数,必须等待
", a);
return;
}
}
for (i = 1; i <= n; i++)
{
//以下是试探性分配
Available[i] = Available[i] - Request[a][i];
Allocation[a][i] = Allocation[a][i] + Request[a][i];
Need[a][i] = Need[a][i] - Request[a][i];
}
int ret=securitycheck();
if (ret == 1)
{
int key = 0;
for (j = 1; j <= n; j++)
{
if (Need[a][j] == 0)
{
key++;
}
}
if (key == n)
{
for (j = 1; j <= n; j++)
{
Available[j] += Allocation[a][j];
Allocation[a][j] = 0;
}
}
}
}
void mainshow()
{
printf("
");
if (n == 3)
{
printf(" 已分配 最大需求量 尚需要量
进程");
}
if (n == 2)
{
printf(" 已分配 最大需求 尚需要量
进程");
}
for (i = 1; i <= 3; i++)
{
for (j = 1; j <= n; j++)
{
printf(" %d类", j);
}
}
for (i = 1; i <= m; i++)
{
printf("
P[%d]", i);
for (j = 1; j <= n; j++)
{
printf(" %2d ", Allocation[i][j]);
}
for (j = 1; j <= n; j++)
{
printf(" %2d ", Max[i][j]);
}
for (j = 1; j <= n; j++)
{
printf(" %2d ", Need[i][j]);
}
}
printf("
系统剩余资源量: ");
for (i = 1; i <= n; i++)
{
printf(" %d ", Available[i]);
}
printf("
");
}
void menu()
{
printf("
卐卍※§ 银行家算法 §※卐卍
");
printf("
1:初始化");
printf("
2:进程进行资源申请");
printf("
3:资源分配状态");
printf("
4:退出程序");
printf("
请输入你的选择: ");
}
int main()
{
int key = 0;
printf("
");
while (1)
{
menu();
scanf("%d", &key);
printf("
");
switch (key)
{
case 1:
initialize();
break;
case 2:
mainrequest();
break;
case 3:
mainshow();
break;
case 4:
printf("
谢谢使用
");
printf("
See you next time !
");
system("pause");
return 0;
}
}
system("pause");
return 0;
}