湖南工业大学个人选拔赛第二场 解题报告

A.连续子串和

贪心题，枚举每一个数字作为结束点。保留前i位的前缀和sum[i]，对于第i为结束的合法序列，其值为sum[i]-sum[i-K]，sum[i]-sum[i-K-1]，...，sum[i]-sum[0]，那么我们只需要对每一个 i 保留sum[0]到sum[i-K]的最小值即可。

代码如下：

#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int INF = 0x7fffffff;
int N, K;
int f[1000005];

int solve() {
    int ret = INF+1;
    int Min = INF;
    for (int i = K; i <= N; ++i) {
        Min = min(Min, f[i-K]);
        ret = max(ret, f[i]-Min);
    }
    return ret;
}

int main() {
//    freopen("data.in", "r", stdin);
//    freopen("data.out", "w", stdout);
    while (scanf("%d %d", &N, &K) != EOF) {
        for (int i = 1; i <= N; ++i) {
            scanf("%d", &f[i]);
            f[i] += f[i-1];
        }
        printf("%d\n", solve());
    }
    return 0;    
}

B.谎言

水题，直接做一个取余操作就可以了，也可以把每一位对应的位权先计算出来乘上系数再加起来。

代码如下：

#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <iostream>
using namespace std;

char num[1005];
int mod;

void solve() {
    int t = 0;
    int len = strlen(num);
    for (int i = 0; i < len; ++i) {
        t = t*10 + num[i]-'0';
        t %= mod;
    }
    printf(t ? "%d\n" : "YES\n", t);
}

int main() {
//    freopen("data.in", "r", stdin);
//    freopen("data.out", "w", stdout);
    while (scanf("%s %d", num, &mod) != EOF) {
        solve();
    }
    return 0;    
}

C.费马定理

数学题，由于已经告知费马定理的存在，那么可以证明最小的满足要求的x一定是p-1的因子。可以假设如果x不是p-1的因子的话，那么令p-1=k*x+r，那么有a^(k*x) * a^r % p = 1，显然a^(k*x)%p = 1，而由于a^(p-1) % p = 1，所以a^r % p = 1，而0 < r < x并且x是满足条件最小的值，因此假设不成立。

代码如下：

#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cmath>
using namespace std;

typedef long long LL;
LL MOD;
int a, p;
const int INF = 0x7fffffff;

int _pow(LL a, int b) {
    LL ret = 1;
    while (b) {
        if (b & 1) {
            ret *= a;
            ret    %= MOD;
        }
        a *= a;
        a %= MOD;
        b >>= 1;
    }
    return ret;
}

void solve() {
    p -= 1;
    int ret = INF;
    int LIM = (int)sqrt(double(p));
    for (int i = 1; i <= LIM; ++i) {
        if (p % i == 0) {
            if (_pow(a, i) == 1) {
                ret = min(ret, i);    
            }
            if (_pow(a, p/i) == 1) {
                ret = min(ret, p/i);
            }
        }
    }
    printf("%d\n", ret);
}

int main() {
//    freopen("data.in", "r", stdin);
//    freopen("data.out", "w", stdout);
    while (scanf("%d %d", &a, &p) != EOF) {
        MOD = p;
        solve();    
    }
    return 0;    
}

D.平面划分

推理题：

   

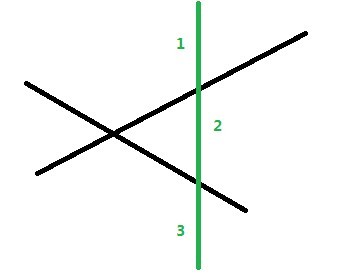
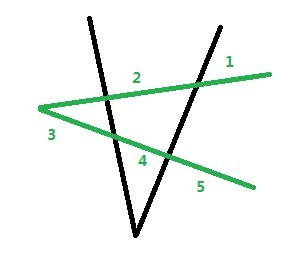
新加入的一条直线与前面的直线都相交能够得到最多的空间划分。考虑到绿色的线是第三根插入的线，那么标号为1,2,3的线就是新区域的边界。对于如图加入第二个V型线，新增5个区域。如果增加第三个椭圆，新增4个区域。最后推出对于直线f[i] = f[i-1] + i；对于V型线f[i] = f[i-1] + 4*i-3；对于椭圆f[i] = f[i] + 2*i-2。

代码如下：

#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <ctime>
using namespace std;

const int MaxN = 1000000;

long long f1[MaxN+5];
long long f2[MaxN+5];
long long f3[MaxN+5];

void pre() {
    f1[1] = f2[1] = f3[1] = 2;
    for (int i = 2; i <= MaxN; ++i) {
        f1[i] = f1[i-1] + i;
    }
    for (int i = 2; i <= MaxN; ++i) {
        f2[i] = f2[i-1] + 4*i-3;
    }
    for (int i = 2; i <= MaxN; ++i) {
        f3[i] = f3[i-1] + 2*i-2;    
    }
}

int main() {
//    clock_t sta = clock();
//    freopen("data.in", "r", stdin);
//    freopen("data.out", "w", stdout);
    int N;
    pre();
    while (scanf("%d", &N) != EOF) {
        printf("%lld %lld %lld\n", f1[N], f2[N], f3[N]);
    }
//    clock_t end = clock();
//    printf("%f\n", 1.0*(end-sta)/1000);
    return 0;
}

E.连续子串和续

利用第一题的做法加上二分搜索。设一个比例参数p，然后就是解决一个ai-p*bi的序列，至少连续K个，sum{ ai-p*bi } >= 0的问题了，二分枚举这个参数即可。

代码如下：

#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

const int INF = 0x7fffffff;
const int MaxN = 1000005;
int N, K;
int A[MaxN], B[MaxN];
double f[MaxN];

bool Ac(double p) {
    double Min = INF;
    f[0] = 0;
    for (int i = 1; i <= N; ++i) {
        f[i] = f[i-1] + A[i]-p*B[i];    
    }
    // 得到seq序列，现在要求一个连续的长度大于K的序列，使得总和大于等于0
    for (int i = K; i <= N; ++i) {
        Min = min(Min, f[i-K]);
        if (f[i] - Min >= 0) {
            return true;
        }
    }
    return false;
}

double bsearch(double l, double r) {
    double mid, ret;
    while (r - l > 1e-8) {
        mid = (l + r) / 2;
        if (Ac(mid)) {
            ret = mid;
            l = mid + 1e-8;
        } else {
            r = mid - 1e-8;    
        }
    }
    return ret;
}

int main() {
//    freopen("data.in", "r", stdin); 
//    freopen("data.out", "w", stdout);
    while (scanf("%d %d", &N, &K) != EOF) {
        for (int i = 1; i <= N; ++i) {
            scanf("%d", &A[i]);
        }
        for (int i = 1; i <= N; ++i) {
            scanf("%d", &B[i]);    
        }
        printf("%.4f\n", bsearch(0, 1000));
    }    
    return 0;
}