Union Find

并查集

并查集 ：

是一种树型的数据结构，常用语处理一些不相交集合的合并及查询问题。

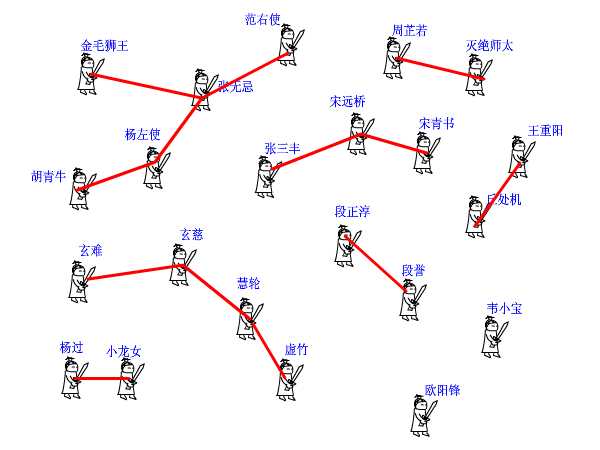
为了解释并查集的原理，我将举一个更有爱的例子。 话说江湖上散落着各式各样的大侠，有上千个之多。他们没有什么正当职业，整天背着剑在外面走来走去，碰到和自己不是一路人的，就免不了要打一架。但大侠们有一个优点就是讲义气，绝对不打自己的朋友。而且他们信奉“朋友的朋友就是我的朋友”，只要是能通过朋友关系串联起来的，不管拐了多少个弯，都认为是自己人。这样一来，江湖上就形成了一个一个的群落，通过两两之间的朋友关系串联起来。而不在同一个群落的人，无论如何都无法通过朋友关系连起来，于是就可以放心往死了打。但是两个原本互不相识的人，如何判断是否属于一个朋友圈呢？

我们可以在每个朋友圈内推举出一个比较有名望的人，作为该圈子的代表人物，这样，每个圈子就可以这样命名“齐达内朋友之队”“罗纳尔多朋友之队”……两人只要互相对一下自己的队长是不是同一个人，就可以确定敌友关系了。

但是还有问题啊，大侠们只知道自己直接的朋友是谁，很多人压根就不认识队长，要判断自己的队长是谁，只能漫无目的的通过朋友的朋友关系问下去：“你是不是队长？你是不是队长？”这样一来，队长面子上挂不住了，而且效率太低，还有可能陷入无限循环中。于是队长下令，重新组队。队内所有人实行分等级制度，形成树状结构，我队长就是根节点，下面分别是二级队员、三级队员。每个人只要记住自己的上级是谁就行了。遇到判断敌友的时候，只要一层层向上问，直到最高层，就可以在短时间内确定队长是谁了。由于我们关心的只是两个人之间是否连通，至于他们是如何连通的，以及每个圈子内部的结构是怎样的，甚至队长是谁，并不重要。所以我们可以放任队长随意重新组队，只要不搞错敌友关系就好了。于是，门派产生了。

              

                                                       

并查集是一种非常简单的数据结构，它主要涉及两个基本操作：

① 合并两个不相交的集合

② 判断两个元素是否属于同一个集合

 

基本操作：

① 合并两个不相交集合_Union(x, y)

　　合并操作很简单：先设置一个数组Father[x],表示x的‘父亲’的编号。那么，合并两个不相交集合的方法就是，找到一个集合的最父亲的父亲（也就是最久远的父亲），将另外一个集合的最久远的父亲的父亲指向他。

 

 

                                                

 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　左图为两个不相交集合，右图为合并后   Father(b) = Father(g)

② 判断两个元素是否属于同一个集合  Find——Set(x)

　　本操作可转化为寻找两个元素的最久远的祖先是否相同、可以采用递归实现。

 

优化：

① Find_Set(x)时，路径压缩

　　寻找祖先时，我们一般采用递归查找，但是当元素很多亦或是整棵树变为一条链时，每次Find_Set(x)都是O(n)的复杂度。为了避免这种情况，我们需要对路径进行压缩，即当我们经过 递归 找到祖先节点后，回溯的时候顺便将他的所有子孙全都直接指向祖先，这样以后再次Find_Set(x) 时复杂度就变成O（1）了，如下图所示，可见路径压缩方便了以后的查找

 

                    

　　　　　　　　                                   　　

 

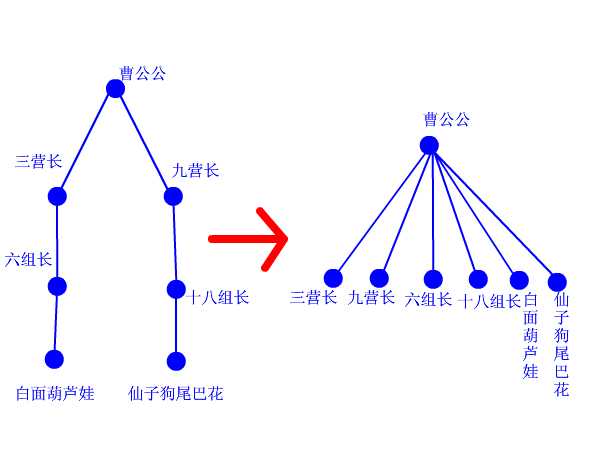
② Union(x, y)时，按秩合并

　　即合并的时候将元素少的集合合并到元素多的集合中，这样合并之后树的高度可能会减少。

 

应用：

并查集常作为另一种复杂的数据结构或者算法的存储结构。常见的应用有：求无向图的连通分量个数，最近公共祖先（LCA），带限制的作业排序，实现Kruskar算法求最小生成树等。

代码：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#define MAX 1024
using namespace std;

int father[MAX];
int rank[MAX];

void Make_Set(int x)
{
    father[x] = x;
    rank[x] = 0;
}

int Find_Set(int x)
{
    if (x != father[x])
    {
        father[x] = Find_Set(father[x]);
    }
    return father[x];
}

void Union(int x, int y)
{
    x = Find_Set(x);
    y = Find_Set(y);
    if (x == y)
        return;
    if (rank[x] > rank[y])
    {
        father[y] = x;
    }
    else
    {
        if (rank[x] == rank[y])
        {
            rank[y]++;
        }
        father[x] = y;
    }
}

int main()
{

}