图基本概念
- 1 顶点
- 2 边(edge)
- 3 路径
- 4 无向图
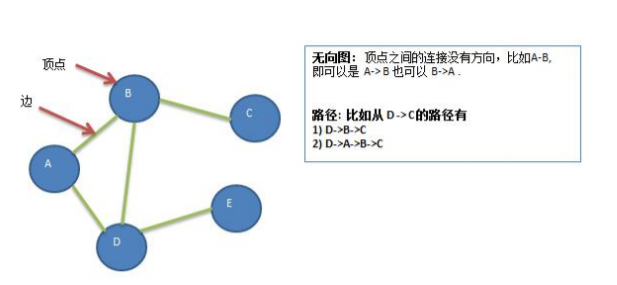
- 5 有向图
- 6 带权图
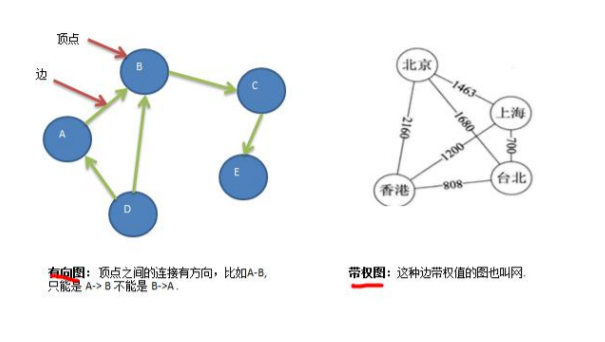
图表示方式
邻接矩阵(二维数组)
- 邻接矩阵是表示图形中顶点之间相邻关系的矩阵,对于n个顶点的图而言,矩阵是的row和col表示的是1....n个点
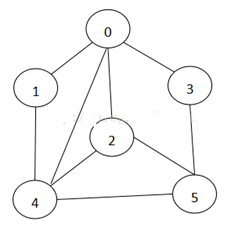

实例图

邻接表(链表)
- 邻接矩阵需要为每个顶点都分配n个边的空间,其实有很多边都是不存在,会造成空间的一定损失.
- 邻接表的实现只关心存在的边,不关心不存在的边。因此没有空间浪费,邻接表由数组+链表组成
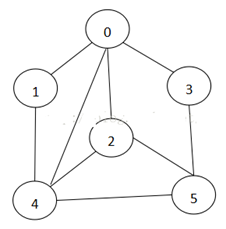
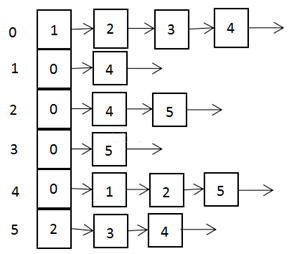
说明:
标号为0的结点的相关联的结点为 1 2 3 4
标号为1的结点的相关联结点为0 4,
标号为2的结点相关联的结点为 0 4 5
图的遍历方式
深度优先遍历DFS)
- 深度优先遍历,从初始访问结点出发,初始访问结点可能有多个邻接结点,深度优先遍历的策略就是首先访问第一个邻接结点,然后再以这个被访问的邻接结点作为初始结点,访问它的第一个邻接结点, 可以这样解:每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。我们可以看到,这样的访问策略是优先往纵向挖掘深入,而不是对一个结点的所有邻接结点进行横向访问。显然,深度优先搜索是一个递归的过程
广度优先遍历(BFS)
- 类似于一个分层搜索的过程,广度优先遍历需要使用一个队列以保持访问过的结点的顺序,以便按这个顺序来访问这些结点的邻接结点
/**
* 图的数据集
*/
private String[] data = null;
/**
* 邻接矩阵
*/
private int[][] edges = null;
/**
* 数据个数
*/
private int size;
private boolean isVisited[] = null;
public AdjacentMatrix(String[] data) {
this.data = data;
this.edges = new int[data.length][data.length];
this.isVisited = new boolean[data.length];
}
public void insertVertex() {
}
public String getValueByIndex(int i) {
return data[i];
}
/**
* @param v1 第几个顶点
* @param v2 相邻的下个节点
*/
public void insertEdge(int v1, int v2) {
insertEdge(v1, v2, 1);
}
/**
* @param v1 第几个顶点
* @param v2 相邻的下个节点
* @param weight 权重
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
size++;
}
/**
* 展示图
*/
public void show() {
for (int[] temp : edges) {
System.out.println(Arrays.toString(temp));
}
}
/**
* 深度优先遍历
*/
public void dfs() {
for (int i = 0; i < isVisited.length; i++) {
if (!isVisited[i]) {
dfs(i);
}
}
System.out.print("尾节点");
}
/**
* @param i 当前处理的数据角标
*/
private void dfs(int i) {
if (!isVisited[i]) {
// 1. 输出当前节点
System.out.print(getValueByIndex(i) + "--->");
// 2. 置为true
isVisited[i] = true;
//3. 查找下个节点
int w = getNextNode(i);
//4. 判断是否存在
while (w != -1) {
// 4.1 没有访问过
if (!isVisited[w]) {
dfs(w);
}
// 4.2 已经访问过 寻找下个节点
w = getJumpNode(i, w);
}
}
}
/**
* @param i 当前节点
* @return 下一个节点
*/
private int getNextNode(int i) {
for (int temp : edges[i]) {
if (temp != 0) {
return temp;
}
}
return -1;
}
/**
* @param i 当前节点
* @param jumpIndex 跳过节点
* @return 下一个节点
*/
private int getJumpNode(int i, int jumpIndex) {
for (int j = jumpIndex + 1; j < data.length; j++) {
if (edges[i][j] > 0) {
return j;
}
}
return -1;
}
/**
* 广度优先遍历
*/
public void bfs() {
for (int i = 0; i < isVisited.length; i++) {
if (!isVisited[i]) {
bfs(i);
}
}
bfs(0);
System.out.print("尾节点");
}
/**
* 广度优先遍历
*/
public void bfs(int i) {
// 1.队列 记录结点访问的顺序
LinkedList<Integer> queue = new LinkedList();
// 2.访问结点,输出结点信息
System.out.print(getValueByIndex(i) + "===>");
// 3.标记为以访问
isVisited[i] = true;
// 4. 将结点加入队列
queue.addLast(i);
while (!queue.isEmpty()) {
// 5. 取出队列头结点的下标
int u = queue.removeFirst();
// 6. 第一个相邻的结点的下标 w
int w = getNextNode(u);
while (w != -1) {
// 7. w 没有访问过
if (!isVisited[w]) {
System.out.print(getValueByIndex(w) + "===>");
// 7.1 标记已经访问
isVisited[w] = true;
// 7.2 入队
queue.addLast(w);
}
// 以u 为前驱结点,找到w后面的下一个邻结点(广度优先的体现)
w = getJumpNode(u, w);
}
}
}