SPCArt算法,利用旋转(正交变换更为恰当,因为没有体现出旋转这个过程),交替迭代求解sparse PCA。
对以往一些SPCA算法复杂度的总结

注:(r)是选取的主成分数目,(m)为迭代次数,(p)为样本维度,(n)为样本数目。本文算法,需要先进行SVD,并未在上表中给出。
Notation

论文概述
(A = USigma V^{mathrm{T}})
(V_{1:r}=[V_1,V_2,ldots, V_r] in mathbb{R}^{p imes r})就是普通PCA的前(r)个载荷向量(loadings,按照特征值降序排列)
(forall 旋转矩阵(正交矩阵)R in mathbb{R}^{r imes r})
(V_{1:r}R)也是彼此正交的,张成同一子空间的向量组。
原始问题
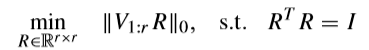
如果能解出来,当然好,可是这是一个很难求解的问题,所以需要改进。
问题的变种
(V_{1:r})直接用(V)表示了,为了符号的简洁。
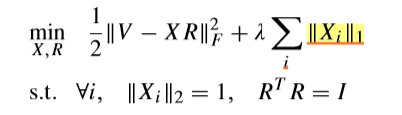
变成这个问题之后,我们所追求的便是(X)了,(X_i),就是我们要的载荷向量,显然,这个问题所传达出来的含义是:
1.我们希望(XR)与(V)相差不大,意味着(X_i)近似正交且张成同一个子空间。
2.(|X_i|_1)作为惩罚项,可以起到稀疏化的作用(这是1-范数的特点)。
算法

这是一个交替迭代算法,我们来分别讨论。
固定(X),计算(R)
当固定(X),之后,问题就退化为:
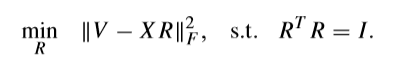
这个问题在Sparse Principal Component Analysis(Zou 06)这篇论文里面也有提到。
上述最小化问题,可以变换为
(max quad tr(V^{mathrm{T}}XR), quad s.t. quad R^{mathrm{T}}R=I)
若(X^{mathrm{T}}V=WDQ^{mathrm{T}})
就是要最大化:
(tr(QDW^{mathrm{T}}R)=tr(DW^{mathrm{T}}RQ)leq tr(D))
当(R = WQ^{mathrm{T}})(注意(W^{mathrm{T}}RQ)是正交矩阵)。
固定(R),求解(X) ((Z =VR^{mathrm{T}}))
1-范数
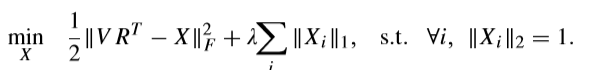
注意:(|VR^{mathrm{T}}-X|_F^2=|(V-XR)R^{mathrm{T}}|_F^2),所以这个问题和原始问题是等价的。
经过转换,上述问题还等价于:
(max_{X_i} quad Z_i^{mathrm{T}}X_i-lambda|X_i|_1 quad i=1,2,ldots,r)
通过分析(蛮简单的,但是不好表述),可以得到:
(X_i^*=S_lambda(Z_i)/|S_lambda(Z_i)|_2)
(T-ell_0)(新的初始问题)
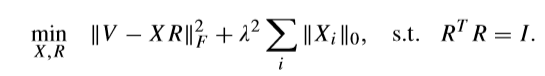
(R)的求解问题没有变化,考虑(R)固定的时候,求解(X)。
等价于:
(mathop{min}limits_{X_{ij},Z_{ij}} quad (Z_{ij}-X_{ij})^2+lambda^2|X_{ij}|_0)
显然,若(X_{ij}^*
eq 0),(X_{ij}^*=Z_{ij}),此时函数值为(lambda^2)
若(X_{ij}^* = 0),值为(Z_{ij}^2),所以,为了最小化值,取:
(min {Z_{ij}^2,lambda^2}),也就是说,
(X_{ij}=0 quad if:Z_{ij}^2>lambda^2) 否则, (X_{ij}=Z_{ij})
(X_i^*=H_lambda(Z_i)/|H_lambda(Z_i)|_2)
T-sp 考虑稀疏度的初始问题
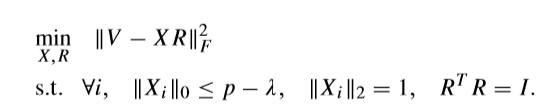
(lambda in {0, 1, 2,ldots,p-1})
(R)的求法如出一辙,依旧只需考虑在(R)固定的情况下,如何求解(X)的情况。
等价于:
(max quad Z_i^{mathrm{T}}X_i) 在条件不变的情况下。
证明挺简单的,但不好表述,就此别过吧。
最优解是:(X_i^*=P_lambda(Z_i)/|P_lambda(Z_i)|_2)
T-en 考虑Energy的问题
(X_i = E_lambda(Z_i)/|E_lambda(Z_i)|_2)
文章到此并没有结束,还提及了一些衡量算法优劣的指标,但是这里就不提了。大体的思想就在上面,我认为这篇论文好在,能够把各种截断方法和实际优化问题结合在一起,很不错。
代码
def Compute_R(X, V):
W, D, Q_T = np.linalg.svd(X.T @ V)
return W @ Q_T
def T_S(V, R, k): #k in [0,1)
Z = V @ R.T
sign = np.where(Z < 0, -1, 1)
truncate = np.where(np.abs(Z) - k < 0, 0, np.abs(Z) - k)
X = sign * truncate
X = X / np.sqrt((np.sum(X ** 2, 0)))
return X
def T_H(V, R, k): #k in [0,1) 没有测试过这个函数
Z = V @ R.T
X = np.where(np.abs(Z) > k, Z, 0)
X = X / np.sqrt((np.sum(X ** 2, 0)))
return X
def T_P(V, R, k): #k belongs to {0, 1, 2, ..., (p-1)} 没有测试过这个函数
Z = V @ R.T
Z[np.argsort(np.abs(Z), 0)[:k], np.arange(Z.shape[1])] = 0
X = Z / np.sqrt((np.sum(Z ** 2, 0)))
return X
def Main(C, r, Max_iter, k): #用T_S截断 可以用F范数判断是否收敛,为了简单直接限定次数
value, V_T = np.linalg.eig(C)
V = V_T[:r].T
R = np.eye(r)
while Max_iter > 0:
Max_iter -= 1
X = T_S(V, R, k)
R = Compute_R(X, V)
return X.T
结果,稀疏的程度大点,反而效果还好点。