引
PPCA 通过高斯过程给出了普通PCA一个概率解释,这是很有意义的。论文还利用PPCA进行缺失数据等方面的处理(不过这方面主要归功于高斯过程吧)。
其中(t in mathbb{R}^d)为观测变量,也就是样本,而(x in mathbb{R}^q)是隐变量,(W in mathbb{R}^{d imes q})将(x,t)二者联系起来。另外,(epsilon)是噪声。
令(S = frac{1}{N} sum limits_{n=1}^N (t_n -mu )(t_n - mu)^T)是样本协方差矩阵,其中(mu)是样本均值。论文的主要工作,就是将(S)的列空间和(W)联系起来。
主要内容
假设(epsilon sim N(0, sigma^2 I)),(: x sim N(0, I)),二者独立。那么,容易知道(t)在(x)已知的情况下的条件概率为:
然后论文指出,通过其可求得(t)的边际分布:
其中(C = WW^T + sigma^2 I)。这个证明,在贝叶斯优化中有提过,不过我发现,因为(t=Wx+mu + epsilon),是服从正态分布随机变量的线性组合,所以(t)也服从正态分布,所以通过(E(t))和(E((t-E(t))(t-E(t))^T))也可以得到(t)的分布。
其似然函数(L)为:
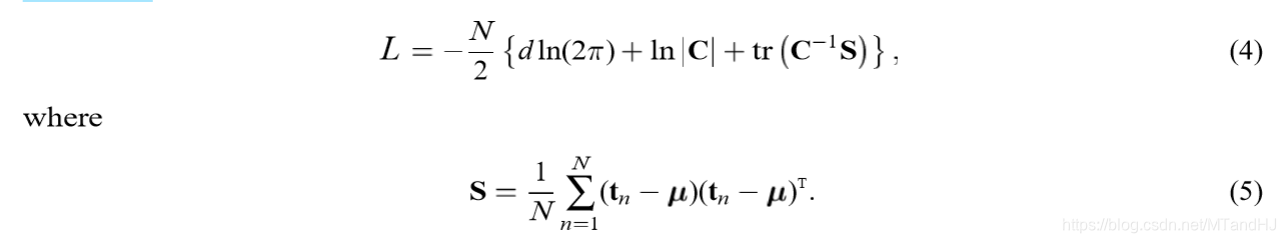
将(W,sigma)视为参数,我们可以得到其极大似然估计:
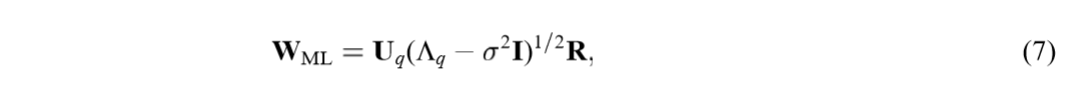
其中(U_{q})的列是(S)的主特征向量,而(Lambda_q)的对角线元素为特征向量对应的特征值(lambda_1, ldots, lambda_q)(为所有特征值的前(q)个,否则(W)将成为鞍点),(R in mathbb{R}^{q imes q})是一个旋转矩阵。注意到,(W_{ML})的列向量并不一定正交。

这部分的推导见附录。
同样的,我们可以推导出,(x)在(t)已知的情况下的条件分布:
其中(M = W^TW+sigma^2I)
这个推导需要利用贝叶斯公式:
为什么要提及这个东西,因为可以引出一个很有趣的性质,注意到(x|t)的均值为:
令(W = W_{ML}),且假设(sigma^2 ightarrow 0),那么均值就成为:
实际上就是((t-u))在主成分载荷向量上的正交投影,当然这里不要计较(W_{ML}^TW_{ML})是否可逆。这就又将PPCA与普通的PCA联系在了一起。
EM算法求解
论文给出了(W)的显式解(虽然有点地方不是很明白),也给出了如何利用EM算法来求解。
构造似然估计:

对(x_n)求条件期望(条件概率为(p(x_n|t_n,W,sigma^2))):
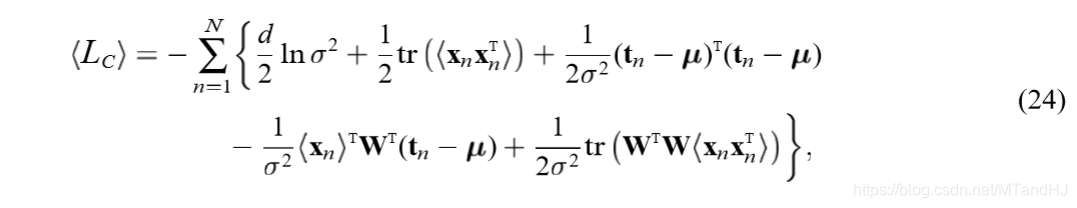
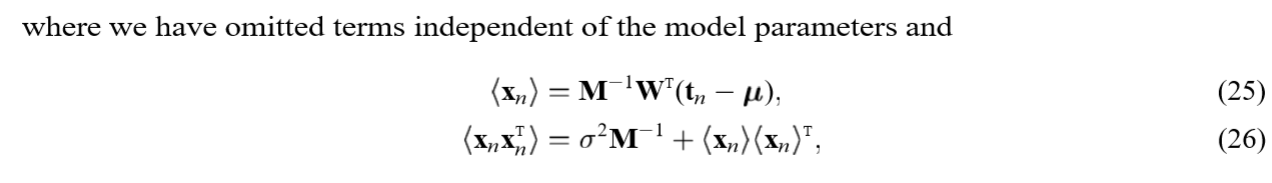
(M)步是对上述(W,sigma)求极大值,注意(<cdot>)里面的(M, sigma)是已知的(实际上,用(M', sigma')来表述更加合适):
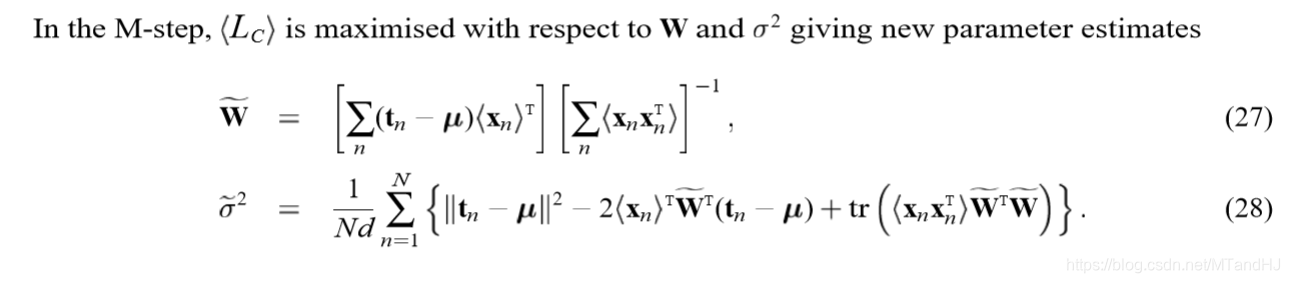
有更加简练的表述形式:
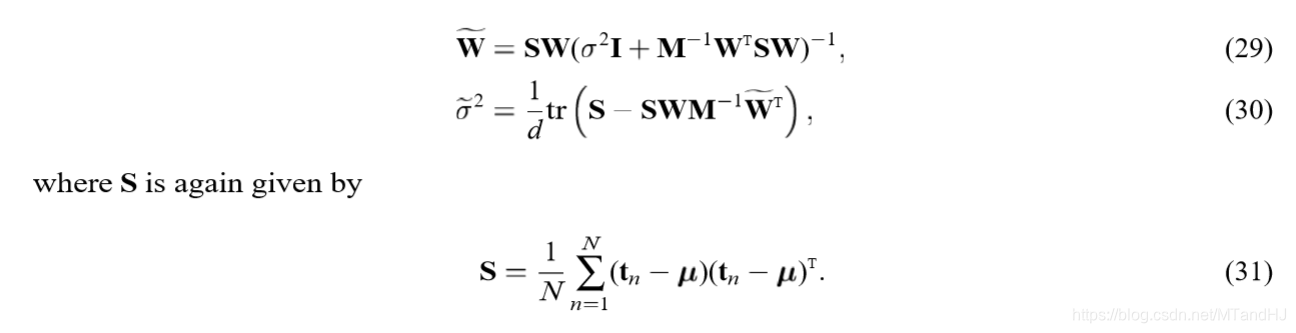
符号虽然多,但是推导并不麻烦,自己推导的时候并没有花多大工夫。
附录
极大似然估计
已知对数似然函数为:
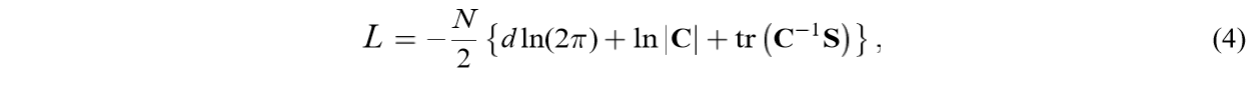
先考察对(W)的微分:
所以,要想取得极值,需满足:
论文说这个方程有三种解:
- (W=0),0解,此时对数似然函数取得最小值(虽然我没看出来)。
- (C=S):
其解为:
其中(S = U_S Lambda U_S^T)。
- 第三种,也是最有趣的解,(SC^{-1}W=W)但是(W e 0, C e S)。假设(W=ULV^T),其中(U in mathbb{R}^{d imes q}), (L in mathbb{R}^{q imes q})为对角矩阵,(V in mathbb{R}^{q imes q})。通过一系列的变换(我没有把握能完成这部分证明,感觉好像是对的),可以得到:
于是(Su_j = (sigma^2I + l_j^2)u_j),其中(u_j)为(U)的第j列,(l_j)为(L)的第j个对角线元素。因此,(u_j)就成了(S)的对应特征值(lambda_j = sigma^2 + l_j^2)的特征向量(注意到这个特征值是必须大于等于(sigma^2))。于是,有:
其中:
实际上就是(k_j=lambda_j)
注意,上面的分析只能说明其为驻定解,事实上(U_q)只说明了其为(S)的特征向量,而没有限定是哪些特征向量。
将解(W = U_q(K_q-sigma^2I)^{1/2}R)代入对数似然函数可得((C = WW^T+sigma^2 I)):
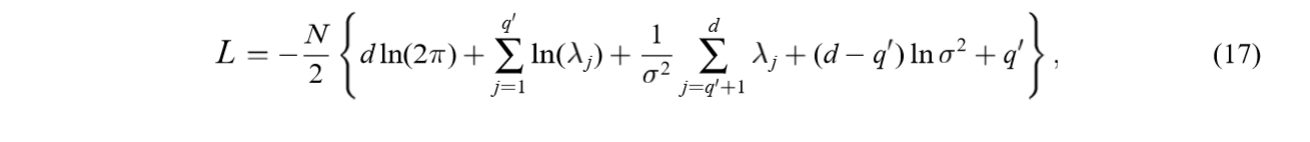
其中(q')是非零(l_1,ldots,l_{q'})的个数。
上面的是蛮好证明的,注意({cdot})中第2项和第4项和为(ln |C|),第3,5项构成(mathrm{tr}(C^{-1}S))。
对(sigma)求极值,可得:
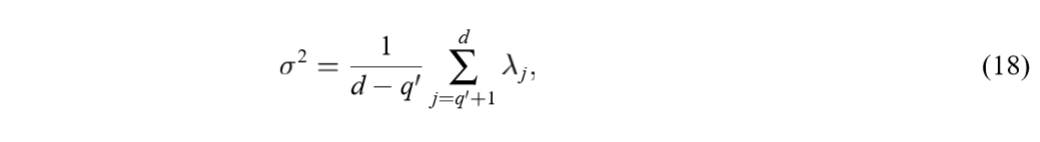
且是极大值,因为显然(sigma
ightarrow 0)会导致(L
ightarrow - infty)。代入原式可得:
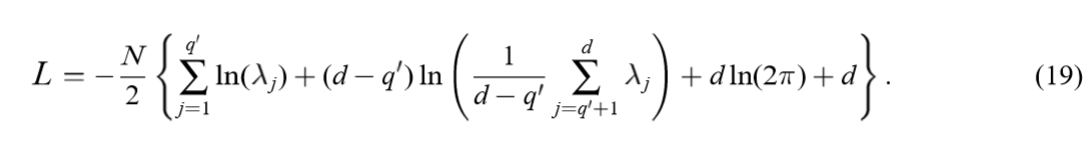
最大化上式等价于最小化下式:
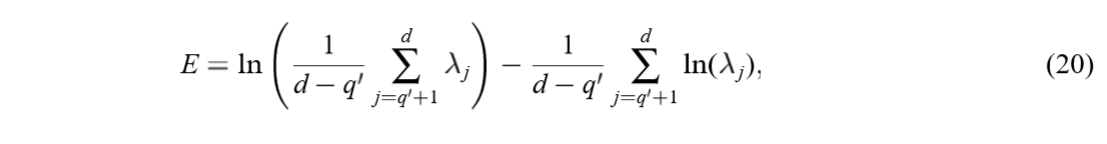
注意到,上式只与被舍弃的(l_j=0)的(lambda_j)有关,又(lambda_i ge sigma^2, i=1,ldots, q),再结合(18),可以知道最小的特征值一定是被舍弃的。但是论文说,应当是最小的(d-q')个特征值作为被舍弃的(因为这些特征值必须在一块?)。

仔细想来,似然函数可以写成:
好吧,还是不知道该如何证明。
代码
"""
瞎写的,测试结果很诡异啊
"""
import numpy as np
class PPCA:
def __init__(self, data, q):
self.__data = np.array(data, dtype=float)
self.__n, self.__p = data.shape
self.__mean = np.mean(self.data, 0)
self.q = q
assert q < self.__p, "Invalid q"
@property
def data(self):
return self.__data
@property
def n(self):
return self.__n
@property
def p(self):
return self.__p
def explicit(self):
data = self.data - self.__mean
S = data.T @ data / self.n
value, vector = np.linalg.eig(S)
U = vector[:, :self.q]
sigma = np.mean(value[self.q:])
newvalue = value[:self.q] - sigma
return U * newvalue
def EM(self):
data = self.data - self.__mean
S = data.T @ data / self.n
W_old = np.random.randn(self.p, self.q)
sigma = np.random.randn()
count = 0
while True:
count += 1
M = W_old.T @ W_old + sigma
M_inv = np.linalg.inv(M)
W_new = S @ W_old @ np.linalg.inv(sigma + M_inv @ W_old.T @ S @ W_old)
sigma_new = np.trace(S - S @ W_old @ M_inv @ W_new.T) / self.p
if np.sum(np.abs(W_new - W_old)) / np.sum(np.abs(W_old)) < 1e-13 and
np.abs(sigma_new - sigma) < 1e-13:
return W_new
else:
W_old = W_new
sigma = sigma_new