Robust De-noising by Kernel PCA

目录

• 引
• 主要内容

Takahashi T, Kurita T. Robust De-noising by Kernel PCA[C]. international conference on artificial neural networks, 2002: 739-744.

引

这篇文章是基于对Kernel PCA and De-Noisingin Feature Spaces的一个改进。

针对高斯核：

[k(x,y) = exp (-|x-y|^2/c) ]

我们希望最小化下式（以找到(x)的一个近似的原像):

[ ho(z) = |Phi(z) - P_H Phi(x)|^2 ]

获得了一个迭代公式：

[z(t) = frac{sum_{i=1}^N w_i k(x_i, z(t-1))x_i}{sum_{i=1}^N w_i k(x_i, z(t-1))} ]

其中(w_i=sum_{h=1}^Hy_h u_i^h),(u)通过求解kernel PCA获得（通常是用(alpha)表示的）,(z(0)=x)。

主要内容

虽然我们可以通过撇去小特征值对应的方向，但是这对于去噪并不足够。Kernel PCA and De-Noisingin Feature Spaces中所提到的方法，也就是上面的那个迭代的公式，也没有很好地解决这个问题。既然({y_h})并没有改变——也就是说，我们可能一直在试图用带噪声的数据去恢复一个不带噪声的数据。

所以，作者论文，在迭代更新过程中，(y_h)也应该进行更新。

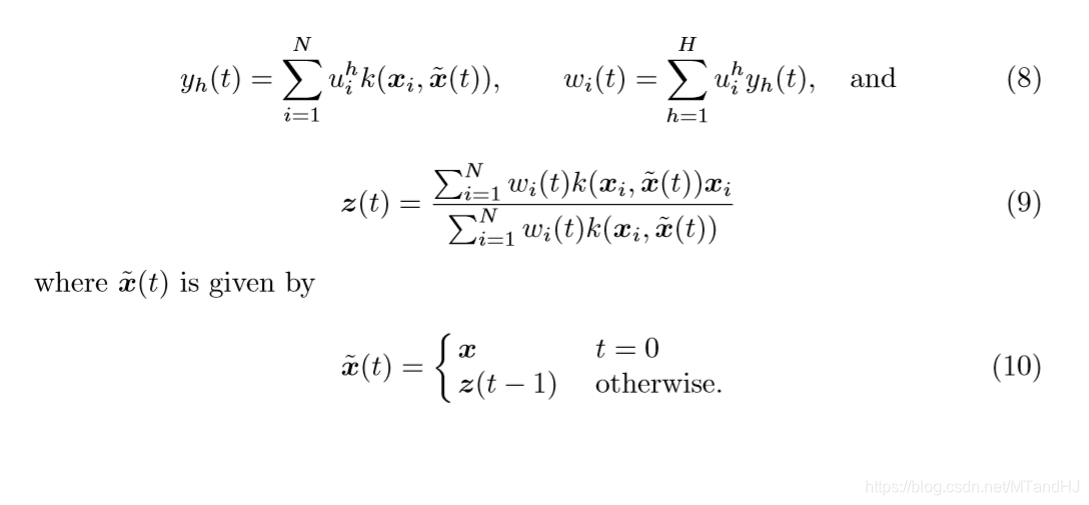
这样，每一步我们都可以看作是在寻找：

[|Phi(z)-P_HPhi(widetilde{x}(t)| ]

的最小值。
从((10))可以发现，除非(widetilde{x}(t)=z(t-1))是(x)的一个比较好的估计，否则，通过这种方式很有可能会失败（这里的失败定义为，最后的结果与(x)差距甚远)。这种情况我估计是很容易发生的。所以，作者提出了一种新的，更新(widetilde{x}(t))的公式：

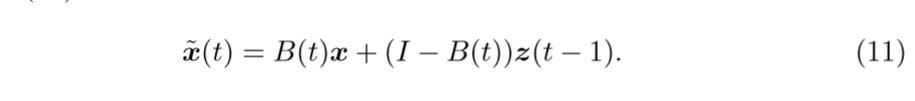
其中(B(t))为确定度，是一个(M imes M)的矩阵，定义为：

[B(t) = diag(eta_1(t), ldots, eta_M(t)) \ eta_j(t) = exp (-(x_j - z_j (t-1))^2/2sigma_j^2) ]

对角线元素，反映了(x_j)和(z_j(t-1))的差距，如果二者差距不大，说明(P_H(x))和(x)的差距不大，(x)不是异常值点，所以，结果和(x)的差距也不会太大，否则(x)会被判定为一个异常值点，自然(z)应该和(x)的差别大一点。

(sigma_j)的估计是根据另一篇论文来的，这里只给出估计的公式：

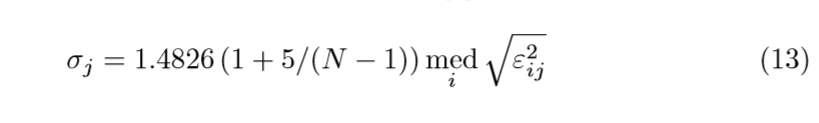
(mathrm{med}(x))表示(x)的中位数，(varepsilon_{ij})表示第(i)个训练样本第(j)个分量与其重构之间平方误差。话说，这个重构如何获得呢？