定义
令(f: mathrm{R}^n ightarrow mathrm{R} cup {+ infty })为闭的凸函数,即其上镜图:
为非空闭的凸集,定义域:
近端算子(是这么翻译的?)proximal operator (mathbf{prox}_f: mathrm{R}^n
ightarrow mathrm{R}^n)定义为:
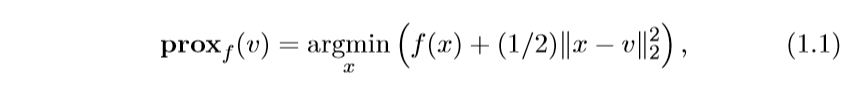
我们常常会对添加一个比例系数(lambda),而关心(lambda f)的近端算子:
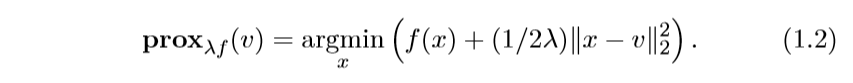
注:等式右边乘以一个常数(lambda)便是(lambda f)的形式,所以是等价的。
解释
图形解释
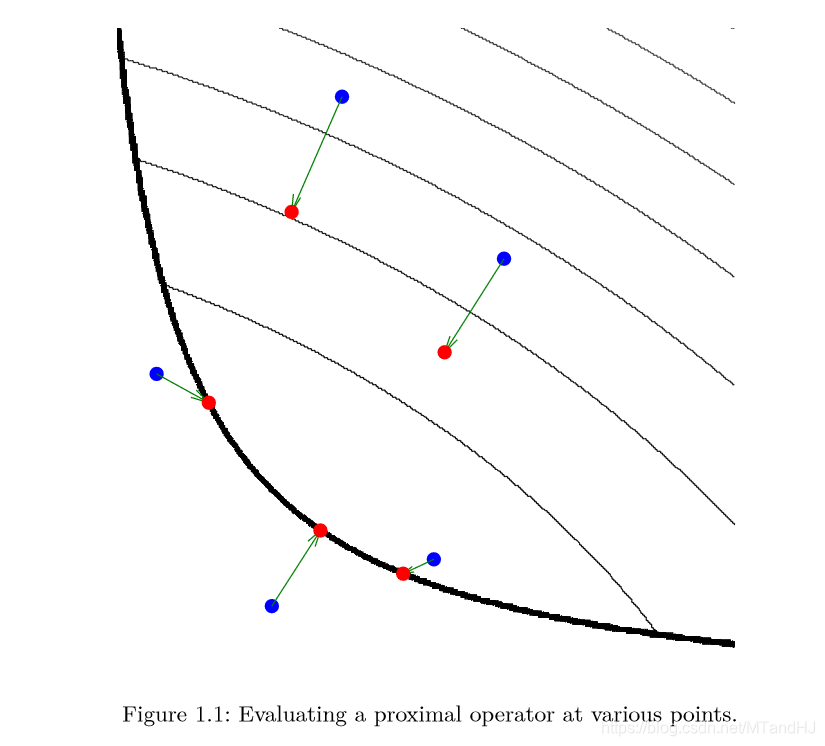
注:图中的细黑线是函数(f)的等值线,而粗黑线表示定义域的边界。在蓝色的点处估计其(mathbf{prox}_f)得到红色的点。
可以发现,(mathbf{prox}_f(v))实际上是对点(v)附近的一个估计。
梯度解释
假设(lambda)很小,且(f)可微,那么,容易知道(f(x) + frac{1}{2lambda}|x-v|_2^2)取得极值(实际上也是最值)的条件是:
可以看到,(mathbf{prox}_f(v))近似为在(v)点的梯度下降,而(lambda)为步长。
一个简单的例子
有一个问题,就是,如果我们的目的是最小化(f(x)),那么利用(mathbf{prox}_f)会不会太愚蠢了,既然我们能求解(mathbf{prox}_f),那么直接最小化(f(x))应该也不是难事吧。这个问题留到以后再讨论吧,我也不知道能否找到一个恰当的例子来反驳。
当(f)是一个示性函数:
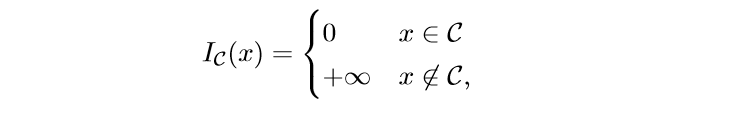
其中(mathcal{C})为非空凸集,我们来看看这个时候的(mathbf{prox}_f(v)):
首先,我们可以确定(x in mathcal{C}), 否则结果为无穷,所以,问题可以转化为一个Euclid范数下投影问题:
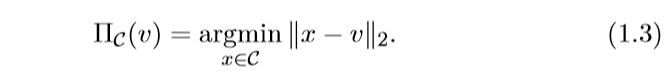
所以一个问题是,如果(mathbf{prox}_f)的尾项不用(ell_2)范数,用别的范数会变成什么样?