Spurious Local Minima are Common in Two-Layer ReLU Neural Networks

目录

• 引
• 主要内容
  • 定理1
  • 推论1
  • 引理1 引理2

Safran I, Shamir O. Spurious Local Minima are Common in Two-Layer ReLU Neural Networks[J]. arXiv: Learning, 2017.

@article{safran2017spurious,
title={Spurious Local Minima are Common in Two-Layer ReLU Neural Networks},
author={Safran, Itay and Shamir, Ohad},
journal={arXiv: Learning},
year={2017}}

引

文章的论证部分让人头疼，仅在这里介绍一下主要内容. 这篇文章关注的是单个隐层, 激活函数为ReLU的神经网络, 且对输入数据有特殊的限制, 数据为:

[sum_{i=1}^k [mathbf{v}_i^Tmathbf{x}]_+, ]

其中(mathbf{v}_i)是给定的, 而(mathbf{x} sim mathcal{N}(mathbf{0}, mathbf{I})). 而这篇文章考虑的是:

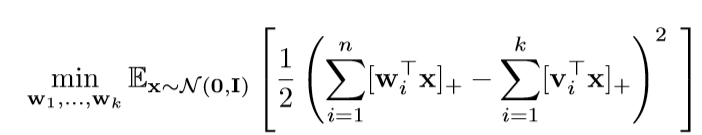
即, 这个损失函数是否具有局部最优解.

主要内容

定理1

注意, (mathbf{v}_1, mathbf{v}_2, ldots, mathbf{v}_k)是正交的, 且(n=k). 这个时候，损失函数是有局部最优解的, 不过在后面作者提到, 如果(n>k), 即overparameter的情况, 这个情况是大大优化的, 甚至出现没有局部最优解(不过是通过实验说明的).

推论1

引理1 引理2

这部分有些符号没有给出, 如果感兴趣回看论文, 这俩个引理是用来说明, 如何在实验中, 通过一些指标来判断是否收敛到某个极值点了(当然, 这需要特别的计算机制来避免舍入误差带来的影响, 作者似乎是通过Matlab里的一个包实现的).