Neal R. M. , MCMC Using Hamiltonian Dynamics[J]. arXiv: Computation, 2011: 139-188.
@article{neal2011mcmc,
title={MCMC Using Hamiltonian Dynamics},
author={Neal, Radford M},
journal={arXiv: Computation},
pages={139--188},
year={2011}}
算法
先把算法列一下.
Input: 初始值(q), 步长(epsilon)与leapfrog迭代次数(L).
- 令(q^{(0)} = q);
- 循环迭代直到停止条件满足(以下第(t)步):
- 从标准正态分布中抽取(p), (q = q^{{(t-1)}}), (p^{(t-1)} = p).
- 重复 (i=1,2,ldots, L):
如果(i ot = L):
- 计算接受概率
- 从均匀分布(U(0,1))中抽取(u), 如果(u<alpha), (q^{(t)}=q^*), 否则(q^{(t)}=q^{(t-1)}).
output: ({p^{(t)},q^{(t)}}).
注: 1中的标准正态分布不是唯一的, 但是文中选的便是这个. 4中的(p^*=-p)在实际编写程序的时候可以省去.
符号说明
因为作者从物理方程的角度给出几何解释,所以这里给出的符号一般有俩个含义:
| 符号 | 概率 | 物理 |
|---|---|---|
| (q) | 随机变量,服从我们所在意的分布 | 冰球的位置 |
| (p) | 用以构造马氏链的额外的变量 | 冰球的动量(mv) |
| (U(q)) | ...与我们所在意的分布有关 | 冰球的势能 |
| (K(p)) | ... | 冰球的动能 |
| (H(q, p)) | 与我们所在意的分布有关 | (H(q, p) = U(q) + K(p)) |
Hamilton方程
物理解释
Hamilton方程((i=1,2,ldots, d), (d)是维度):
这个东西怎么来的, 大概是因为(H(q, p) = U(q)+K(p)), 如果机械能守恒, 那么随着时间(t)的变化(H(q, p))应该是一个常数, 所以其关于t的导数应该是0.
其中(dot{p}=(partial{p_1}/partial t, ldots, partial p_d / partial t)).
而((2.1)), 左边是速度(dot{q} = v), 右边
不过,估计是先有的(2.2)再有的H吧, 就先这么理解吧. 需要一提的是, (K(p))通常定义为
其中(M)是对称正定的, 后面我们可以看到, 这种取法与正态分布相联系起来.
此时:
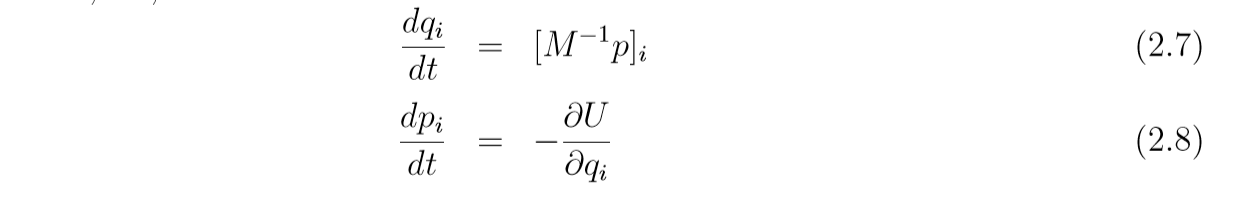
一些性质
可逆 Reversibility
映射(T_s: (q(t), p(t)) mapsto (q(t+s), p(t+s)))是一一的,这个我感觉只能从物理的解释上理解啊, 一个冰球从一个点到另一个点, 现在H确定, 初值确定, 不就相当于整个轨迹都确定了吗, 那从哪到哪自然是一一的, 也就存在逆(T_{-s}), 且只需:
H的不变性
即
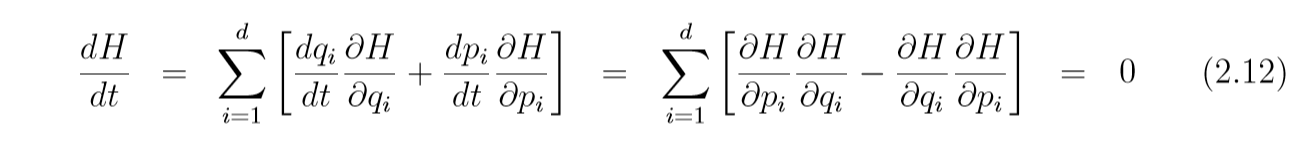
当然, 因为我们的算法是离散化的, 所以这个性质只是在(epsilon)比较小的时候近似保持.
保体积 Volume preservation
即假设区域(R={(q,p)})在映射(T_t)的作用下为(R_t={(q(t), p(t)}), 则二者的体积相同, 均为(V).
定义
其中(z = (q, p)). 又
其中
所以
又对于任意方阵(A),
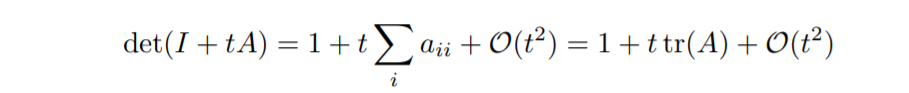
所以
且(mathrm{tr}(partial f / partial z)=mathrm{div} f), 于是
又
对于(t=t_0), 我们都可以类似的证明(dv(t_0)/dt=0), 所以(v(t))是常数.
这部分的证明参考自
辛 Symplecticness

离散化Hamilton方程 leapfrog方法
下面四幅图, 是(U(q)=q^2/2, K(p)=p^2/2), 起始点为((q, p) = (0, 1)).
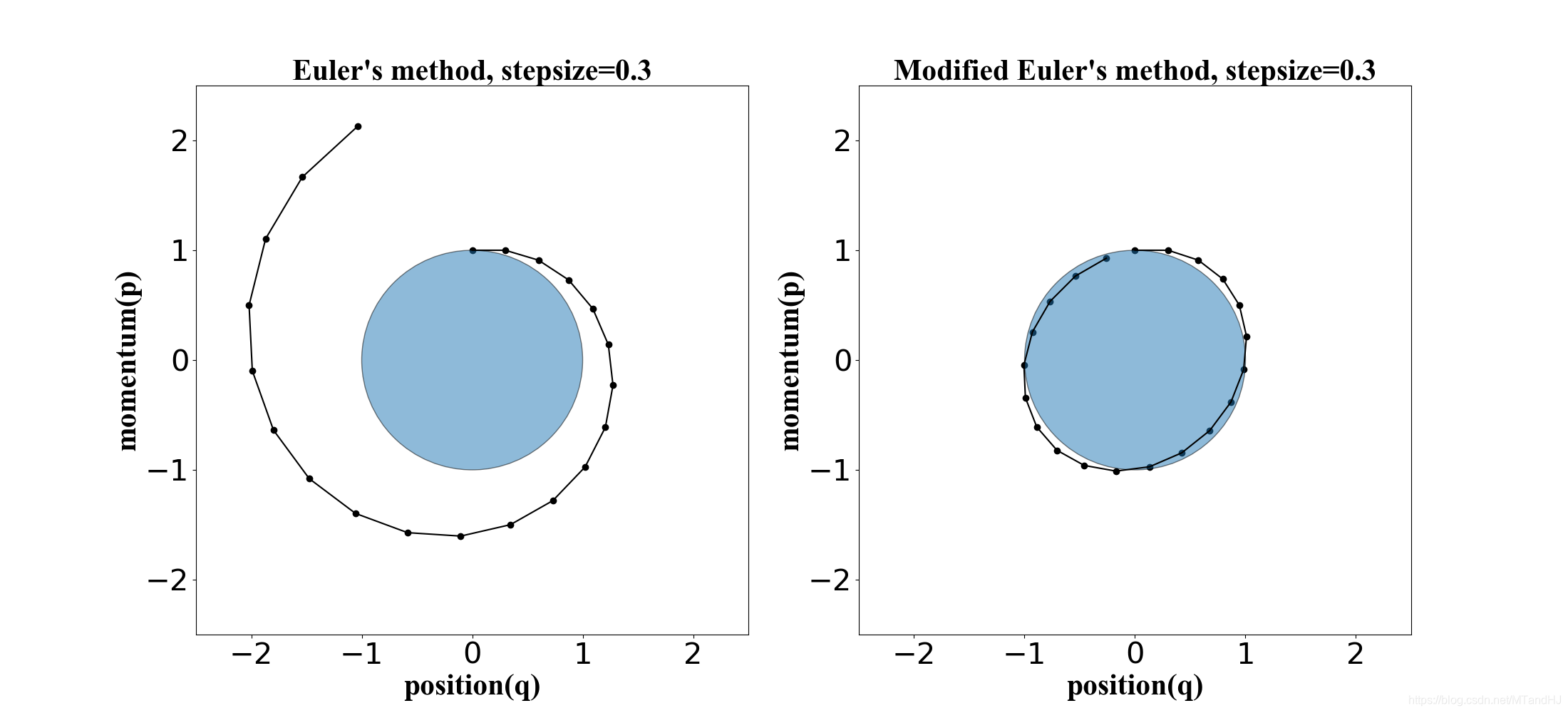
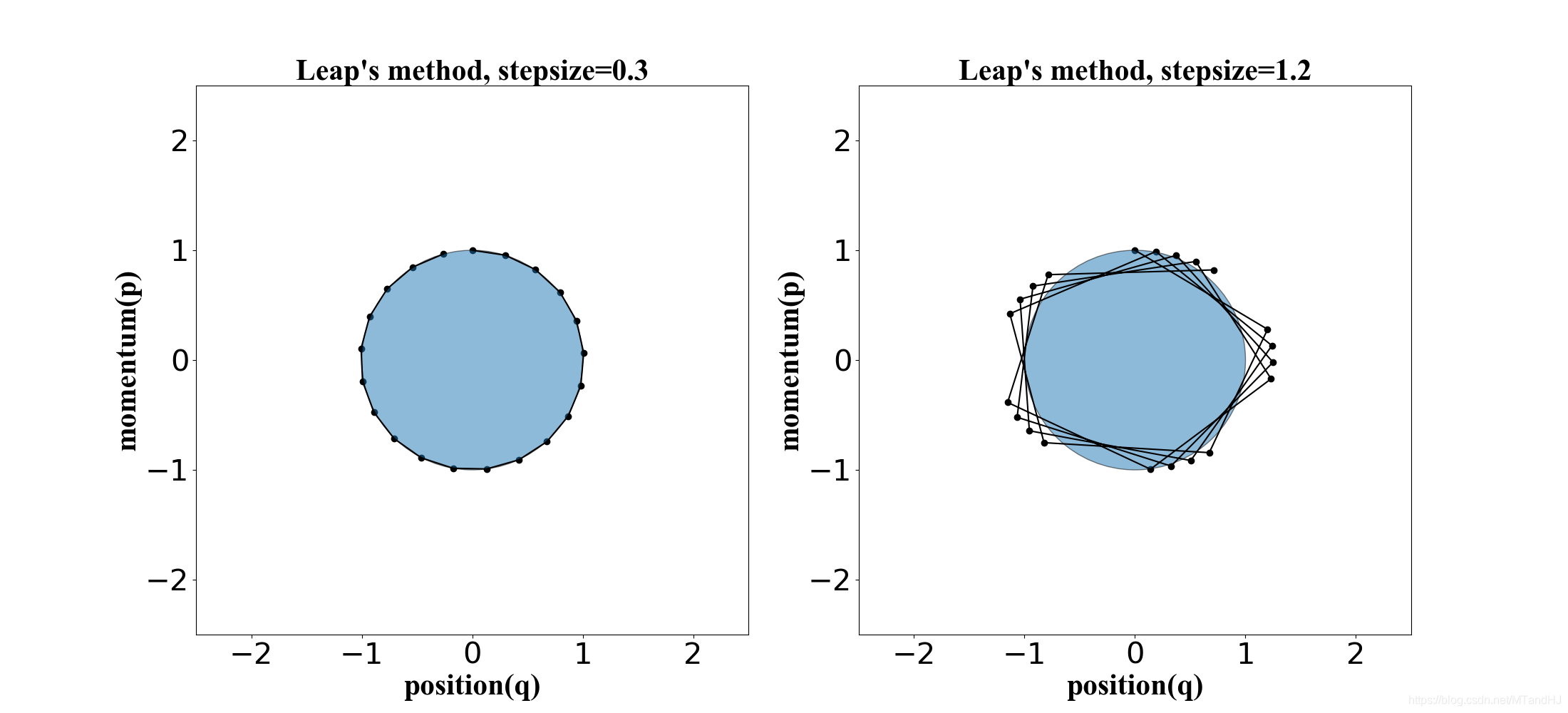
Euler's method
如果假定(K(p) = sum_{i=1}^d frac{p_i^2}{2m_i}),
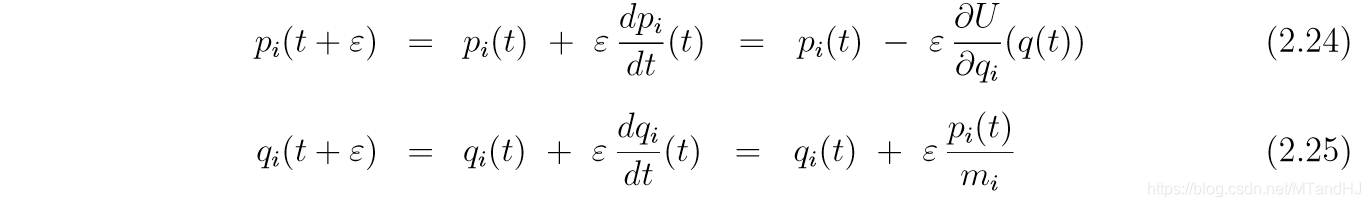
Modified Euler's method
仅有一个小小的变动,
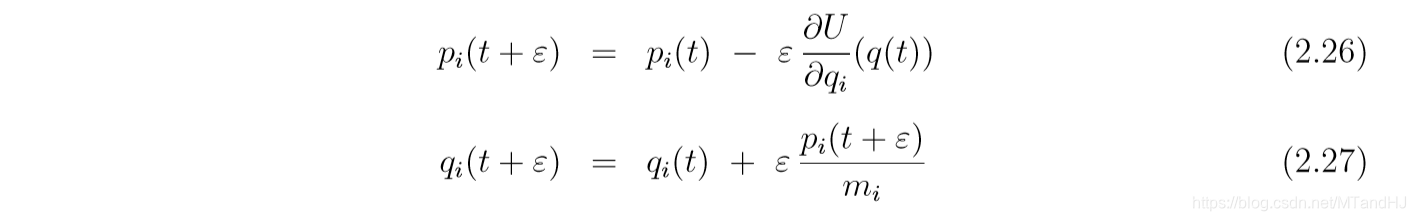
Leapfrog method
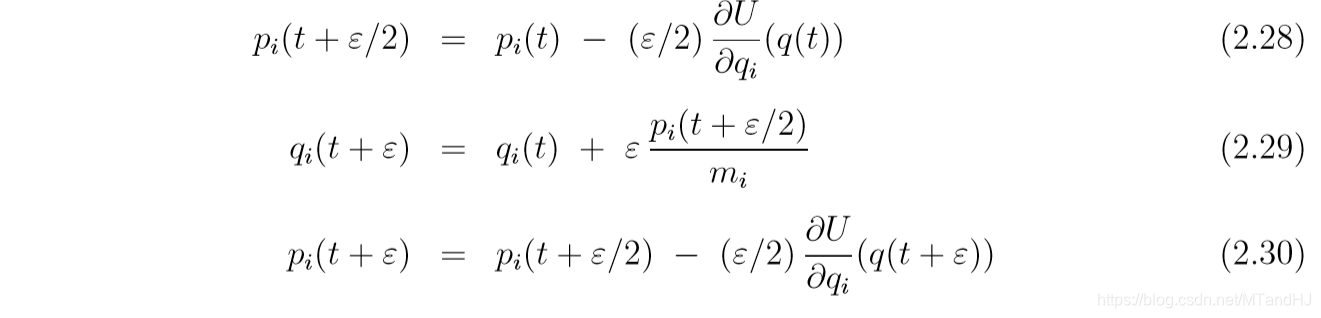
注意到, 在实际编写程序的时候, 除了第一步和最后一步, 我们可以将(p)的俩个半步合并成一步.
另外从右下角的图可以发现, 因为离散化的缘故, (H(q, p))的值是有偏差的. 但是Leapfrog 方法和 modified Euler方法都是保体积的, 因为每步更新都只改变一个量, 可以验证其雅可比行列式为1.
MCMC
概率与Hamiltonian, 正则(canonical)分布
如何将分布于Hamilton方程联系在一起? 假如, 我们关心的是(q)的分布(P(q)), 则我们构造一个容易采样的分布(P(q)),
其中(Z)是规范化的常数, (T)一般取1. 从(3.2)中容易得到(H(q,p)). 事实上此时(q, p)是独立的(这么写是说明直接构造(P(q, p))也是可以的), 则可以分别
在贝叶斯统计中, 有
其中(D)为数据, (L)为似然函数, 与文章中不同, 文章中是(L(q|D)), 应该是笔误.
HMC算法
就是开头提到的算法, 但是其中有一些地方值得思考. (alg.4)我们令(p^*=-p), 这一步在实际中是不起作用的, 既然(K(p)=K(-p))而且在下轮中我们重新采样(p), 我看网上的解释是为了理论, 取反这一部分使得proposal是对称的, 是建议分布(g(p^*, q^*|p, q)=g(p, q| p^*, q^*))? 不是很懂.
有点明白了, 首先因为Leapfrog是确定的, 所以(P(q^*, p^*|q, p))非0即1:
为了(P(q^*, p^*|q, p)=P(q, p|q^*, p^*)), 如果不取反肯定不行, 因为他就会往下走, 取反的操作实际上就是在可逆性里提到的, 在同样的操作下, (q^*, p^*)会回到(q, p). 于是MH接受概率就退化成了M接受概率. 但是前文也提到了, 取反的操作, 只有在(K(p)=K(-p))的情况下是成立的.
HMC保持正则分布不变的证明 detailed balance
假设({A_k})是((q, p) in mathbb{R}^{2d})空间的一个分割, 其在L次leapfrog的作用, 及取反的操作下的像为({B_k}), 由于可逆性, ({B_k})也是一个分割, 且有相同的体积(V)(保体积性),则
实际上(i
ot =j)是时候是显然的, 因为二者都是0. 因为(H)是连续函数, 当(V)变得很小的时候, (H)在(X)区域上的值相当于常数(H_X), 于是
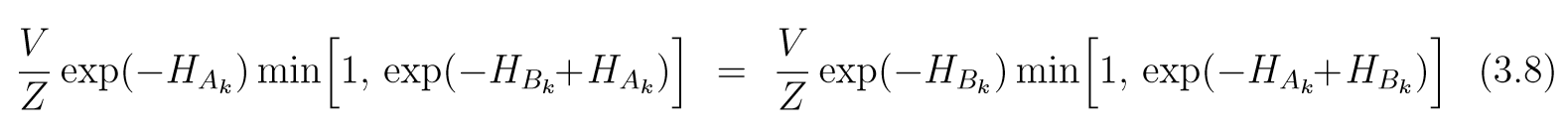
所以(3.7)成立.
Detailed balance:
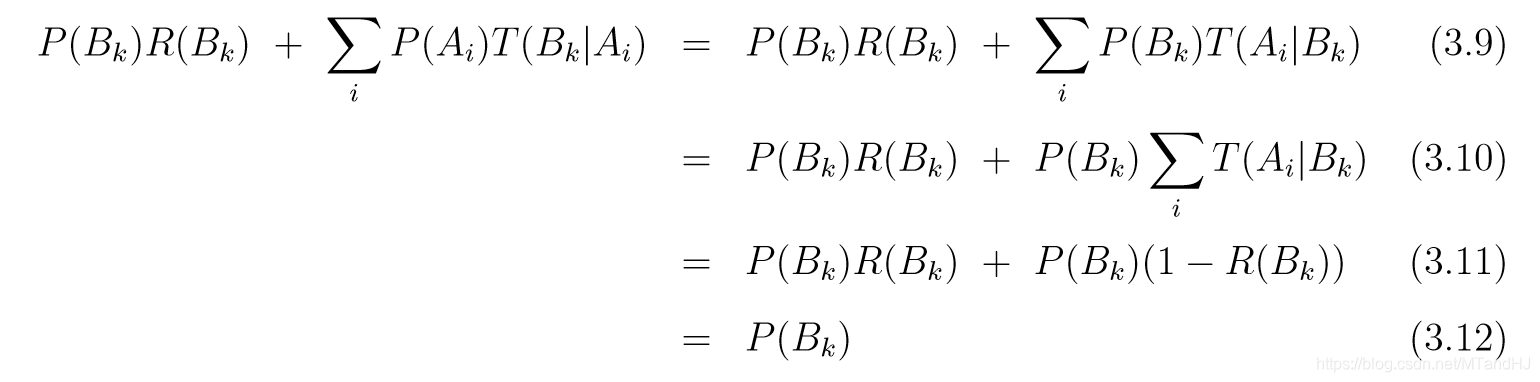
其中(R(X))是当前状态属于(X), 拒绝提议的((q^*,p^*))的概率. 注意(sum_{i} T(A_i|B_k)=T(A_k|B_k)=1-R(B_k)). 看上面的连等式可能会有点晕, 注意到, 左端实际上是概率(P{q^{(t)}, p^{(t)}) in B_k}), 最右端是(P{(q^{(t-1)}, p^{(t-1)}) in B_k}), 这样就能明白啥意思了.
遍历性 Ergodicty
马氏链具有遍历性才会收敛到一个唯一的分布上(这部分不了解), HMC是具有这个性质的, 只要(L)和(epsilon)选的足够好. 但是如果选的不过也会导致坏的结果, 比如上面的图, (p^2+q^2=1), 如果我们选择了(Lepsilon approx 2pi), 那么我们的Leapfrog总会带我们回到原点附近, 这就会导致比较差的结果.
HMC的一个例子及优势
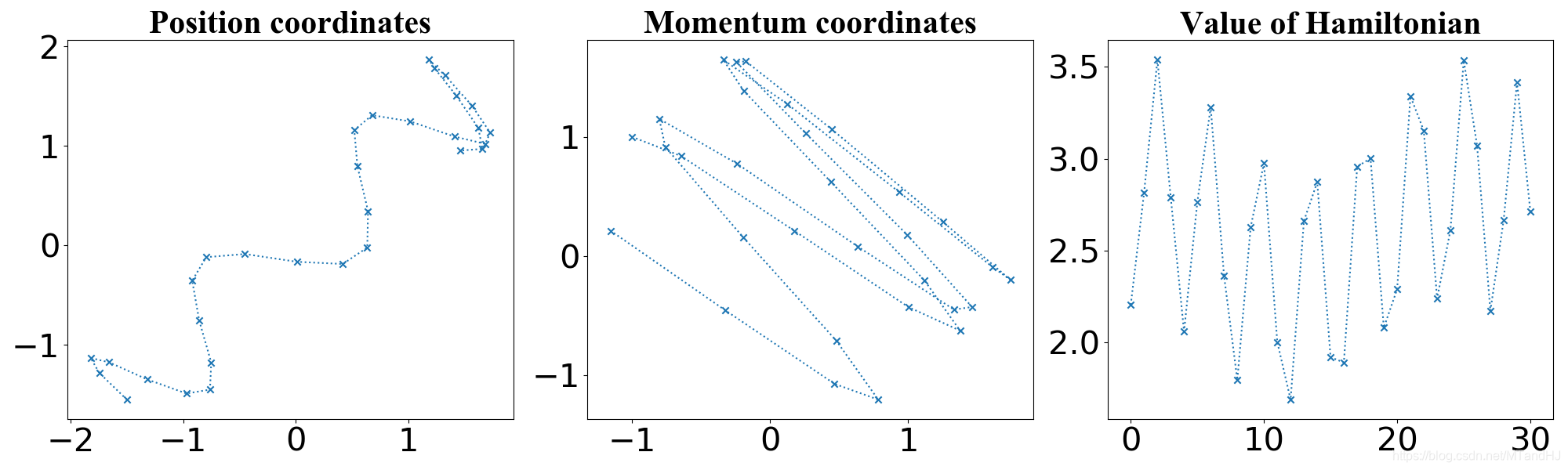
下图是:
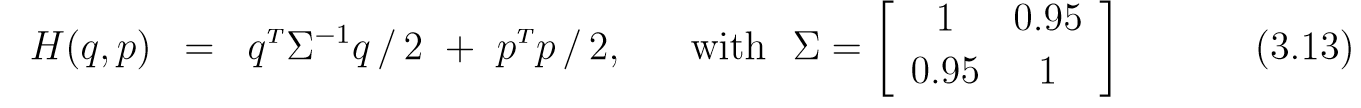
(epsilon=0.25, L=30, q = [-1.5, -1.55]^T, p=[-1, 1^T]).
相关系数由(0.95)改为(0.98), (epsilon=0.18, L=20), 随机游走取的协方差矩阵为对角阵, 标准差为(0.18), HMC生成(p)的为标准正态分布.
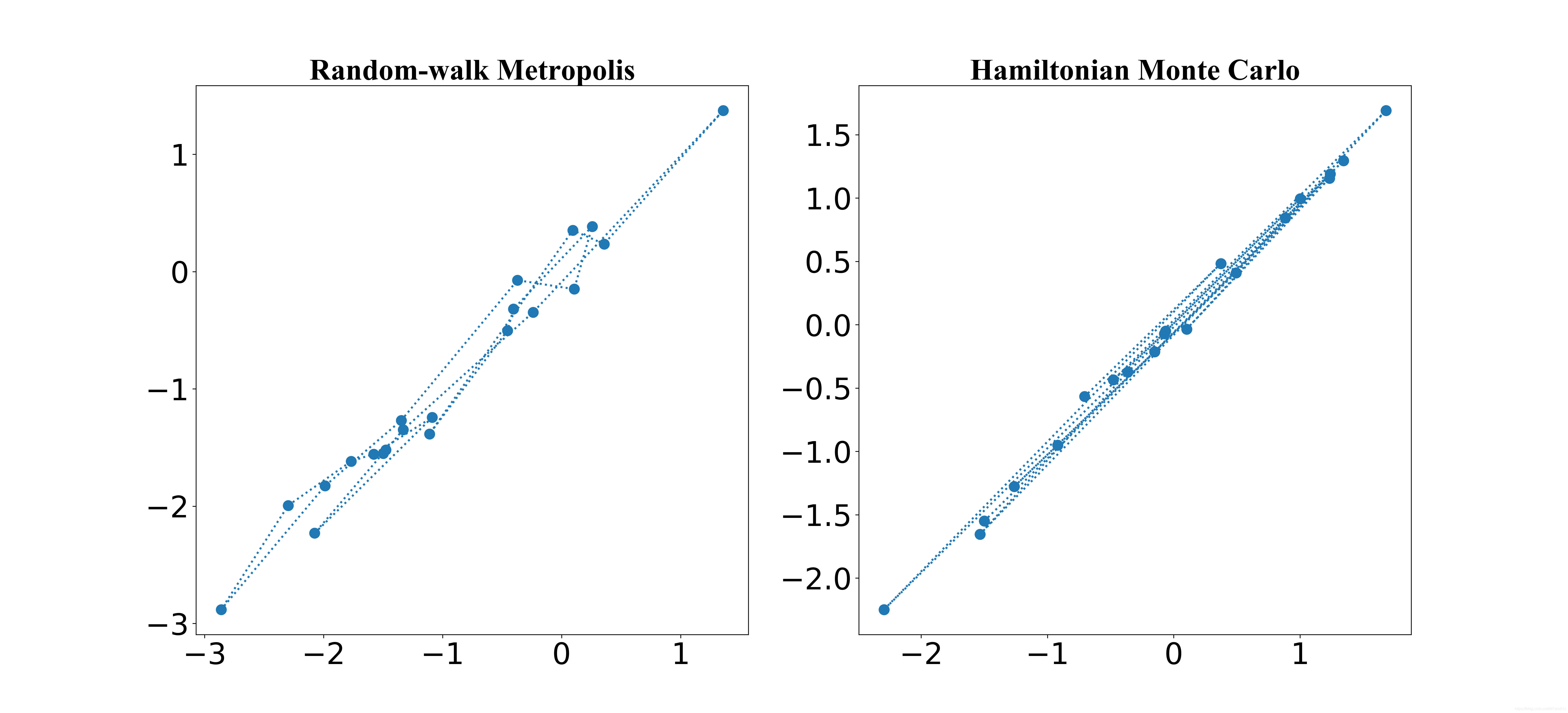
文章中提到, HMC较Randomwalk的优势在于,Randomwalk对协方差很敏感, 而且太大会导致接受率很低, 太小俩俩之间的相关性又会太高.
HMC在实际中的应用和理论
线性变换
有些时候, 我们会对变量施加线性映射(q'=Aq)((A)非奇异方阵), 此时新的密度函数(P'(q') = P(A^{-1}q') / |det (A)|), 其中(P(q))是(q)的密度函数, 相应的我们需要令(U'(q')=U(A^{-1}q')).
如果我们希望线性变化前后不会是的情况变得"更糟", 一个选择是(p'=(A^T)^{-1}p),则(K'(p')=K(A^Tp')), 如果(K(p) = p^TM^{-1}p / 2), 则
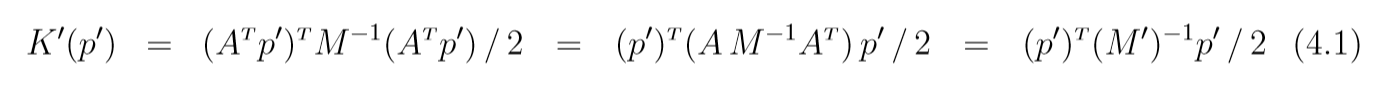
其中(M' = (AM^{-1}A^T)^{-1}=(A^{-1})^TMA^{-1}). 此时((q', p'))的更新会使得原先的((q,p))的更新保持, 即
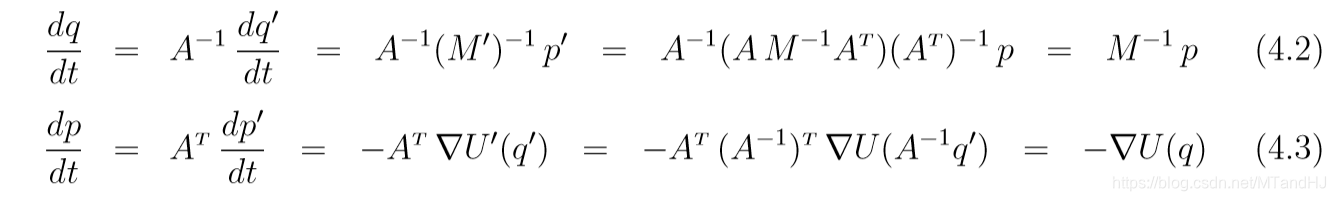
所以((q, p))本质上按照原来的轨迹发生着变化.
设想, 我们对(q)的协方差矩阵有一个估计(Sigma), 且近似服从高斯分布, 我们可以对其做Cholesky分解(Sigma=LL^T), 并且令(q'=L^{-1} q), 则(q')的各分量之间就相互独立了, 那么我们很自然的一个选择是(K(p)=p^Tp/2), 那么(q')的各分量的独立性能够保持.
另一个做法是, 保持(q)不变, 但是(K(p) = p^T Sigma p / 2), 此时(q'=L^{-1}q, p'=(L^{T})^{-1}p), 则相当于
所以俩个方法是等价的.
HMC的调整(epsilon, L)
HMC对(epsilon, L)的选择比较严苛.
预先的实验
我们可以对一些(epsilon,L)进行实验, 观察轨迹, 虽然这个做法可能产生误导, 另外在抽样过程中随机选择(epsilon, L)是一个不错的选择.
stepsize (epsilon)
(epsilon)的选择很关键, 如果太大, 会导致低的接受率, 如果太小, 不仅会造成大量的计算成本, 且如果此时(L)也很小, 那么HMC会缺乏足够的探索.
考虑下面的例子:
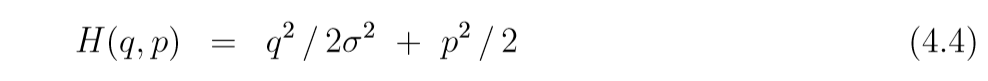
每一次leapfrog将((q(t), p(t)))映射为((q(t+s), p(t+s))), 则
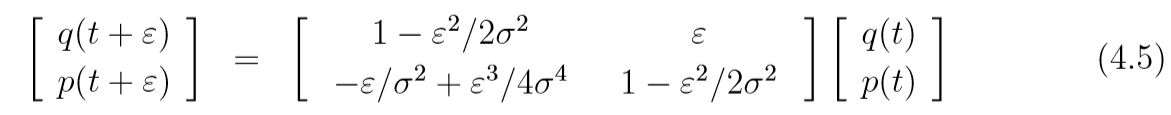
((q, p))是否稳定, 关键在于系数矩阵的特征值的模(?还是实部)是否小于1, 特征值为
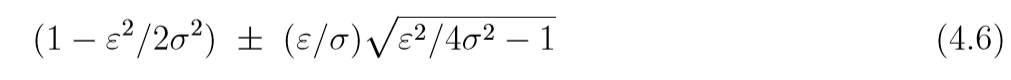
当(epsilon>2sigma)的时候,(4.6)有一个实的大于1的特征值, 当(epsilon < 2 sigma)的时候, 特征值是复制, 且模为:
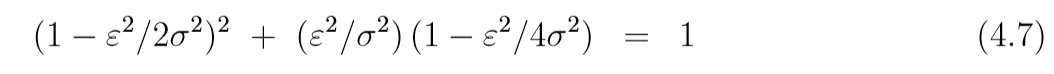
所以, 我们应当选择(epsilon < 2sigma).
在多维问题中, (K(p)=p^Tp/2),如果(q<0)且协方差矩阵为(Sigma), 我们可以取协方差矩阵的最小特征值(非零?)作为步长. 如果(K(p)=p^TM^{-1}p/2), 我们可以通过线性变化将其转换再考虑.
tracjectory length (L)
如何选择(L)也是一个问题, 我们需要足够大的(L)使得每次的探索的足够的, 以便能够模拟出独立的样本, 但是正如前面所讲, 大的(L)不仅会带来计算成本, 而且可能会导致最后结果在起点附近(由周期性带来的麻烦). 而且(L)没法通过轨迹图正确的选择. 一个不错的想法是在一个小的区间内随机选择(L), 这样做可能会减少由于周期性带来的麻烦.
多尺度
我们可以利用(q)的缩放信息, 为不同的(q_i)添加给予不同的(epsilon_i). 比方说在(K(p)=p^Tp/2)的前提下, 应该对(q_i)放大(s_i)倍, 即(q'= q / s_i)((p)不变).
等价的, 可以令(K(p) = p^TM^{-1}p / 2, m_i = 1/ s_i^2)((q)不变), 相当于(q_i'=q_i/s_i, p'=s_ip), 则
(m_i' = s_i (1/ s_i^2)s_i=1), 所以(K(p')=(p')^Tp'/2). 这么做就相当于一次leapfrog为:
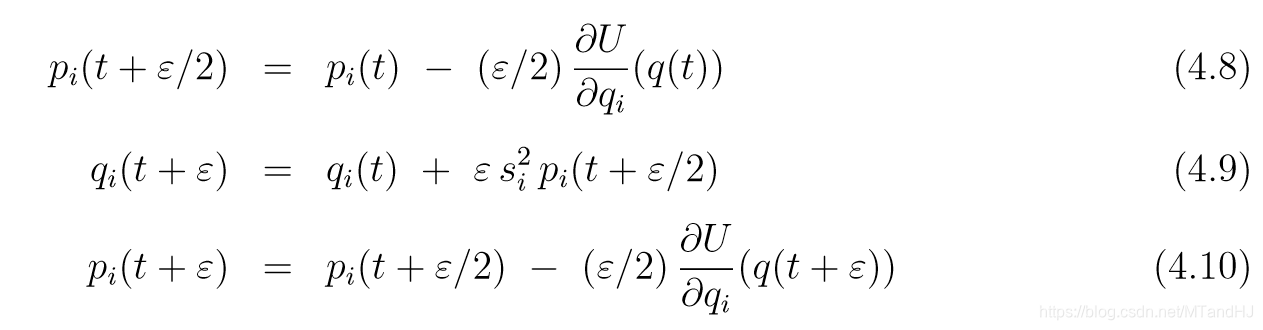
结合HMC与其它MCMC
当我们所关心的变量是离散的, 或者其对数概率密度((U(q)))的导数难以计算的时候, 结合其它MCMC是有必要的.
Scaling with dimensionality
(U(q) = sum u_i(q_i))的情况
如果(U(q)=sum u_i(q_i)), 且(u_i)之间相互独立(?), 这种假设是可行的, 因为之前已经讨论过, 对于(q)其协方差矩阵为(Sigma), 我们可以通过线性变化使其对角化, 且效能保持.
Cruetz指出, 任何的Metropolis形式的算法在采样密度函数(P(x)=frac{1}{Z}exp(-E(x)))的时候都满足:
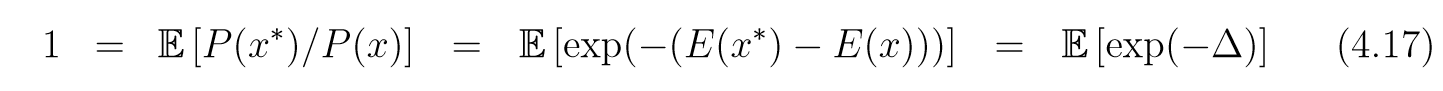
其中(x)表现在的状态, 而(x^*)表提议. 则根据Jensen不等式可知:
所以(mathbb{E}[-Delta]le 0),
在(U(q) = sum u_i(q_i))的情况下, 令(Delta_1:=E(x^*)-E(x)), (x=q_i, E(x)=u_i(q_i))或者(x=(q_i, p_i), E(x)=u_i(q_i)=p_i^2/2). 对于整个状态, 我们则用(Delta_d)表示, 则(Delta_d)是所有(Delta_1)的和. 既然(Delta)的平均值均为正, 这会导致接受概率(min (1, exp(-Delta_d))的减小(随着维度的增加), 除非以减小步长作为代价, 或者建议分布的宽度进一步降低(即(x,x^*)尽可能在一个区域内).
因为(exp(-Delta_1) approx 1 -Delta_1+Delta_1^2 / 2), 再根据(4.17)得:
故(Delta_1)的方差约是均值的两倍((Delta_1)足够小的时候), 类似的也作用与(Delta_d). 为了有一个比较好的接受率, 我们应当控制(Delta_d)的均值在1左右(小于?), 此时(exp(-1)approx0.3679).
HMC的全局误差(标准差)在(mathcal{O}(epsilon^2))级别, 所以(Delta_1^2)应当在(epsilon^4)级别, 所以(mathbb{E}[Delta_1])也应当在(epsilon^4)级别, 则(mathbb{E}[Delta_d])在(depsilon^4)级别上, 所以为了保持均值为1左右, 我们需要令(epsilon)正比于(d^{-1/4}), 相应的(L)为(d^{1/4}).
文章中还有关于Randomwalk的分析, 这里不多赘述了.
HMC的扩展和变种
这个不一一讲了, 提一下
分割
假如(H)能够分解成:

那么我们可以一个一个来处理, 相当于(T_{1, epsilon} circ T_{2, epsilon}, circ cdots circ T_{k-1, epsilon} circ T_{k, epsilon}). 这个做法依旧是保体积的(既然每一个算子都是保体积的), 但是如果希望其可逆(对称), 这就要求(H_i(q, p)=H_{k-i+1}(q, p).) 这个有很多应用场景:
比如(U(q) = U_0(q)+U_1(q)), 其中计算(U_0)如果是容易的, 我们可以作如下分解:
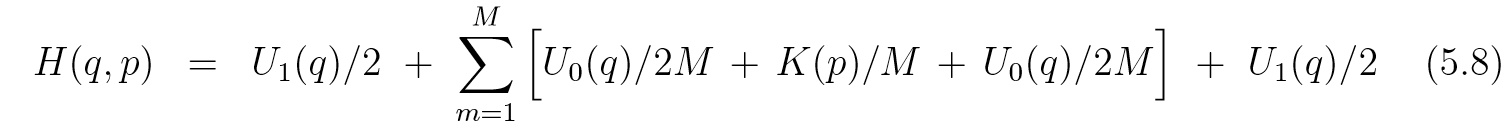
此时有(3M+2)项, (H_1(q, p) = H_k(q, p)=U_1(q)/2), (H_{3i-1}=H_{3i+1}=U_0(q)/2M), (H_{3i}=K(p)/M). 此时对于中间部分, 相当于步长变小了,误差自然会小.
当处理大量数据, 并用到似然函数的时候:

不过文章中说这个分解是不对称的, 可明明是对称的啊.
处理约束
有些时候, 我们对(q)有约束条件, 比方(q >v, q<w)等等, 直接给算法:

Langevin method, LMC
假设我们使用(K(p)=(1/2)sum p_i^2), (p)从标准正态分布中采样, 每次我们只进行一次leapfrog变计算接受概率, 即
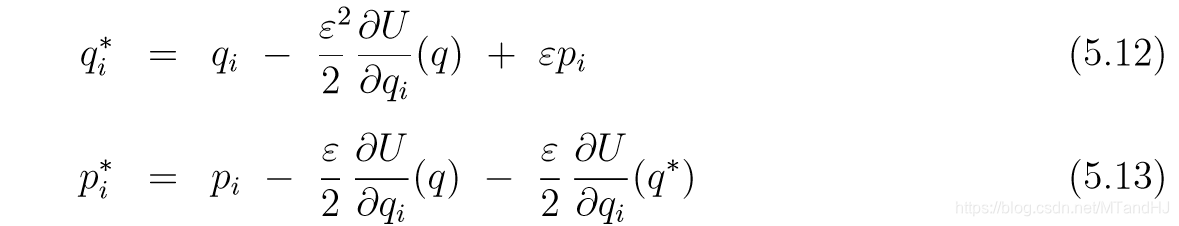
以及其接受概率:
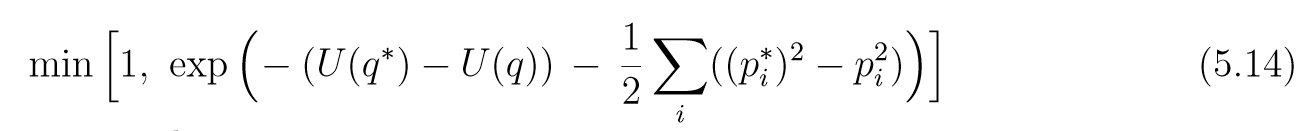
Windows of states
这个方法试图将(H)的曲线平滑来提高接受率.
我们可以通过任意((q, p))构造一列([(q_0, p_0), ldots, (q_{W-1}, p_{W-1})]). 首先从({0, 1, ldots, W-1})中等概率选一个数, 这个数代表((q, p))在序列中的位置, 记为((q_s, p_s)), 则其前面的可以通过leapfrog ((-epsilon))产生, 后面的通过leapfrog((+epsilon))产生. 所以任意列的概率密度为:
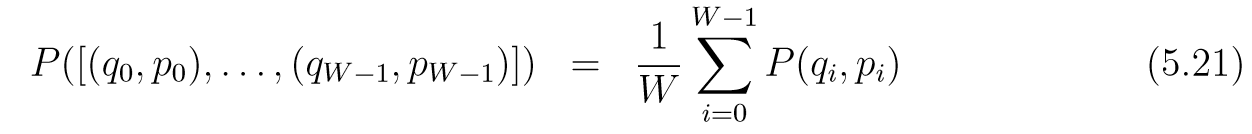
然后从((q_{W-1}, p_{W-1}))出发, 通过L-W+1步leapfrog((+epsilon))获得([q_W,p_W,ldots, (q_L, p_L)])并定义提议序列为([(q_L, -p_{L}), ldots, (q_{L-W+1}, p_{L-W+1)}]),计算接受概率:
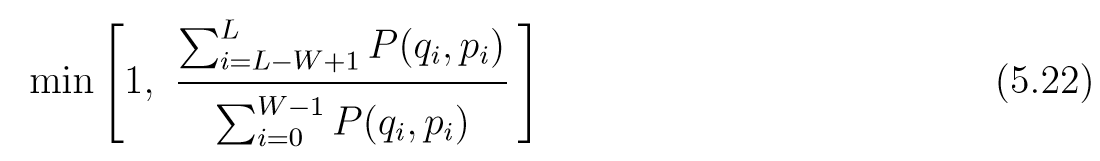
其中(P(q, p)propto exp(-H(q,p))). 设拒绝或者接受后的状态为:([(q_0^+, p_0^+), ldots, (q_{W-1}^+, p_{W-1}^+)]), 依照概率

抽取((q_e^+, p_e^+)), 这个就是((q,p))后的下一个状态.
文中说这么做分布不变, 因为:
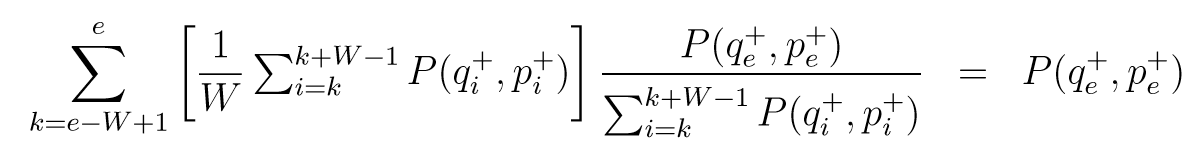
如果没理解错, 前面的部分就是((q_e^+, p_e^+))出现在最开始的序列中的概率, 但是中间的接受概率哪里去了? 总不能百分百接受吧...
代码
import numpy as np
from collections.abc import Iterator, Callable
from scipy import stats
class Euler:
"""
Euler方法
"""
def __init__(self, grad_u, grad_k, epsilon):
self.grad_u = grad_u
self.grad_k = grad_k
self.epsilon = epsilon
def start(self, p, q, steps):
trajectory_p = [p]
trajectory_q = [q]
for t in range(steps):
temp = p - self.epsilon * self.grad_u(q) # 更新一步P
q = q + self.epsilon * self.grad_k(p) # 更新一步q
p = temp
trajectory_p.append(p)
trajectory_q.append(q)
return trajectory_p, trajectory_q
def modified_start(self, p, q, steps):
"""
启动!
:param p:
:param q:
:param steps: 步数
:return: p, q
"""
trajectory_p = [p]
trajectory_q = [q]
for t in range(steps):
p = p - self.epsilon * self.grad_u(q) #更新一步P
q = q + self.epsilon * self.grad_k(p) #更新一步q
trajectory_p.append(p)
trajectory_q.append(q)
return trajectory_p, trajectory_q
class Leapfrog:
"""
Leapfrog 方法
"""
def __init__(self, grad_u, grad_k, epsilon):
self.grad_u = grad_u
self.grad_k = grad_k
self.epsilon = epsilon
self.trajectory_q = []
self.trajectory_p = []
def start(self, p, q, steps):
self.trajectory_p.append(p)
self.trajectory_q.append(q)
for t in range(steps):
p = p - self.epsilon * self.grad_u(q) / 2
q = q + self.epsilon * self.grad_k(p)
p = p - self.epsilon * self.grad_u(q) / 2
self.trajectory_q.append(q)
self.trajectory_p.append(p)
return p, q
class HMC:
"""
HMC方法
start为进行一次
accept_prob: 计算接受概率
hmc: 完整的过程
acc_rate: 接受概率
"""
def __init__(self, grad_u, grad_k, hamiltonian, epsilon):
assert isinstance(grad_u, Callable), "function needed..."
assert isinstance(grad_k, Callable), "function needed..."
assert isinstance(hamiltonian, Callable), "function needed..."
self.grad_u = grad_u
self.grad_k = grad_k
self.hamiltonian = hamiltonian
self.epsilon = epsilon
self.trajectory_q = []
self.trajectory_p = []
def start(self, p, q, steps):
self.trajectory_p.append(p)
self.trajectory_q.append(q)
p = p - self.epsilon * self.grad_u(q) / 2
for t in range(steps-1):
q = q + self.epsilon * self.grad_k(p)
p = p - self.epsilon * self.grad_u(q)
q = q + self.epsilon * self.grad_k(p)
p = p - self.epsilon * self.grad_u(q) / 2
p = -p
return p, q
def accept_prob(self, p1, q1, p2, q2):
"""
:param p1: 原先的
:param q1:
:param p2: 建议的
:param q2:
:return:
"""
p1 = np.exp(self.hamiltonian(p1, q1))
p2 = np.exp(self.hamiltonian(p2, q2))
alpha = min(1, p1 / p2)
return alpha
def hmc(self, generate_p, q, iterations, steps):
assert isinstance(generate_p, Iterator), "Invalid generate_p"
self.trajectory_q = [q]
p = next(generate_p)
self.trajectory_p = [p]
count = 0.
for t in range(iterations):
tempp, tempq = self.start(p, q, steps)
if np.random.rand() < self.accept_prob(p, q, tempp, tempq):
p = tempp
q = tempq
self.trajectory_p.append(p)
self.trajectory_q.append(q)
count += 1
p = next(generate_p)
self.acc_rate = count / iterations
return self.trajectory
@property
def trajectory(self):
return np.array(self.trajectory_p),
np.array(self.trajectory_q)
class Randomwalk:
"""
walk: 完整的过程, 实际上Metropolis更新似乎就是start中steps=1,
一开始将文章的意思理解错了, 不过将错就错, 这样子也能增加一下灵活性.
"""
def __init__(self, pdf, sigma):
assert isinstance(pdf, Callable), "function needed..."
self.pdf = pdf
self.sigma = sigma
self.trajectory = []
def start(self, q, steps=1):
for t in range(steps):
q = stats.multivariate_normal.rvs(mean=q,
cov=self.sigma)
return q
def accept_prob(self, q1, q2):
"""
:param q1: 原始
:param q2: 建议
:return:
"""
p1 = self.pdf(q1)
p2 = self.pdf(q2)
alpha = min(1, p2 / p1)
return alpha
def walk(self, q, iterations, steps=1):
self.trajectory = [q]
count = 0.
for t in range(iterations):
temp = self.start(q, steps)
if np.random.rand() < self.accept_prob(q, temp):
q = temp
count += 1
self.trajectory.append(q)
self.acc_rate = count / iterations
return np.array(self.trajectory)