A Deep Neural Network’s Loss Surface Contains Every Low-dimensional Pattern

目录

• 概
• 相关工作
• 主要内容
  • 引理1
  • 定理1
  • 定理2

A Deep Neural Network’s Loss Surface Contains Every Low-dimensional Pattern

概

作者关于Loss Surface的情况做了一个理论分析, 即证明足够大的神经网络能够逼近所有的低维损失patterns.

相关工作

loss landscape 的提及.

文中多处用到了universal approximators.

主要内容

引理1

(mathcal{F})定义了universal approximators, 即同一定义域内的任意函数(f)都能用(mathcal{F})中的元素来逼近. (sigma(f_ heta))则是将值域进行了扩展, 而这并不影响其universal approximator的性质.

定理1

证明:

假设神经网络的第一层的权重矩阵为( heta_W in mathbb{R}^{d imes k}), 偏置向量为( heta_b), 神经网络剩余的参数为( heta'), 记( heta = { heta_W, heta_b, heta'}). 则网络的输出为:

[ ag{1} f_{ heta}(x) = f_{{ heta_W, heta_b, heta' }}(x) = g_{ heta'}(langle x, heta_W angle + heta_b), ]

(N)个样本点的损失就是

[ ag{2} L( heta) = frac{1}{N} sum_i ell (f_{ heta}(x_i), y_i). ]

现在假设目标(z)维loss pattern为(应当为连续函数)

[ ag{3} mathcal{T}(h_1,h_2,ldots, h_z):[0,1]^z ightarrow [0, 1]. ]

我们现在, 希望将网络中的某些参数视作变量(h_1,ldots,h_z), 得以逼近(mathcal{T}).

令( heta_W=0) (这样网络的输出与(x)无关), ( heta_b=[h_1,ldots, h_z,0,ldots,0])(这隐含了(k ge z)的假设).

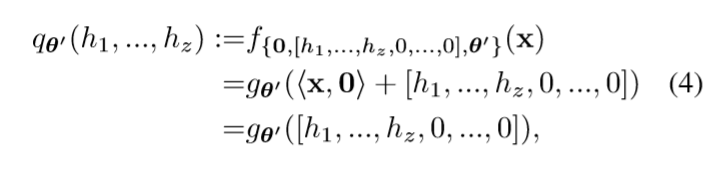
根据universal approximation theorem我们可以使得(q_{ heta'})成为approximator. 相对应的

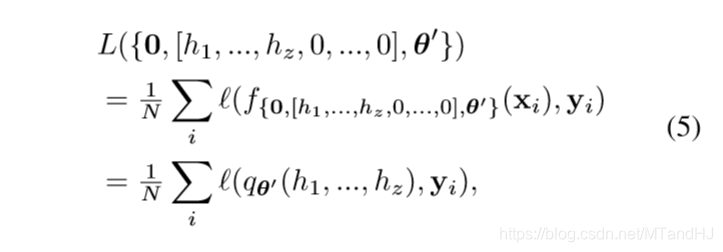
定义(sigma(p):=frac{1}{N}sum_i ell(q_{ heta'}(h_1,ldots, h_z),y_i)), 只需要(sigma)满足引理1中的条件, 就存在( heta_{epsilon}(mathcal{T})), 使得(L(h_1,h_2,ldots, h_z, heta_{epsilon}(mathcal{T})))逼近(mathcal{T}).

定理2

说实话, 这个定理没怎么看懂, 看证明, 这个global minimum似乎指的是(mathcal{T}(h))的最小值.

证明:

( heta_b)不变, ( heta_W)只令前(z)列为0, 则第一层(未经激活)的输出为((h_1,ldots,h_z，phi(x))), 于是

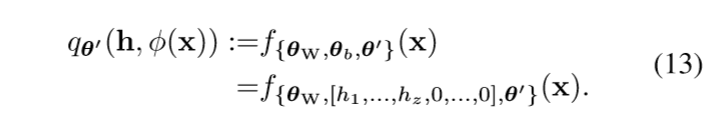
令(h^* := arg min_{h in [0,1]^z mathcal{T}(h)}), 并假设(L^*=mathcal{T}(h^*))(?). 假设损失(ell_i(p) = ell (p, y_i)), 可逆且逆函数光滑(这个性质对于损失函数来讲很普遍).

在这个假设下, 我们有

[ ag{14} q_{ heta'}(h, phi(x_i)) approx ell_i^{-1}(mathcal{T}(h)), ]

文中说这个也是因为逼近定理, 固定(i)的时候, 这个自然是成立的, 如何能保证对于所有的(i=1,ldots,n)成立, 我有一个思路.

假设二者的距离((+infty)范数)为(epsilon_i^h in mathbb{R}), 则

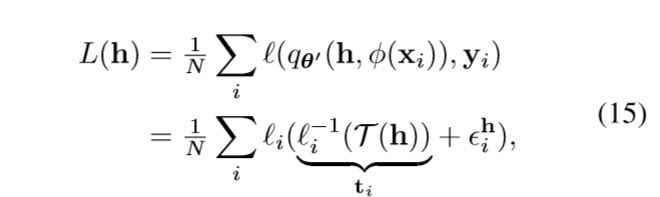
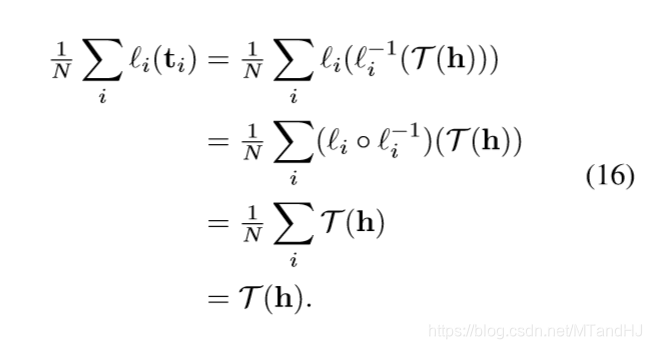
所以

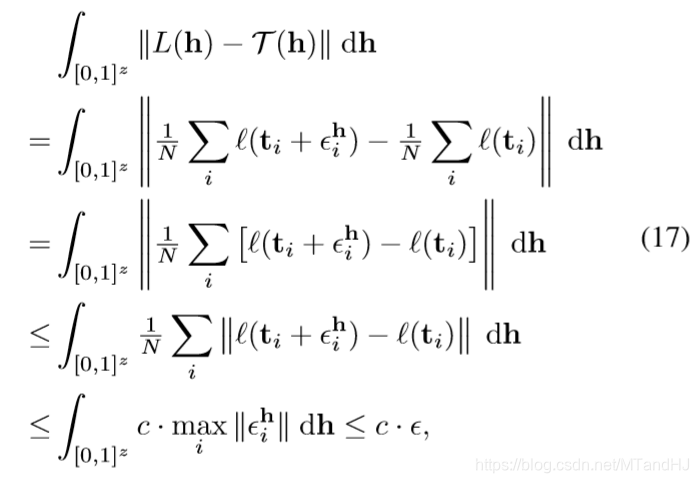
且此时(|L(h^*)-mathcal{T}(h^*)|<epsilon).

我比较关心的问题是, 能否选择合适的loss patterns (相当于选择合适的空间) 使得网络在某些性能上比较好(比方防过拟合, 最优性).