Entropy Search for Information-Efficient Global Optimization

目录

• 概
• 主要内容
  • $p_{min}$的估计
  • $mathcal{L}_{KL}$的估计
  • $langle Delta mathcal{L} angle$

Hennig P, Schuler C J. Entropy search for information-efficient global optimization[J]. Journal of Machine Learning Research, 2012, 13(1): 1809-1837.

@article{hennig2012entropy,
title={Entropy search for information-efficient global optimization},
author={Hennig, Philipp and Schuler, Christian J},
journal={Journal of Machine Learning Research},
volume={13},
number={1},
pages={1809--1837},
year={2012}}

概

贝叶斯优化中的 Entropy Search (EI) 方法.

主要内容

这篇文章关注的是

[max_{x in I} :f(x), ]

的问题, 且假设定义域(I)是有界的.

一般, 通过高斯过程定义(f(x))的概率替代函数, 假设

[f(x) sim mathcal{N}(u_0(x), k(x,x)),\ y = f(x) + epsilon, : epsilon sim mathcal{N}(0, sigma^2). ]

在已经观测到(X = {x_1, ldots, x_T})以及(Y = {y_1, ldots, y_T})的基础上, 我们可以求得(f(x^*))的后验分布为以

[mu (x^*) = mu_0(x^*) + k(x^*, X)^T [k(X, X) + sigma I]^{-1}(Y-u_0(X)) \ sigma_*^2(x^*)=k(x^*, x^*) - k(x^*, X)^T (k(X,X)+sigma I)^{-1}k(x^*,X) ]

为均值和方差的正态分布.

我们的目的是在已有这些条件的基础上, 寻找下一个(或多个)评估点.

定义:

[ ag{1} p_{min}(x) =p[x = arg min f(x)] = int_{ f:I ightarrow R} p(f) prod_{ ilde{x} in I, ilde{x} ot = x} heta[f( ilde{x})-f(x)] mathrm{d}f, ]

其中( heta(x) = 1, xge0, else : 0). (prod)的部分在针对连续型的定义域时需要特别的定义. 显然(1)表示(x)为最小值点的概率.

再定义损失函数(当然损失函数不选择KL散度也是可以的, 但这是EI的名字的由来):

[ ag{2} mathcal{L}(p_{min}) = mathcal{L}_{KL}(p_{min})=-int_Ip_{min}(x) log frac{p_{min}(x)}{b(x)} mathrm{d}x. ]

当我们选择(b(x))为(I)上的均匀分布的时候, 当我们最小化(mathcal{L})的时候, (p_{min})会趋向Dirac分布(即某个点处的概率密度为无穷, 其余为0, 显然, 该点我们有足够的信心认为其是(f(x))的最小值点).

但是这样还不够, 我们进一步关心其期望损失(最小化):

[ ag{3} langle mathcal{L} angle_{x} = int p(y|x) mathcal{L}(p_{min} (cdot|Y, X, y, x)) mathrm{d}y. ]

通过最小化(3)，我们可以获得接下来的评估点.

接下来的问题是如果去估计.

(p_{min})的估计

比较麻烦的是(prod)的部分, 策略是挑选(N)个点( ilde{x} = { ilde{x}_1, ldots, ilde{x}_N}). 一种是简单粗暴的网格的方式, 但是这种方式往往需要较大的(N), 另一种是给定一个测度(u), 根据已有的观察((X, Y)), 通过(u(X, Y))采样( ilde{x}). 一个好的(u)应该在使得令损失能够产生较大变化的区域多采样点, 针对本文的情况 应该在(p_{min})值比较高的地方多采样点.

文中给了俩种方法, 一种直接的方法是(p_{min})可以用蒙特卡洛积分去逼近,

一下是我猜想的用MC积分的方式(文中未给出具体的形式)"

• 根据一定策略选取( ilde{x});
• 重复J次:

1. 根据概率(p(f))采样(f( ilde{x}), f(x)),
2. 计算(prod)部分

• 取平均

作者选择的是 Expectation Propagation (EP）的方法, 这种方法能够估计出( ilde{x}_i, i=1,ldots,N)处的概率(q_{min}( ilde{x_i})): (f_{min})存在于以( ilde{x}_i)为"中心"的一定范围内(文中用step)的概率. 当(N)足够的的时候, 这个step正比于((Nu( ilde{x}_i))^{-1}), 则:

[p_{min}(x) approx frac{q_{min}(x_i)Nu( ilde{x}_i)}{Z_u}, : Z_u=int u(x) mathrm{d}x, : x_i = arg min_{x_i in ilde{x}} |x-x_i|. ]

这样我们就完成了(p_{min})的估计, 一个更加好的性质是(q_{min})关于(mu, sigma_*)的导数是有解析表达式的, 且(Z_u)是不必计算的(后续最小化过程中可以省略掉).

(mathcal{L}_{KL})的估计

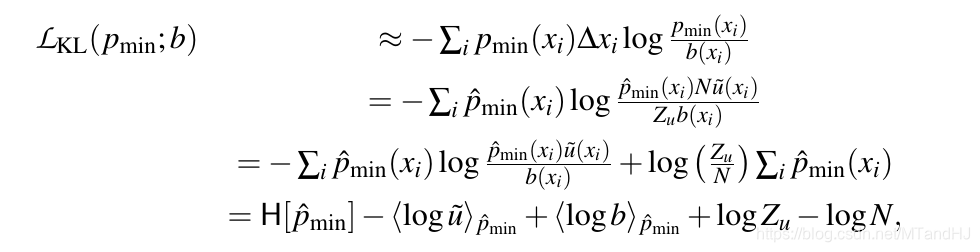
其中(hat{p}_{min}=q_{min}).

(langle Delta mathcal{L} angle)

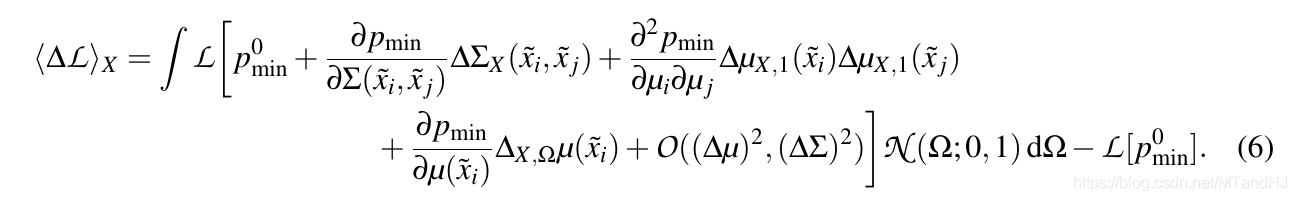
(arg min_X langle mathcal{L} angle_X) 用最小化一阶近似替代, 积分可以用MC积分逼近.

最后给出算法: