CHARACTERIZING ADVERSARIAL SUBSPACES USING LOCAL INTRINSIC DIMENSIONALITY

目录

• 概
• 主要内容
  • LID
  • LID估计
  • 算法
  • 实验
    • 1
  • 2
  • 3
  • 4
  • 5

Ma X, Li B, Wang Y, et al. Characterizing Adversarial Subspaces Using Local Intrinsic Dimensionality[J]. arXiv: Learning, 2018.

@article{ma2018characterizing,
title={Characterizing Adversarial Subspaces Using Local Intrinsic Dimensionality},
author={Ma, Xingjun and Li, Bo and Wang, Yisen and Erfani, Sarah M and Wijewickrema, Sudanthi and Houle, Michael E and Schoenebeck, Grant and Song, Dawn and Bailey, James},
journal={arXiv: Learning},
year={2018}}

概

本文介绍了一种local intrinsic dimensionality(LID)的指标用以揭示普通样本和对抗样本的本质区别, 这个指标可以用用来进行防御(即在样本进来的时候, 提前预判其是否是对抗样本).

主要内容

已有的一些用来区分普通样本和对抗样本的方法, 诸如KD(核密度估计) 和 BU(贝叶斯不确定度, 这个不是很了解), 但是其效果不明显, 本文提出的LID指标能够在各方面胜过他们.
比如在下图中, KM(k均值距离: 取样本(x)到最近的k个样本的距离的平均), 以及核密度估计(KD), 在普通样本和对抗样本上的指标是一致的, 此时无法判断, 而本文的LID的方法却能够判断(LID越大越偏离普通样本).

LID

由一个点为中心, 向外以超距体的方式发散, 其体积(V)与边长(r)的关系可知

[frac{V_2}{V_1} = (frac{r_2}{r_1})^m ightarrow m= frac{log (V_2/V_1)}{ log (r_2 / r_1)}, ]

其中(m)为维度.

于是有人就想出把这种思想推广到一般的数据(数据的分布可能是一个低维的流形)

定义(LID): 给定样本(x in mathcal{X}), 令(R >0)表示(x)到其它样本的距离的随机变量, 并用(F(r))表示概率(P(Rle r)), 且假设其关于(r>0)连续可微, 则在(x)点的距离为(r)的LID定义为

[ ag{2} mathrm{LID}_F(r) := lim_{epsilon ightarrow 0} frac{log (F(1+epsilon)cdot F(r))}{log (1+epsilon)}=frac{rcdot F'(r)}{F(r)}, ]

若极限存在.

注: 最后一个等式成立, 只需中间式子上下同乘(epsilon)再分别取极限即可(既然二者的极限都存在).

最后,

[ ag{3} mathrm{LID}_F := lim_{r ightarrow 0} mathrm{LID}_F(r). ]

此即位我们最后要的LID((r ightarrow 0)是因为我们关注的是局部信息).

LID估计

[ ag{4} widehat{mathrm{LID}}(x)= - (frac{1}{k} sum_{i=1}^k log frac{r_i(x)}{r_k(x)})^{-1}. ]

算法

作者为了利用LID区分对抗样本, 训练了一个分类器. 在预先训练好的网络(H)上, 对每一个样本, 第i层的输出为(H^i(x)), 对每一层的输出, 我们都计算其LID(这一步会用到别的训练数据)并保存下来. 利用这些提取出来的特征(LID), 训练二分类器(作者采用逻辑斯蒂回归).

实验

1

作者首先分析了, 普通样本(normal), 噪声样本(noisy), 对抗样本(adv)的LID指标, 可以发现，LID对对抗样本很敏感, 下面右图分析了在不同层中提取出来的LID值用于区分对抗样本的成功率.

2

比较了不同方法 KD, BU, KD+BU, LID在不同数据下, 对利用不同攻击方法生成的对抗样本进行区分的效果(途中的指标为AUC, AUC指标越大越好)

3

作者在FGM上计算LID并训练分类器, 再用别的方法生成对抗样本, 再测试效果.

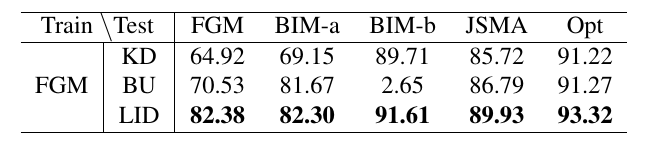
4

作者为了探究每一个batch的大小, 以及超参数(k)的影响, 做了实验, 显然batch size大一点比较好.

5

作者最小化下式生成对抗样本,

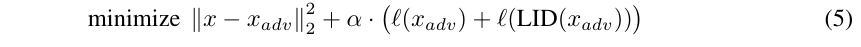
结果这些样本不能够欺骗过LID.

注: 已经别的文章指出, 其成功的原因在于破坏了梯度, 更改一下损失函数就能攻破.