Dynamic Routing Between Capsules

目录

• 概
• 主要内容
  • 损失函数
• 代码

Sabour S, Frosst N, Hinton G E, et al. Dynamic Routing Between Capsules[C]. neural information processing systems, 2017: 3856-3866.

概

虽然11年就提出了capsule的概念, 但是走入人们视线的应该还是这篇文章吧. 虽然现阶段, capsule没有体现出什么优势. 不过, capsule相较于传统的CNN融入了很多先验知识, 更能够拟合人类的视觉系统(我不知), 或许有一天它会大放异彩.

主要内容

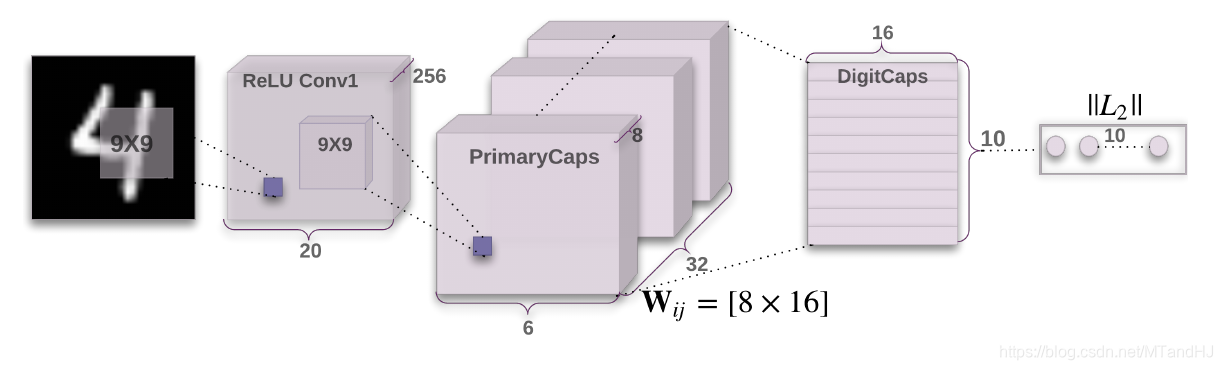
直接从这个结构图讲起吧.

1. Input: 1 x 28 x 28 的图片 经过 9 x 9的卷积核(stride=1, padding=0, out_channels=256)作用;
2. 256 x 20 x 20的特征图, 经过primarycaps作用(9 x 9 的卷积核(strde=2, padding=0, out_channels=256);
3. (32 x 8) x 6 x 6的特征图, 理解为32 x 6 x 6 x 8 = 1152 x 8, 即1152个胶囊, 每个胶囊由一个8D的向量表示(u_{i}); (这个地方要不要squash, 大部分实现都是要的.)
4. 接下来digitcaps中有10个caps(对应10个类别), 1152caps和10个caps一一对应, 分别用(i, j)表示, 前一层的caps为后一层提供输入, 输入为

[hat{u}_{j|i} = W_{ij}u_i, ]

可见, 应当有1152 x 10个(W_{ij}in mathbb{R}^{16 imes 8}), 其中16是输出胶囊的维度. 最后10个caps的输出为

[s_j= sum_{i}c_{ij}hat{u}_{j|i}, v_j= frac{|s|_j^2}{1 + |s_j|^2} frac{s_j}{|s_j|}. ]

其中(c_{ij})是通过一个路由算法决定的, (v_j), 即最后的输入如此定义是出于一种直觉, 即保持原始输出((s))的方向, 同时让(v)的长度表示一个概率(这一步称为squash).

首先初始化(b_{ij}=0) (这里在程序实现的时候有一个考量, 是每一次都要初始化吗, 我看大部分的实现都是如此的).

上面的Eq.3就是

[ ag{3} c_{ij}=frac{exp(b_{ij})}{sum_{k}exp(b_{ik})}. ]

另外(hat{mu}_{j|i} cdot v_j=hat{mu}_{j|i}^Tv_j)是一种cos相似度度量.

损失函数

损失函数采用的是margin loss:

[ ag{4} L_k = T_k max(0, m^+ - |v_k|)^2 + lambda (1 - T_k) max(0, |v_k|-m^-)^2. ]

(m^+, m^-)通常取0.9和0.1, (lambda)通常取0.5.

代码

我的代码, 在sgd下可以训练(但是准确率只有98), 在adam下就死翘翘了, 所以代码肯定是有问题, 但是我实在是找不出来了, 这里有很多实现的汇总.

"""
Sabour S., Frosst N., Hinton G. Dynamic Routing Between Capsules.
Neural Information Processing Systems, pp. 3856-3866, 2017.
https://arxiv.org/pdf/1710.09829.pdf
The implement below refers to https://github.com/adambielski/CapsNet-pytorch.
"""


import torch
import torch.nn as nn
import torch.nn.functional as F



def squash(s):
    temp = s.norm(dim=-1, keepdim=True)
    return (temp / (1. + temp ** 2)) * s


class PrimaryCaps(nn.Module):

    def __init__(
        self, in_channel, out_entities, 
        out_dims, kernel_size, stride, padding
    ):
        super(PrimaryCaps, self).__init__()
        self.conv = nn.Conv2d(in_channel, out_entities * out_dims, 
                            kernel_size, stride, padding)
        self.out_entities = out_entities
        self.out_dims = out_dims

    def forward(self, inputs):
        conv_outs = self.conv(inputs).permute(0, 2, 3, 1).contiguous()
        outs = conv_outs.view(conv_outs.size(0), -1, self.out_dims)
        return squash(outs)


class AgreeRouting(nn.Module):

    def __init__(self, in_caps, out_caps, out_dims, iterations=3):
        super(AgreeRouting, self).__init__()

        self.in_caps = in_caps
        self.out_caps = out_caps
        self.out_dims = out_dims
        self.iterations = iterations

    @staticmethod
    def softmax(inputs, dim=-1):
        return F.softmax(inputs, dim=dim)

    def forward(self, inputs):
        # inputs N x in_caps x out_caps x out_dims
        b = torch.zeros(inputs.size(0), self.in_caps, self.out_caps).to(inputs.device)
        for r in range(self.iterations):
            c = self.softmax(b) # N x in_caps x out_caps !!!!!!!!!
            s = (c.unsqueeze(-1) * inputs).sum(dim=1) # N x out_caps x out_dims
            v = squash(s) # N x out_caps x out_dims
            b = b + (v.unsqueeze(dim=1) * inputs).sum(dim=-1)
        return v



class CapsLayer(nn.Module):

    def __init__(self, in_caps, in_dims, out_caps, out_dims, routing):
        super(CapsLayer, self).__init__()
        self.in_caps = in_caps
        self.in_dims = in_dims
        self.routing = routing
        self.weights = nn.Parameter(torch.rand(in_caps, out_caps, in_dims, out_dims))
        nn.init.kaiming_uniform_(self.weights)

    def forward(self, inputs):
        # inputs: N x in_caps x in_dims
        inputs = inputs.view(inputs.size(0), self.in_caps, 1, 1, self.in_dims)
        u_pres = (inputs @ self.weights).squeeze() # N x in_caps x out_caps x out_dims
        outs = self.routing(u_pres) # N x out_caps x out_dims

        return outs




class CapsNet(nn.Module):

    def __init__(self):
        super(CapsNet, self).__init__()

        # N x 1 x 28 x 28
        self.conv = nn.Conv2d(1, 256, 9, 1, padding=0) # N x (32 * 8) x 20 x 20
        self.primarycaps = PrimaryCaps(256, 32, 8, 9, 2, 0) # N x (6 x 6 x 32) x 8
        routing = AgreeRouting(32 * 6 * 6, 10, 8, 3)
        self.digitlayer = CapsLayer(32 * 6 * 6, 8, 10, 16, routing)


    def forward(self, inputs):
        conv_outs = F.relu(self.conv(inputs))
        pri_outs = self.primarycaps(conv_outs)
        outs = self.digitlayer(pri_outs)
        probs = outs.norm(dim=-1)
        return probs
        


if __name__ == "__main__":

    x = torch.randn(4, 1, 28 ,28)
    capsnet = CapsNet()
    print(capsnet(x))

def margin_loss(logits, labels, m=0.9, leverage=0.5, adverage=True):
    # outs: N x num_classes x dim
    # labels: N
    temp1 = F.relu(m - logits) ** 2
    temp2 = F.relu(logits + m - 1) ** 2
    T = F.one_hot(labels.long(), logits.size(-1))
    loss = (temp1 * T + leverage * temp2 * (1 - T)).sum()
    if adverage:
        loss = loss / logits.size(0)
    # Another implement is using scatter_
    # T = torch.zero(logits.size()).long()
    # T.scatter_(dim=1, index=labels.view(-1, 1), 1.).cuda() if cuda()
    return loss