Boosting Adversarial Training with Hypersphere Embedding

目录

• 概
• 主要内容
• 代码

Pang T., Yang X., Dong Y., Xu K., Su H., Zhu J. Boosting Adversarial Training with Hypersphere Embedding. arXiv preprint arXIv 2002.08619

概

在最后一层, 对weight和features都进行normalize有助于加强对抗训练.

主要内容

一般的神经网络可以用下式表示:

[f(x) = mathbb{S}(W^Tz + b), ]

其中(z=z(x;omega))是encoder部分提取的特征, (W=(W_1, W_2,ldots, W_L), b)分别是最后的权重和偏置, (mathbb{S})表示softmax.

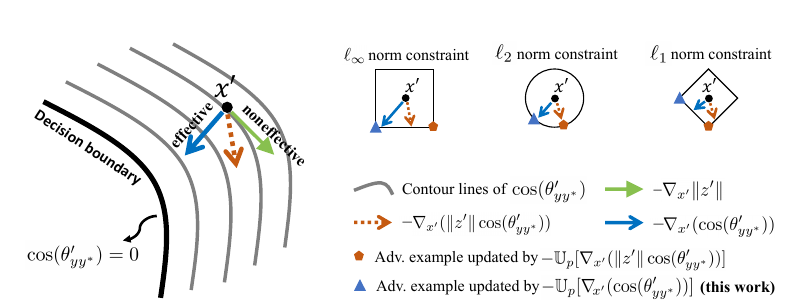
hypersphere embedding (HE):

[widetilde{W}_l = frac{widetilde{W}_l}{|W_l|}, widetilde{z} = frac{z}{|z|} \ widetilde{f}(x) = mathbb{S}(widetilde{W}^Twidetilde{z})=mathbb{S}(cos heta). ]

进一步添加一些margin:

[mathcal{L}_{ce}^m (widetilde{f}(x), y) = -1_y^T log mathbb{S}(scdot (cos heta -m cdot mathbb{1}_y)). ]

为什么要这么做呢? 作者觉得, 生成对抗样本最有效的途径是旋转角度, 即图中的蓝线. 如果你不限制(z)或者(W), 那么梯度会同时在模的大小的上下功夫, 这并不高效.

代码

原文代码