Zhao J., Mathieu M. & LeCun Y. Energy-based generative adversarial networks. ICLR, 2017.
概
基于能量的一个解释.
主要内容
本文采用了与GAN不同的损失, 判别器(D)和生成器(G)分别最小化下面的损失:
[mathcal{L}_D (x, z) = D(x) + [m-D(G(z))]^+ \
mathcal{L}_G(z) = D(G(z))
]
需要注意的是, 这里的判别器(D)的输出已经不是普通GAN中判别器的真假概率了, 而是能量, 能量越低,即(D(x))越小, 越真.
用(V(G, D)= int_{x, z} mathcal{L}_D(x, z) p_{data}(x) p_g(z) mathrm{d}xmathrm{d}z), 用(U(G,D) = int_{z} mathcal{L}_G(z) p_g(z)mathrm{d}z), 考虑如下纳什均衡
[V(G^*, D^*) le V(G^*, D), quad forall D \
U(G^*, D^*) le U(G, D^*), quad forall G.
]
第一个需要考虑的问题是, 这样的纳什均衡解会有什么好的性质呢?
定理1: ((G^*, D^*))为纳什均衡解, 则(p_{G^*}=p_{data}, : a.e.), (V(G^*, D^*)=m).
proof:
[V(G, D) = int_{x} D(x) p_{data} (x)mathrm{d}x + int_z [m-D(G(z))]^+ p_G(z) mathrm{d}z = int_{x} D(x) p_{data} (x)mathrm{d}x + int_x [m-D(x)]^+ p_G(x) mathrm{d}x.
]
故需要考虑
[min quad D(x) p_{data}(x) + [m-D(x)]^+ p_{G^*}(x),
]
可得
[D(x) = left {
egin{array}{ll}
m, & p_{data} < p_{G^*} \
0, & p_{data} > p_{G^*} \
[0, m], & else.
end{array}
ight.
]
所以
[egin{array}{ll}
V(G^*, D^*) & = int_{p_{data} < p_{G^*}} m p_{data}(x) mathrm{d}x + int_{p_{data} > p_{G^*}} mp_{G^*}(x)mathrm{d}x + int_{p_{data}=p_{G^*}} G^*(x) p_{data}(x) mathrm{d}x \
& le m + m int_{p_{data} < p_{G^*}} m [p_{data}(x) - p_{G^*}(x)] mathrm{d}x le m.
end{array}
]
另一方面,
[U(G,D^*) = int_x D^*(x) p_{G}(x) mathrm{d} x ge int_{x} D^* (x) p_{G^*}(x) mathrm{d}x
]
所以
[V(G^*, D^*) ge int_x (D^*(x) + [m-D^*(x)]^+)p_{G^*}(x) mathrm{d}x ge m.
]
所以(V(G^*, D^*)=m), 且(p_{G^*}=p_{data}, : a.e.)
下一个问题是, 这个纳什均衡存在吗, 文中的定理二给出了这个答案, 不过需要一个额外的条件, 这里不多赘述.
文中最后采用的是下面的框架:
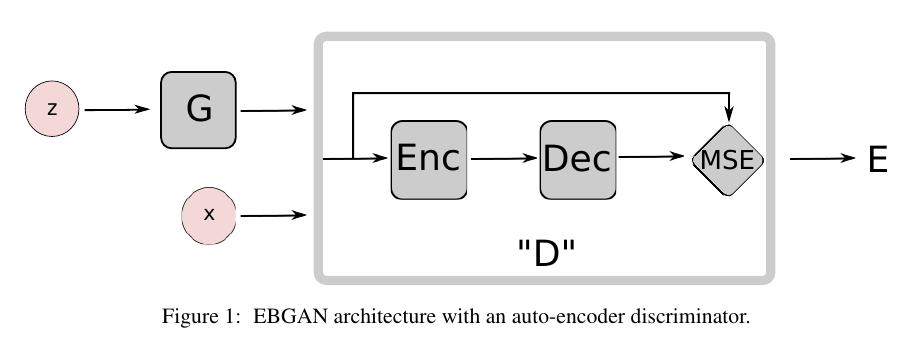
即能量函数(D)的选择为
[D(x) = |Dec(Enc(x)) - x|.
]