概
CAM (class activation mapping) 是一种非常实用的可视化方法, 同时在弱监督学习中(如VQA)起了举足轻重的作用.
主要内容
CAM的概念, 用于解释, 为什么神经网络能够这么有效, 而它究竟关注了什么?
| 符号 | 说明 |
|---|---|
| (f(cdot)) | 网络 |
| (X) | 网络输入 |
| (A_l^k) | 第(l)层的第(k)张特征图(特指在卷积层中) |
| (w) | 权重 |
| (c) | 所关心的类别 |
| (alpha) | 用于CAM的权重 |
CAM
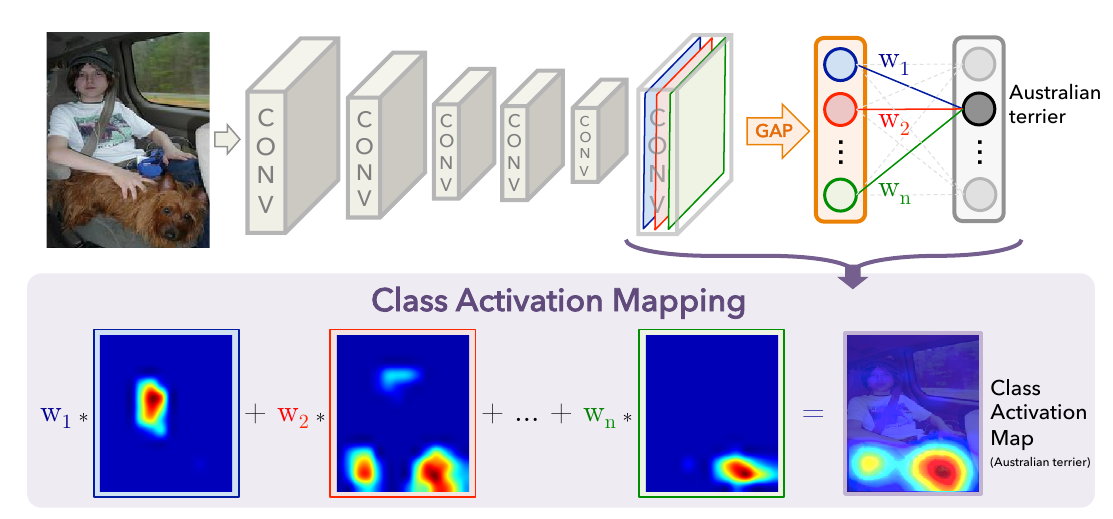
最开始的CAM仅用于特殊的CNN: 卷积层 + AvgPool + FC的结构,
设最后一层卷积层的特征图为(A_L), 则
[f_c(X) = {w^c}^T GP(A_L), [GP(A_L)]_k = frac{1}{HW}sum_i^H sum_j^W [A_L^k]_{ij}, k=1,cdots, K.
]
进一步可以注意到,
[f_c(X) = frac{1}{HW} sum_i^H sum_j^W [sum_{k=1}^K w_k^c [A_L^k]_{ij}].
]
于是可以定义:
[[L_{CAM}^c]_{ij} = sum_{k=1}^K alpha_k^c [A_L^k]_{ij}, quad i=1,cdots H, j=1,cdots, W.
]
这里, (alpha = frac{w}{HW}).
即
[L_{CAM}^c = sum_{k=1}^K alpha_k^c A_L^k.
]
一般, 这种score会最后加个relu:
[L_{CAM}^c = mathrm{ReLU}(sum_{k=1}^K alpha_k^c A_L^k).
]
Grad-CAM
普通的CAM有限制, Grad-CAM在此基础上进行扩展.
[L_{Grad-CAM}^c = mathrm{ReLU}(sum_{k=1}^K alpha_k^c A_l^k),
]
[alpha_k^c = GP(frac{partial f^c}{partial A_l^k})=frac{1}{HW}sum_i sum_j frac{partial f_c}{partial [A_l^k]_{ij}}.
]
注意: (L ightarrow l).
Grad-CAM++
作者认为, Grad-CAM++不能很好应对多个目标的情况, 应该进一步加权:
[alpha_k^c = frac{1}{HW} sum_i sum_j alpha_{ij}^{kc} mathrm{ReLU}(frac{partial f_c}{partial [A_{l}^k]_{ij}}),
]
[alpha_{ij}^{kc}=frac{frac{partial^2 f_c}{(partial[A_{l}^k]_{ij})^2}}{2frac{partial^2 f_c}{(partial[A_{l}^k]_{ij})^2}+sum_isum_j[A_l^k]_{ij}frac{partial^3 f_c}{(partial[A_{l}^k]_{ij})^3}}.
]
Score-CAM
作者认为, 利用梯度计算score并不是一个很好的主意.
[alpha_k^c = f_c(X circ H_l^k) - f(X_b),
]
这里(X_b)是一个固定的基准向量, 作者直接取(f(X_b)=mathbb{0}),
[H_l^k = s(Up(A_l^k)),
]
为将(A_l^k)上采样至和(X)相同大小, 并标准化:
[s(M) = frac{M - min M}{max M - min M},
]
使其落于([0, 1]).
最后
(L^c_*)最后也只是(H imes W)的, 需要上采样到和(X)一样的大小.