概
隐变量的因果表示.
主要内容
我们通常希望隐变量(z)能够表示一些特别的特征, 通过改变(z)使得生成的图形某些属性发生相应的变换, 但是这种设定的方式并不具备因果的关系, 比方说
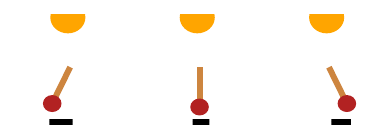
这个摆锤, 其隐变量(z)是光照, 摆锤的角度, 影子的长短.
我们可以改变摆锤的角度, 一般的生成模型摆锤的角度变了, 但是光照和影子长短没有发生变化, 实际上由于摆锤角度的变化, 对于的隐变量:影子的长短也应该发生相应的变化以满足物理的规律. 如何把这些因果关系融入到普通的VAE中是本文的独到之处.
模型
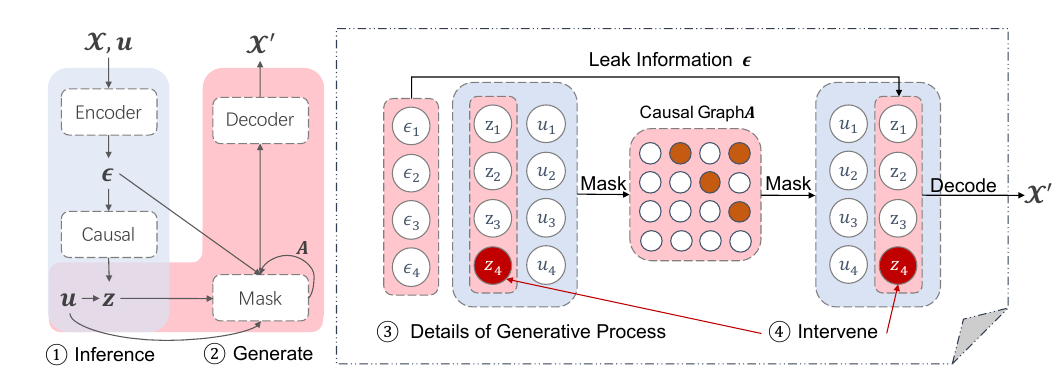
Encoder 部分:
[epsilon = h(x, u) + zeta,
]
(epsilon)可以看成是一个临时的隐变量;
[z = (I - A)^{-1} epsilon.
]
Decoder部分:
[z_i = g_i(A_i circ z) + epsilon_i,
]
这一部分是重构(z), 正是这一步的存在使得我们能够干预(z_i)使得其它的(z_j)也发生相应的改变.
[x = f(z) + xi.
]
联合分布为:
[p_{ heta}(x, z, epsilon|u) = p_{ heta}(x|z, epsilon, u)p_{ heta}(epsilon, z|u), \
p_{ heta}(x|z,epsilon,u) = p_{ heta}(x|z) = p_{xi}(x-f(z)), \
p_{ heta}(epsilon,z|u) = p_{epsilon}(epsilon) p_{ heta}(z|u), quad p_{epsilon}(epsilon) = mathcal{N}(0, I), \
p_{ heta}(z|u) = prod_{i=1}^n p_{ heta}(z_i|u_i), quad p_{ heta}(z_i|u_i) = mathcal{N}(lambda_1(u_i), lambda_2^2(mu_i)).
]
估计的后验分布为:
[q_{phi}(z, epsilon|x, u) = q(z|epsilon)q_{zeta}(epsilon - h(x, u)), \
q(z|epsilon) = delta (z=(I-A)^{-1}epsilon).
]
注: (z, u, epsilon in mathbb{R}^n, x in mathbb{R}^d.)
ELBO
由此可以推出ELBO:
[mathbb{E}_{q_{mathcal{X}}}[mathbb{E}_{epsilon, zsim q_{phi}}[log p_{ heta}(x| z, epsilon,u)] - mathbb{D}(q_{phi}(epsilon, z|x, u))| p_{ heta}(epsilon, z|u)].
]
由于(p(z|epsilon) = delta(z=(I-A)^{-1}epsilon)), 所以上式可以进一步化为:
[mathbb{E}_{q_{mathcal{X}}}[mathbb{E}_{q_{phi(z|x,u)}}[log p_{ heta}(x|z)] - mathbb{D}(q_{phi}(epsilon|x,u)|p_{epsilon}(epsilon))-mathbb{D}(q_{phi}(z|x,u)|p_{ heta}(z|u))]+mathrm{const}.
]
关于(A)
正如在这儿所论述的, (A)需要对应一个有向无环图, 本文采取的策略是:
[H(A) = mathrm{tr}((I+frac{c}{n}A circ A)^n) - n =0,
]
这里(c)是任意正数.
同时为了满足(z)重构, 需要以下条件满足:
[l_m = mathbb{E}_{q_{phi}} sum_{i=1}^n |z_i-g_i(A_i circ z)|^2 le kappa_2,
]
注: 这里(z_i)是重构前的.
特别的, 为了更好地用额外信息(不是很认同, 感觉得看实际情况吧):
[l_u = mathbb{E}_{q_{mathcal{X}}} |u - sigma(A^Tu)|_2^2 le kappa_1,
]
所以最终的损失为:
[mathcal{L} = -mathrm{ELBO} +alpha H(A) + eta l_u + gamma l_m,
]
注: 本文不像别的方法一样用augmented Lagrange 求解.
注: 作者设计的实验实在是非常有趣.