1252. Cells with Odd Values in a Matrix

There is an m x n matrix that is initialized to all 0's. There is also a 2D array indices where each indices[i] = [ri, ci] represents a 0-indexed location to perform some increment operations on the matrix.

For each location indices[i], do both of the following:

1. Increment all the cells on row ri.
2. Increment all the cells on column ci.

Given m, n, and indices, return the number of odd-valued cells in the matrix after applying the increment to all locations in indices.

Example 1:

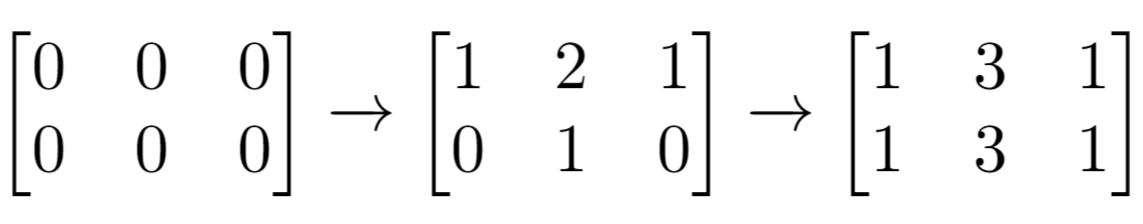
Input: m = 2, n = 3, indices = [[0,1],[1,1]]
Output: 6
Explanation: Initial matrix = [[0,0,0],[0,0,0]].
After applying first increment it becomes [[1,2,1],[0,1,0]].
The final matrix is [[1,3,1],[1,3,1]], which contains 6 odd numbers.

Constraints:

• 1 <= m, n <= 50
• 1 <= indices.length <= 100
• 0 <= ri < m
• 0 <= ci < n

• class Solution {
  public:
      int oddCells(int m, int n, vector<vector<int>>& indices) {
          vector<int> r(m); 
          vector<int> c(n);
          int ans=0;
          for(auto &idx:indices){
              r[idx[0]]^=1;
              c[idx[1]]^=1;
          }
          for(int i=0;i<m;++i)
              for(int j=0;j<n;j++)
                  ans+=r[i]^c[j];
          return ans;  
      }
  };

  以上代码参考 花花酱 。异或运算(^) ，两个相同则为假，两个不同则为真。每一行或一列的数都当成整体操作。0与1进行异或运算偶数次结果为0，奇数次异或操作结果为0