题目
题目描述
Bytetown城市要进行市长竞选,所有的选民可以畅所欲言地对竞选市长的候选人发表言论。为了统一管理,城市委员会为选民准备了一个张贴海报的electoral墙。
张贴规则如下:
-
electoral墙是一个长度为N个单位的长方形,每个单位记为一个格子;
-
所有张贴的海报的高度必须与electoral墙的高度一致的;
-
每张海报以“A B”表示,即从第A个格子到第B个格子张贴海报;
-
后贴的海报可以覆盖前面已贴的海报或部分海报。
现在请你判断,张贴完所有海报后,在electoral墙上还可以看见多少张海报。
输入格式
第一行: N M 分别表示electoral墙的长度和海报个数
接下来M行: Ai Bi 表示每张海报张贴的位置
输出格式
输出贴完所有海报后,在electoral墙上还可以看见的海报数。
输入输出样例
输入 #1
100 5 1 4 2 6 8 10 3 4 7 10
输出 #1
4
说明/提示

注:图片来源:洛谷
【约束条件】
1 0<= N <= 10000000 1<=M<=1000 1<= Ai <= Bi <=10000000
所有的数据都是整数。数据之间有一个空格
分析
还有一种方法:浮水法:题解 P3740 【[HAOI2014]贴海报】
一个很妙的逆向思维
如果正向思考,覆盖的时候绞尽脑汁消除覆盖,很麻烦
看最后露出来的,只要前面没挡到,就会露出来,例如:

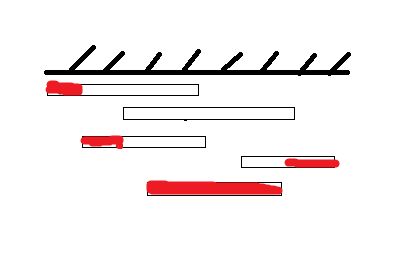
可以存入空白,倒向操作,只要覆盖了空白的海报,就会露出来
但在离散化的时候会出错,比如:
8 3
3 6
1 3
6 7
本来是:
离散化后3与6相邻,答案本应3,输出为2,变成了:

解决方法:在离散化时,不是消去中间,而是将中间距离大于1的变为1
注意数组大小
代码

1 /************************** 2 User:Mandy.H.Y 3 Language:c++ 4 Problem:luogu3740 5 Algorithm:线段树 + 离散化 6 **************************/ 7 8 // 一个很妙的逆向思维 9 //如果正向思考,覆盖的时候绞尽脑汁消除覆盖,很麻烦 10 //看最后露出来的,只要前面没挡到,就会露出来 11 //可以存入空白,倒向操作,只要覆盖了空白的海报,就会露出来 12 //但在离散化的时候会出错,比如: 13 //8 3 14 //3 6 15 //1 3 16 //6 7 17 //离散化后3与6相邻,答案本应3,输出为2 18 //解决方法:在离散化时,不是消去中间,而是将中间距离大于1的变为1 19 //注意数组大小 20 21 22 #include<bits/stdc++.h> 23 #define Max(x,y) ((x) > (y) ? (x) : (y)) 24 #define Min(x,y) ((x) < (y) ? (x) : (y)) 25 #define lson l,mid,k<<1 26 #define rson mid + 1,r,k<<1|1 27 28 using namespace std; 29 30 const int maxm = 2005; 31 int n,m,ans,judge = 0; 32 int tree[maxm << 4]; 33 34 struct Poster{ 35 int l,r; 36 }pos[maxm]; 37 38 struct Temp{ 39 int l,id; 40 bool operator < (const Temp &a)const { 41 return l < a.l; 42 } 43 }tmp[maxm << 1]; 44 45 template<class T>inline void read(T &x) { 46 x = 0;bool flag = 0;char ch = getchar(); 47 while(!isdigit(ch)) flag |= ch == '-',ch = getchar(); 48 while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar(); 49 if(flag) x = -x; 50 } 51 52 template<class T>void putch(const T x) { 53 if(x > 9) putch(x / 10); 54 putchar(x % 10 | 48); 55 } 56 57 template<class T>void put(const T x) { 58 if(x < 0) putchar('-'),putch(-x); 59 else putch(x); 60 } 61 62 void file() { 63 freopen("3740.in","r",stdin); 64 // freopen("2161.out","w",stdout); 65 } 66 67 void readdata() { 68 read(n);read(m); 69 } 70 71 void pushup(int k){ 72 tree[k] = tree[k<<1] + tree[k<<1|1]; 73 } 74 75 void pushdown(int k){ 76 if(!tree[k]){ 77 tree[k<<1] = 0; 78 tree[k<<1|1] = 0; 79 }//标记下放 80 } 81 82 void buildtree(int l,int r,int k){ 83 if(l == r){ 84 tree[k] = 1; 85 return; 86 } 87 int mid = (l + r) >> 1; 88 buildtree(lson); 89 buildtree(rson); 90 pushup(k); 91 } 92 93 void modify(int l,int r,int k,int x,int y){ 94 if(x <= l && r <= y){ 95 if(tree[k]) judge = 1; 96 tree[k] = 0; 97 return; 98 } 99 pushdown(k); 100 int mid = (l + r) >> 1; 101 if(x <= mid) modify(lson,x,y); 102 if(y > mid) modify(rson,x,y); 103 pushup(k); 104 } 105 106 void work() { 107 int cnt = 0; 108 for(int i = 1;i <= m ; ++ i){ 109 read(tmp[++cnt].l);tmp[cnt].id = i; 110 read(tmp[++cnt].l);tmp[cnt].id = i; 111 } 112 113 sort(tmp + 1,tmp + cnt + 1); 114 int tot = 0;//去重 及 变为1 115 for(int i = 1;i <= cnt; ++ i){ 116 int id = tmp[i].id; 117 if(tmp[i].l != tmp[i - 1].l){ 118 if(tmp[i].l - tmp[i - 1].l > 1) ++tot; 119 if(pos[id].l) pos[id].r = ++tot; 120 else pos[id].l = ++tot; 121 } else { 122 if(pos[id].l) pos[id].r = tot; 123 else pos[id].l = tot; 124 } 125 126 } 127 128 buildtree(1,tot,1); 129 130 for(int i = m;i >= 1; -- i){ 131 judge = 0; 132 modify(1,tot,1,pos[i].l,pos[i].r); 133 if(judge) ans++; 134 } 135 put(ans); 136 } 137 138 int main() { 139 // file(); 140 readdata(); 141 work(); 142 return 0; 143 }
