P1002 过河卒
题目描述
棋盘上 A 点有一个过河卒,需要走到目标 B 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,A 点 (0, 0)、B 点 (n, m),同样马的位置坐标是需要给出的。
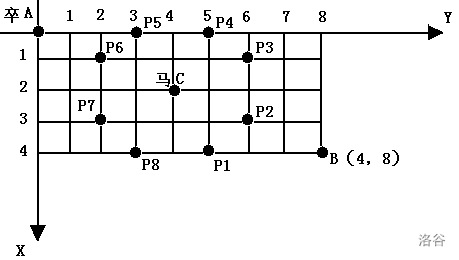
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入格式
一行四个正整数,分别表示 B 点坐标和马的坐标。
输出格式
一个整数,表示所有的路径条数。
输入输出样例
输入 #1 输出 #1
6 6 3 3 6
说明/提示
对于 100% 的数据,1≤n,m≤20,0≤ 马的坐标 ≤20。
解题思路:抓住题目的关键,我们要求的是卒从原点走到B点的路径数目,很显然是一个动态规划的题目,我们开一个dp数组
因为卒只有两种走法,那么我们可以将问题拆分,dp[i][j]的走法就等于dp[i-1][j]+dp[i][j-1]的走法,因为卒只能向下走或者向右走
但是这里需要注意,由于原点是从0,0开始的,所以i-1,j-1可能数组越界,又由于存在一个马在挡路,分析可知,马的坐标和几个控制点的坐标是走不通的
也就是说如果卒走到了马的控制点或者马的坐标的时候,方案数就为0,那么我们就能得到状态转移方程:
if(judge(i,j)) { if(i) dp[i][j]+=dp[i-1][j]; if(j) dp[i][j]+=dp[i][j-1]; } else dp[i][j]=0;
AC代码如下:
#include<bits/stdc++.h> #define ll unsigned long long #pragma-GCC-optimize("-Ofast"); using namespace std; ll a1,b1,a2,b2; ll dp[30][30],dx[8]={-1,-2,-2,-1,1,2,2,1},dy[8]={-2,-1,1,2,2,1,-1,-2}; ll judge(ll x,ll y)//判断是否走到马的坐标或者控制点的坐标 { if(x==a2&&y==b2) return 0; for(ll i=0;i<8;++i) { ll nx=a2+dx[i]; ll ny=b2+dy[i]; if(nx>=0&&nx<=a1&&ny>=0&&ny<=b1&&nx==x&&ny==y) { return 0; } } return 1; } int main(void) { ios::sync_with_stdio(false); cin>>a1>>b1>>a2>>b2; dp[0][0]=(ll)1; for(ll i=0;i<=a1;++i) { for(ll j=0;j<=b1;++j) { if(judge(i,j)) { if(i)//防止i为0的情况,数组越界 dp[i][j]+=dp[i-1][j]; if(j)//防止j为0的情况,数组越界 dp[i][j]+=dp[i][j-1]; } else dp[i][j]=0;//走到了马的坐标或者控制点的坐标 } } cout<<dp[a1][b1]<<endl; return 0; }