题目链接:传送门
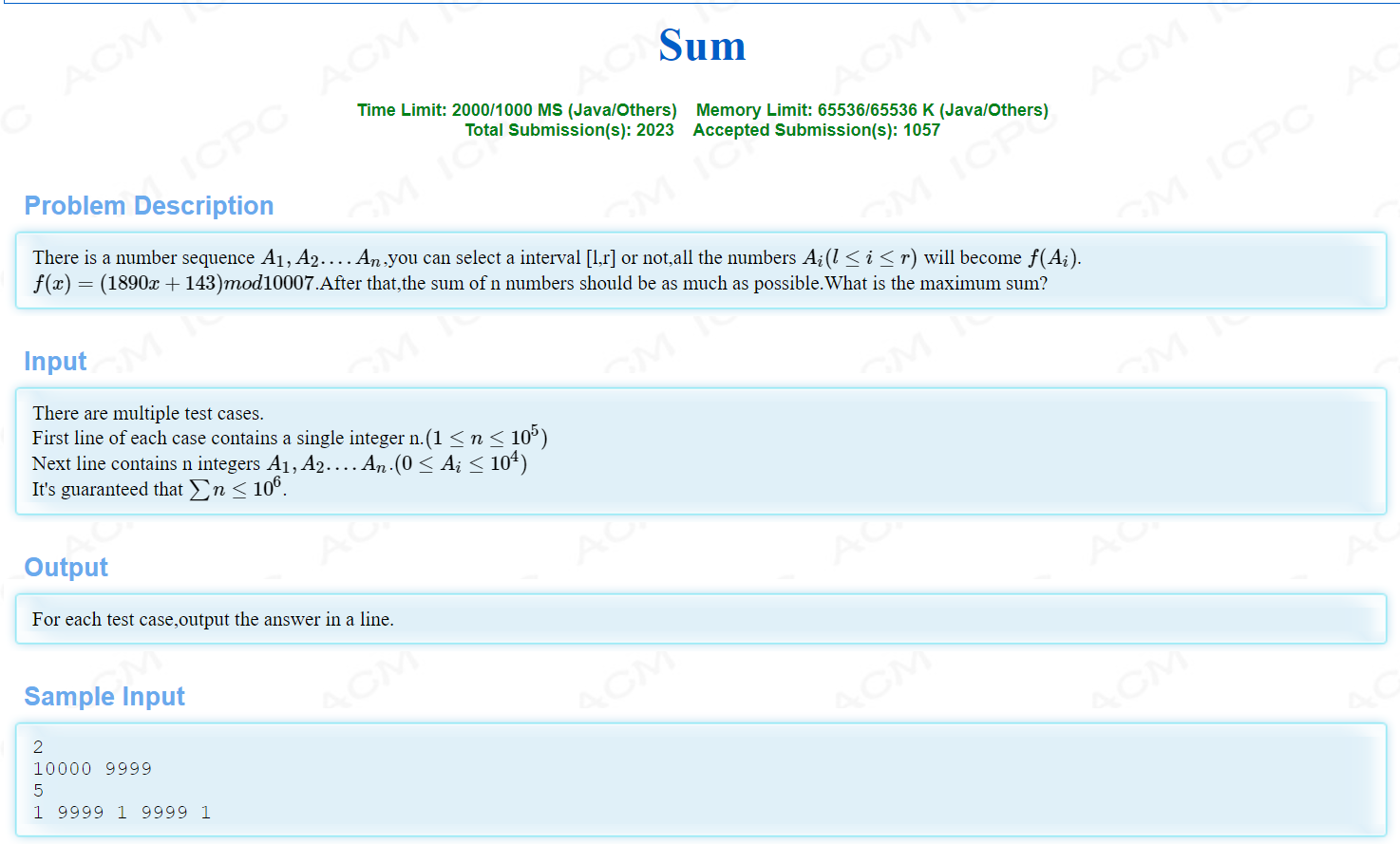
题意:给你n个数字,然后你可以对这n个数组的任意一个子区间进行一个操作,(f(x)=(1890x+143)mod10007),或者不进行操作,问你怎样操作能使得加和最大
解题思路:我们通过预处理a数组元素,把改数字操作后的值和操作前的值进行一个做差存储在b数组里面,此时问题便转化为了求解b数组连续的子序列的和的值,当然如果b数组连续子序列和的值小于0,我们就不对a数组的元素进行任何操作,dp[i]表示的是长度为i的连续序列的最大值,动态转移方程为:(dp[i] = max(dp[i-1],max_))
Code:
#include<bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f, N = 100005, mod = 10007;
int n,a[N],b[N],dp[N];
int main()
{
while(~scanf("%d",&n)) {
int sum = 0;
for(int i = 1; i <= n; ++i) {
scanf("%d",&a[i]);
sum += a[i];
b[i] = (1890 * a[i] + 143) % mod - a[i];//预处理差值
}
int max_ = 0;
dp[0] = 0;
for(int i = 1;i <= n; ++i) {
max_ += b[i];
if(max_ < 0) {//如果小于0则更新max_的值
max_ = 0;
}
dp[i] = max(dp[i-1],max_);
}
printf("%d
",sum + max(0,dp[n]));
}
return 0;
}