二叉树部分的常见算法与实现

二叉树

二叉树的遍历非常重要，一定要熟练掌握。

• 因为二叉树的层序创建，层序遍历均用到了队列结构，二叉树的非递归遍历用到了堆栈结构，这部分的代码在后面单独给出。
• 二叉树的后序非递归遍历有两种实现思路，在下面的代码中只实现了一种。

二叉树的链表结构为：

struct TNode
{
    int Data;  //节点的数据
	struct TNode* Left;  //指向左子树
	struct TNode* Right;  //指向右子树
};

typedef struct TNode* ElementType;

二叉树部分的算法与相关代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include"queue.h"
#include"Stack.h"
#define NoInfo 0  //用0表示没有节点

//struct TNode
//{
//	int Data;  //节点的数据
//	struct TNode* Left;  //指向左子树
//	struct TNode* Right;  //指向右子树
//};

//作用：层序生成二叉树
struct TNode* CreatBinTree()
{
	int Data;
	struct QNode* Q = CreatQueue(10);  //创建空队列
	struct TNode* T;
	struct TNode* BT;

	//建立第一个节点，即根节点
	scanf("%d",&Data);
	if (Data != NoInfo)
	{
		//动态分配一个结点单元，并存入数据，同时将该结点地址放入队列
		BT = (struct TNode *)malloc(sizeof(struct TNode));
		BT->Data = Data;
		BT->Left = NULL;
		BT->Right = NULL;
		AddQ(Q,BT);
	}
	else
	{
		return NULL;
	}

	while (!IsEmpty(Q))
	{
		T = DeleteQ(Q);  //从队列中取出一节点地址
		scanf("%d",&Data);
		if (Data != NoInfo)
		{
			//动态分配一个结点单元，并存入数据，同时将该结点地址放入队列
			T->Left = (struct TNode *)malloc(sizeof(struct TNode));
			T->Left->Data = Data;
			T->Left->Left = NULL;
			T->Left->Right = NULL;
			
			AddQ(Q, T->Left);
		}
		else
		{
			T->Left = NULL;
		}
		//读入右孩子的数据
		scanf("%d", &Data);
		if (Data != NoInfo)
		{
			//动态分配一个结点单元，并存入数据，同时将该结点地址放入队列
			T->Right = (struct TNode *)malloc(sizeof(struct TNode));
			T->Right->Data = Data;
			T->Right->Left = NULL;
			T->Right->Right = NULL;

			AddQ(Q, T->Right);
		}
		else
		{
			T->Right = NULL;
		}	
	} //end while (!IsEmpty(Q))
	return BT;
}
//作用：二叉树的递归后序遍历
void PostorderTraversal(struct TNode* BT)
{
	if (BT)
	{
		PostorderTraversal(BT->Left);
		PostorderTraversal(BT->Right);
		printf("%d. ", BT->Data);
	}
}
//作用：二叉树的递归先序遍历
void PreorderTraversal(struct TNode* BT)
{
	if (BT)
	{
		printf("%d. ", BT->Data);
		PreorderTraversal(BT->Left);
		PreorderTraversal(BT->Right);
	}
}
//作用：二叉树的递归中序遍历
void InorderTraversal(struct TNode* BT)
{
	if (BT)
	{
		InorderTraversal(BT->Left);
		printf("%d. ", BT->Data);
		InorderTraversal(BT->Right);
	}
}
//作用：二叉树的非递归中序遍历
void InorderTraversal2(struct TNode* BT)
{
	struct TNode* T;

	struct SNode* S = CreatStack(10);

	T = BT;
	
	while (T || !IsStackEmpty(S))
	{
		while (T)
		{
			Push(S, T);
			T = T->Left;
		}
		T = Pop(S);
		printf("%d. ",T->Data);
		T = T->Right;  //转向右子树
	}
}
//作用：二叉树的非递归先序遍历
void PreorderTraversal2(struct TNode* BT)
{
	struct TNode* T;

	struct SNode* S = CreatStack(10);

	T = BT;

	while (T || !IsStackEmpty(S))
	{
		while (T)
		{
			printf("%d. ", T->Data);
			Push(S, T);
			T = T->Left;
		}
		T = Pop(S);
		T = T->Right;  //转向右子树
	}
}
//作用：二叉树的非递归后序遍历
//思路1 将先序遍历的算法进行更改
void PostorderTraversal2(struct TNode* BT)
{
	struct TNode* T;

	struct SNode* S1 = CreatStack(10);
	struct SNode* S2 = CreatStack(10);

	T = BT;

	while (T || !IsStackEmpty(S1))
	{
		while (T)
		{
			//printf("%d. ", T->Data);
			Push(S2, T);  //压入根节点
			Push(S1, T);
			T = T->Right;
		}
		T = Pop(S1);
		T = T->Left;  //转向左子树
	}
	while (!IsStackEmpty(S2))
	{
		T = Pop(S2);
		printf("%d. ",T->Data);
	}
}
//作用：二叉树的非递归后序遍历
//思路2 
//ToDo: 参考博客园博客，这里有一个思路2还没有写
void PostorderTraversal3(struct TNode* BT)
{



}
//作用：层序遍历
void LevelorderTraversal(struct TNode* BT)
{
	struct QNode* Q;
	struct TNode* T;
	if (!BT)
	{
 		return;  //若是空树，直接返回
	}
	Q = CreatQueue(10);
	AddQ(Q, BT);  //首先将根节点入队

	while (!IsEmpty(Q))
	{
		T = DeleteQ(Q);
		printf("%d. ", T->Data);
		if (T->Left != NULL)
		{
			AddQ(Q, T->Left);
		}
		if (T->Right != NULL)
		{
			AddQ(Q,T->Right);
		}
	}

}
//作用:输出二叉树的叶子结点
void PreorderPrintLeaves(struct TNode* BT)
{
	if (BT)
	{
		if (BT->Left == NULL && BT->Right == NULL)
		{
			printf("%d. ", BT->Data);
		}
		PreorderPrintLeaves(BT->Left);
		PreorderPrintLeaves(BT->Right);
	}
}
//作用:求二叉树的高度
int GetHeight(struct TNode* BT)
{
	int HL;
	int HR;
	int MaxH;
	if (BT)  //BT非空进行遍历
	{
		HL = GetHeight(BT->Left);
		HR = GetHeight(BT->Right);
		MaxH = HL > HR ? HL : HR;
		 return MaxH + 1;
	}
	else
	{
		return 0;
	}
	
}
int main()
{
	struct TNode* BT = CreatBinTree();
	printf("中序递归遍历:
");
	InorderTraversal(BT);
	printf("
先序递归遍历:
");
	PreorderTraversal(BT);
	printf("
后序递归遍历:
");
	PostorderTraversal(BT);

    printf("
非递归中序遍历:
");
	InorderTraversal2(BT);
	printf("
非递归先序遍历:
");
	PreorderTraversal2(BT);
	printf("
非递归后序遍历:
");
	PostorderTraversal2(BT);
	printf("
层序遍历
");
	LevelorderTraversal(BT);
	printf("
输出二叉树中所有的叶子结点
");
	PreorderPrintLeaves(BT);
	printf("二叉树的高度: %d.
", GetHeight(BT));
	system("pause");
	return 0;
}

实现链表部分的代码：

queue.h

//二叉树的创建需要队列
//该文件实现队列的一系列操作
#pragma once
#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>

struct TNode
{
	int Data;  //节点的数据
	struct TNode* Left;  //指向左子树
	struct TNode* Right;  //指向右子树
};

typedef struct TNode* ElementType;

struct QNode 
{
	ElementType* Data;  //存储元素的数组
	int Front;  //队列的头指针
	int Rear;  //队列的尾指针
	int MaxSize;  //队列的最大容量
};

struct QNode* CreatQueue(int MaxSize);
bool IsFull(struct QNode* Q);
bool AddQ(struct QNode* Q, ElementType x);
bool IsEmpty(struct QNode* Q);
ElementType DeleteQ(struct QNode* Q);

queue.c

#include<stdio.h>
#include"queue.h"
//作用：创建一个队列
//参数：队列的大小
struct QNode* CreatQueue(int MaxSize)
{
	struct QNode* Q = (struct QNode *)malloc(sizeof(struct QNode));
	Q->Data = (ElementType *)malloc(MaxSize * sizeof(int));
	Q->Front = Q->Rear = 0;
	Q->MaxSize = MaxSize;
	return Q;
}
//作用：判断当前队列是否满
//参数：待判断的队列
bool IsFull(struct QNode* Q)
{
	return ((Q->Rear + 1) % Q->MaxSize == Q->Front);
}
//作用：向队列中插入元素
//参数：struct QNode* Q 待插入的队列
//      int x 待插入的元素
bool AddQ(struct QNode* Q, ElementType x)
{
	if (IsFull(Q))  //判断队列是否为空
	{
		printf("队列满，不能再插入元素
");
		return false;
	}
	else
	{
		Q->Rear = (Q->Rear + 1) % Q->MaxSize;
		Q->Data[Q->Rear] = x;
		return true;
	}
}
//作用：判断队列是否为空
//参数：
//返回值： true   空
//         false  非空
bool IsEmpty(struct QNode* Q)
{
	return (Q->Front == Q->Rear);
}
//作用：
//参数：
ElementType DeleteQ(struct QNode* Q)
{
	if (IsEmpty(Q))
	{
		printf("队列为空
");
		return NULL;
	}
	else
	{
		Q->Front = (Q->Front + 1) % Q->MaxSize;
		return Q->Data[Q->Front];
	}
}

实现堆栈部分的代码：

Stack.h

#pragma once
#include<stdbool.h>
#include"queue.h"

struct SNode
{
	ElementType* Data;  //存储元素的数组
	int Top;  //栈顶指针
	int MaxSize;  //堆栈的最大容量
};

struct SNode* CreatStack(int MaxSize);
bool IsStackFull(struct SNode* S);
bool Push(struct SNode* S,ElementType x);
bool IsStackEmpty(struct SNode* S);
ElementType Pop(struct SNode* S);

Stack.c

#include"Stack.h"
#include<stdlib.h>

struct SNode* CreatStack(int MaxSize)
{
	struct SNode* S = (struct SNode *)malloc(sizeof(struct SNode));
	S->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
	S->MaxSize = MaxSize;
	S->Top = -1;
	return S;
}
//作用：判断当前堆栈是否满
//返回值： ture 当前堆栈满
//         false 当前堆栈非满
bool IsStackFull(struct SNode* S)
{
	return S->Top == S->MaxSize - 1;
}
bool Push(struct SNode* S, ElementType x)
{
	if (IsStackFull(S))
	{
		printf("当前堆栈已满.
");
		return false;
	}
	else
	{
		S->Top = S->Top + 1;
		S->Data[S->Top] = x;
		return true;
	}

}
//作用:判断当前堆栈是否为空
//返回值：true 空
//        false 非空
bool IsStackEmpty(struct SNode* S)
{
	return S->Top == -1;

}
ElementType Pop(struct SNode* S)
{
	if (IsStackEmpty(S))
	{
		printf("堆栈为空.
");
		return false;
	}
	else
	{
		return S->Data[(S->Top)--];
	}
}

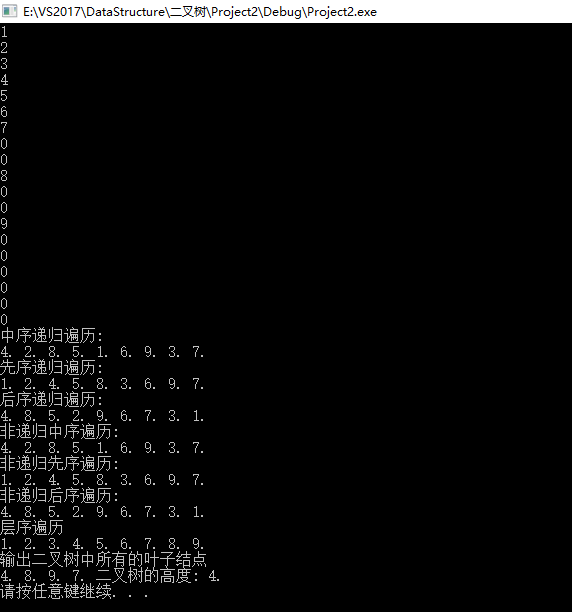
运行结果：