- 题目来源:
浙江大学在慕课网上开设的《数据结构》课,陈越老师、何钦铭老师主讲,课后作业的一道题。
-
题目描述:

-
题目思路:
这道题目本质上讲就是列出图的连通集,但是这个连通集的起点是有约束的:詹姆斯邦德必须第一跳能跳到的点才是连通集的起点。解决这道问题可以使用DFS。
- C语言实现:
错误代码如下:
//孤岛应该被作为单独一个节点来测试
//孤岛周围可能有很多鳄鱼,程序就是要考察这些鳄鱼(节点)的连通集
//里有没有可以跳到岸上的。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdbool.h>
#define MaxPointer 100
struct Pointer
{
int x;
int y;
};
struct Pointer Graph[MaxPointer];
bool Visited[MaxPointer]; //存储点是否被踩过
int jumpmaximum = 0; //007可以跳的最远距离
int pointernum = 0;
//作用:判断从中心可以调到那个鳄鱼头上
bool FirstJump(int i)
{
int dis = 0;
dis = (Graph[i].x - 0) * (Graph[i].x - 0) + (Graph[i].y - 0) * (Graph[i].y - 0);
return ((jumpmaximum + 7.5) * (jumpmaximum + 7.5) >= dis ? true : false);
}
//作用:判断从当前点能否跳到岸上去
//返回值: true 能
// false 不能
bool IsSafe(int i)
{
if (Graph[i].x + jumpmaximum >= 50 || Graph[i].x - jumpmaximum <= -50)
{
if (Graph[i].y + jumpmaximum >= 50 || Graph[i].y - jumpmaximum <= -50)
{
return true;
}
}
return false;
}
//作用:判断能否从i点跳到j点
//返回值: true 能
// false 不能
bool Jump(int i,int j)
{
int dis = 0;
dis = (Graph[i].x - Graph[j].x) * (Graph[i].x - Graph[j].x) + (Graph[i].y - Graph[j].y) * (Graph[i].y - Graph[j].y);
return (jumpmaximum * jumpmaximum >= dis ? true : false);
}
bool DFS(int i)
{
bool answer = false;
int j = 0;
//printf("%d.
",i);
Visited[i] = true; //表示i点已经踩过
//能不能从当前点跳到岸上去
if (IsSafe(i))
{
answer = true;
}
for (j = 0; j < pointernum; j++)
{
if (!Visited[j] && Jump(i, j))
{
answer = DFS(j);
Visited[j] = false;
if (answer == true)
{
break;
}
}
}
return answer;
}
void Save007()
{
bool answer = false;
for (int i = 0;i < pointernum;i++)
{
if (!Visited[i] && FirstJump(i))
{
answer = DFS(i);
if (answer)
{
break;
}
}
}
if (answer)
{
printf("Yes");
}
else
{
printf("No");
}
}
int main()
{
scanf("%d", &pointernum);
scanf("%d", &jumpmaximum);
//初始化所有顶点状态都是未访问过状态
for (int i = 0; i < pointernum; i++)
{
Visited[i] = false;
}
for (int i = 0;i < pointernum;i++)
{
scanf("%d %d",&Graph[i].x,&Graph[i].y);
}
if (jumpmaximum >= 42.5)
{
printf("Yes");
}
Save007();
system("pause");
return 0;
}
最终修改BUG后的版本:
//孤岛应该被作为单独一个节点来测试
//孤岛周围可能有很多鳄鱼,程序就是要考察这些鳄鱼(节点)的连通集
//里有没有可以跳到岸上的。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdbool.h>
#define MaxPointer 100
struct Pointer
{
int x;
int y;
};
struct Pointer Graph[MaxPointer];
bool Visited[MaxPointer]; //存储点是否被踩过
int jumpmaximum = 0; //007可以跳的最远距离
int pointernum = 0;
//作用:判断从中心可以调到那个鳄鱼头上
bool FirstJump(int i)
{
//int dis = 0;
//dis = (Graph[i].x - 0) * (Graph[i].x - 0) + (Graph[i].y - 0) * (Graph[i].y - 0);
//return ((jumpmaximum + 7.5) * (jumpmaximum + 7.5) >= dis ? true : false);
int p1 = pow(Graph[i].x, 2);
int p2 = pow(Graph[i].y, 2);
int r = (jumpmaximum + 7.5) * (jumpmaximum + 7.5);
if (p1 + p2 <= r) {
return true;
}
return false;
}
//作用:判断从当前点能否跳到岸上去
//返回值: true 能
// false 不能
bool IsSafe(int i)
{
if (Graph[i].x + jumpmaximum >= 50 || Graph[i].x - jumpmaximum <= -50
|| Graph[i].y + jumpmaximum >= 50 || Graph[i].y - jumpmaximum <= -50)
{
return true;
}
return false;
}
//作用:判断能否从i点跳到j点
//返回值: true 能
// false 不能
bool Jump(int i,int j)
{
int dis = 0;
dis = (Graph[i].x - Graph[j].x) * (Graph[i].x - Graph[j].x) + (Graph[i].y - Graph[j].y) * (Graph[i].y - Graph[j].y);
return (jumpmaximum * jumpmaximum >= dis ? true : false);
}
bool DFS(int i)
{
bool answer = false;
int j = 0;
//printf("%d.
",i);
Visited[i] = true; //表示i点已经踩过
//能不能从当前点跳到岸上去
if (IsSafe(i))
{
answer = true;
}
for (j = 0; j < pointernum; j++)
{
if (!Visited[j] && Jump(i, j))
{
answer = DFS(j);
Visited[j] = false;
if (answer == true)
{
break;
}
}
}
return answer;
}
void Save007()
{
bool answer = false;
for (int i = 0;i < pointernum;i++)
{
if (!Visited[i] && FirstJump(i))
{
answer = DFS(i);
if (answer)
{
break;
}
}
}
if (answer)
{
printf("Yes");
}
else
{
printf("No");
}
}
int main()
{
scanf("%d", &pointernum);
scanf("%d", &jumpmaximum);
//初始化所有顶点状态都是未访问过状态
for (int i = 0; i < pointernum; i++)
{
Visited[i] = false;
}
for (int i = 0;i < pointernum;i++)
{
scanf("%d %d",&Graph[i].x,&Graph[i].y);
}
if (jumpmaximum >= 42.5)
{
printf("Yes");
}
Save007();
//system("pause");
return 0;
}
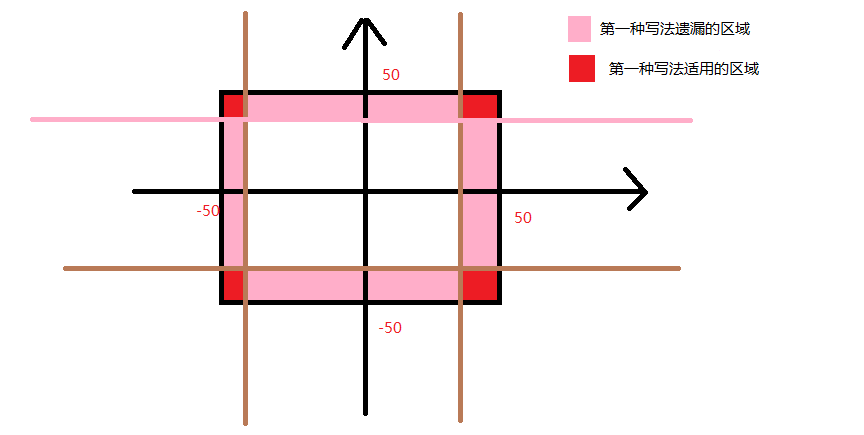
这两个程序主要的差别在最后判断邦德能不能直接从鳄鱼头跳到岸上去,第一个有BUG的版本中,这个判断函数是这样写的:
//作用:判断从当前点能否跳到岸上去
//返回值: true 能
// false 不能
bool IsSafe(int i)
{
if (Graph[i].x + jumpmaximum >= 50 || Graph[i].x - jumpmaximum <= -50)
{
if (Graph[i].y + jumpmaximum >= 50 || Graph[i].y - jumpmaximum <= -50)
{
return true;
}
}
return false;
}
第二个版本中,对这个函数进行了修改:
//作用:判断从当前点能否跳到岸上去
//返回值: true 能
// false 不能
bool IsSafe(int i)
{
if (Graph[i].x + jumpmaximum >= 50 || Graph[i].x - jumpmaximum <= -50
|| Graph[i].y + jumpmaximum >= 50 || Graph[i].y - jumpmaximum <= -50)
{
return true;
}
return false;
}
这两个版本的函数实现区别可以看下面的图,第一个版本的函数遗漏了一些点,所以才导致提交不通过。