题目一览:
1.煤球数目
2.生日蜡烛
3.凑算式
4.快速排序
5.抽签
6.方格填数
7.剪邮票
8.四平方和
9.交换瓶子
10.最大比例
1.煤球数目
有一堆煤球,堆成三角棱锥形。具体:
第一层放1个,
第二层3个(排列成三角形),
第三层6个(排列成三角形),
第四层10个(排列成三角形),
....
如果一共有100层,共有多少个煤球?
请填表示煤球总数目的数字。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
思路:枚举

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int main() { 5 int cnt = 0; 6 int Ans = 0; 7 for(int i=1; i<=100; ++i) { // 枚举层数 8 cnt += i; // 每一层比上一层多i个 9 Ans += cnt; // 计算每一层 10 } 11 printf("%d ", Ans); 12 return 0; 13 }
答案:171700
2.生日蜡烛
某君从某年开始每年都举办一次生日party,并且每次都要吹熄与年龄相同根数的蜡烛。
现在算起来,他一共吹熄了236根蜡烛。
请问,他从多少岁开始过生日party的?
请填写他开始过生日party的年龄数。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
思路:枚举+判断

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 bool flag = true; 5 int age = 0; 6 7 bool check(int x) { 8 int sum = 0; 9 while(sum < 236) { // 这里是< 10 sum += x; 11 x++; 12 } 13 if(sum == 236) return true; 14 else return false; 15 } 16 17 int main() { 18 while(flag && age<100) { 19 age++; 20 if(check(age)) 21 flag = false; 22 } 23 cout << age << endl; 24 return 0; 25 }
答案:26
3.凑算式
B DEF A + --- + ------- = 10 C GHI
(如果显示有问题,可以参见【图1.jpg】)
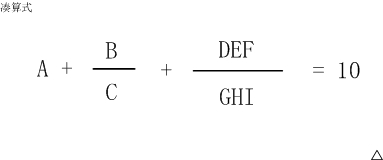
这个算式中A~I代表1~9的数字,不同的字母代表不同的数字。
比如:
6+8/3+952/714 就是一种解法,
5+3/1+972/486 是另一种解法。
这个算式一共有多少种解法?
注意:你提交应该是个整数,不要填写任何多余的内容或说明性文字。
思路:拉成一维数组全排练+判断,值得注意的是B/C和DEF/GHI都是整除。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int a[] = {1, 2, 3, 4, 5, 6, 7, 8, 9}; 5 6 bool check() { 7 int x = a[3]*100 + a[4]*10 + a[5]; 8 int y = a[6]*100 + a[7]*10 + a[8]; 9 if((a[1]*y+a[2]*x)%(a[2]*y) != 0) return false; // 一定要是整除.. 10 // 这里注意两个除法合并到一起 不然单个除不净 11 int t = a[0] + (a[1]*y+a[2]*x)/(a[2]*y); 12 if(t == 10) return true; 13 return false; 14 } 15 16 int main() { 17 int Ans = 0; 18 do { 19 if(check()) Ans++; 20 }while(next_permutation(a, a+9)); 21 printf("%d ", Ans); 22 return 0; 23 } 24 // 29
答案:29
4.快速排序
排序在各种场合经常被用到。
快速排序是十分常用的高效率的算法。
其思想是:先选一个“标尺”,
用它把整个队列过一遍筛子,
以保证:其左边的元素都不大于它,其右边的元素都不小于它。
这样,排序问题就被分割为两个子区间。
再分别对子区间排序就可以了。
下面的代码是一种实现,请分析并填写划线部分缺少的代码。

1 #include <stdio.h> 2 3 void swap(int a[], int i, int j) 4 { 5 int t = a[i]; 6 a[i] = a[j]; 7 a[j] = t; 8 } 9 10 int partition(int a[], int p, int r) 11 { 12 int i = p; 13 int j = r + 1; 14 int x = a[p]; 15 while(1){ 16 while(i<r && a[++i]<x); 17 while(a[--j]>x); 18 if(i>=j) break; 19 swap(a,i,j); 20 } 21 ______________________; // 填空 22 return j; 23 } 24 25 void quicksort(int a[], int p, int r) 26 { 27 if(p<r){ 28 int q = partition(a,p,r); 29 quicksort(a,p,q-1); 30 quicksort(a,q+1,r); 31 } 32 } 33 34 int main() 35 { 36 int i; 37 int a[] = {5,13,6,24,2,8,19,27,6,12,1,17}; 38 int N = 12; 39 40 quicksort(a, 0, N-1); 41 42 for(i=0; i<N; i++) printf("%d ", a[i]); 43 printf(" "); 44 45 return 0; 46 }
注意:只填写缺少的内容,不要书写任何题面已有代码或说明性文字。
思路:我们发现在partition函数中,是以a[p]为标尺,在[p, r]中比a[p]大的和比a[p]小的做交换,那么完成之后就是:a[p],小,小,大,大,大。a[p]显然是要与一个数交换的,那么是i,还是j呢(可以输入i,j输出看一下)。因为我们这个partition函数是要求吧所有小于a[p]的数字放到左边,大于的放到右边,而下标i所指的数是大于a[p]的,与其交换就无法满足要求,所以是与j交换。
答案:
swap(a, p, j);
5.抽签
X星球要派出一个5人组成的观察团前往W星。
其中:
A国最多可以派出4人。
B国最多可以派出2人。
C国最多可以派出2人。
....
那么最终派往W星的观察团会有多少种国别的不同组合呢?
下面的程序解决了这个问题。
数组a[] 中既是每个国家可以派出的最多的名额。
程序执行结果为:
DEFFF
CEFFF
CDFFF
CDEFF
CCFFF
CCEFF
CCDFF
CCDEF
BEFFF
BDFFF
BDEFF
BCFFF
BCEFF
BCDFF
BCDEF
....
(以下省略,总共101行)
1 #include <stdio.h> 2 #define N 6 3 #define M 5 4 #define BUF 1024 5 6 void f(int a[], int k, int m, char b[]) 7 { 8 int i,j; 9 10 if(k==N){ 11 b[M] = 0; 12 if(m==0) printf("%s ",b); 13 return; 14 } 15 16 for(i=0; i<=a[k]; i++){ 17 for(j=0; j<i; j++) b[M-m+j] = k+'A'; 18 ____________; //填空位置 19 } 20 } 21 int main() 22 { 23 int a[N] = {4,2,2,1,1,3}; 24 char b[BUF]; 25 f(a,0,M,b); 26 return 0; 27 }
仔细阅读代码,填写划线部分缺少的内容。
注意:不要填写任何已有内容或说明性文字。
思路:显然第18行我们要调用f函数,首先肯定是(a, , , b),两个数组嘛,然后第10行k==N,说明k是填到第k个,那么就变成了(a, k+1, , b),第12行判断m==0,说明这第三个参数可能输m-1,但测试一下发现并不是,那就只能是m-i了,测试发现正确。
答案:
f(a, k+1, m-i, b)
6.方格填数
如下的10个格子
+--+--+--+
| | | |
+--+--+--+--+
| | | | |
+--+--+--+--+
| | | |
+--+--+--+

(如果显示有问题,也可以参看【图1.jpg】)
填入0~9的数字。要求:连续的两个数字不能相邻。
(左右、上下、对角都算相邻)
一共有多少种可能的填数方案?
请填写表示方案数目的整数。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
方法一:将该10个格子按顺序拉成一个一维数组,然后将十个数字填进去(全排列),填完之后进行判断即可。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int a[11], Ans; 5 6 int calc(int x, int y) { 7 return abs(a[x]-a[y]); 8 } 9 10 bool check() { 11 if(calc(0, 1) == 1) return false; 12 if(calc(0, 3) == 1) return false; 13 if(calc(0, 4) == 1) return false; 14 if(calc(0, 5) == 1) return false; 15 16 if(calc(1, 2) == 1) return false; 17 if(calc(1, 4) == 1) return false; 18 if(calc(1, 5) == 1) return false; 19 if(calc(1, 6) == 1) return false; 20 21 if(calc(2, 5) == 1) return false; 22 if(calc(2, 6) == 1) return false; 23 24 if(calc(3, 4) == 1) return false; 25 if(calc(3, 7) == 1) return false; 26 if(calc(3, 8) == 1) return false; 27 28 if(calc(4, 5) == 1) return false; 29 if(calc(4, 7) == 1) return false; 30 if(calc(4, 8) == 1) return false; 31 if(calc(4, 9) == 1) return false; 32 33 if(calc(5, 6) == 1) return false; 34 if(calc(5, 8) == 1) return false; 35 if(calc(5, 9) == 1) return false; 36 37 if(calc(6, 9) == 1) return false; 38 if(calc(7, 8) == 1) return false; 39 if(calc(8, 9) == 1) return false; 40 return true; 41 } 42 43 void dfs(int pos) { 44 if(pos == 10) { 45 if(check()) Ans ++; 46 return ; 47 } 48 for(int i=pos; i<10; ++i) { 49 int t = a[pos]; a[pos] = a[i]; a[i] = t; 50 dfs(pos+1); 51 t = a[pos]; a[pos] = a[i]; a[i] = t; 52 } 53 } 54 55 int main() { 56 for(int i=0; i<=10; ++i) 57 a[i] = i; 58 dfs(0); 59 printf("%d ", Ans); 60 return 0; 61 }
方法二:在原图的基础上加一圈,然后判断。这个方法的check函数较为简洁。初始化可以不是-10,只要不与0-9相差±1即可。如图:
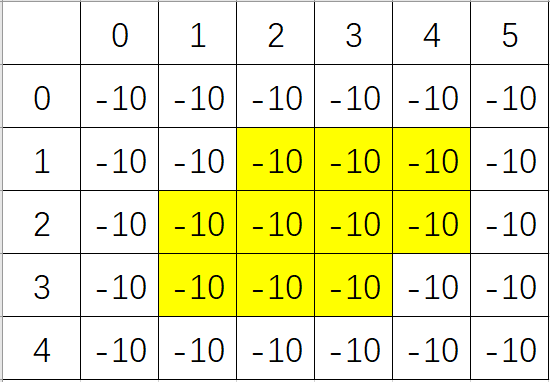

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int Map[5][6], Ans; 5 bool vis[10]; 6 7 bool check(int x, int y) { 8 for(int i=x-1; i<=x+1; ++i) { 9 for(int j=y-1; j<=y+1; ++j) { 10 if(abs(Map[x][y]-Map[i][j]) == 1) 11 return false; 12 } 13 } 14 return true; 15 } 16 17 void dfs(int x, int y) { 18 if(x==3 && y==4) { 19 Ans++; 20 return ; 21 } 22 for(int i=0; i<10; ++i) { 23 if(vis[i]) continue; //这个数字用了 24 Map[x][y] = i; // 先放着 25 if(!check(x, y)) { 26 Map[x][y] = -10; // 27 continue; //放下不符规则 28 } 29 vis[i] = true; 30 if(y == 4) 31 dfs(x+1, 1); // 换行 32 else dfs(x, y+1); // 右边的格子 33 Map[x][y] = -10; // 回溯 34 vis[i] = false; 35 } 36 } 37 38 int main() { 39 for(int i=0; i<10; ++i) vis[i] = false; 40 for(int i=0; i<5; ++i) // 外面加一圈 41 for(int j=0; j<6; ++j) 42 Map[i][j] = -10; 43 dfs(1, 2); //第一个填数的格子是(1,2) 44 printf("%d ", Ans); 45 return 0; 46 }
答案:1580
7.剪邮票
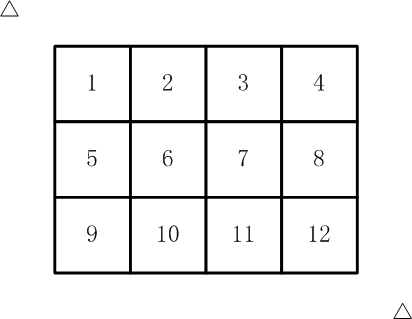
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来,要求必须是连着的。
(仅仅连接一个角不算相连)
比如,【图2.jpg】,【图3.jpg】中,粉红色所示部分就是合格的剪取。
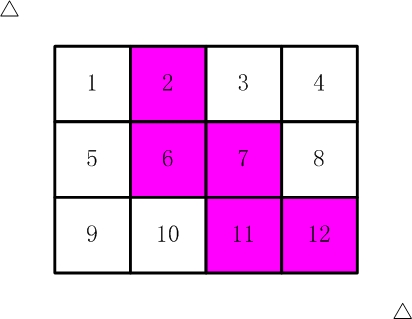
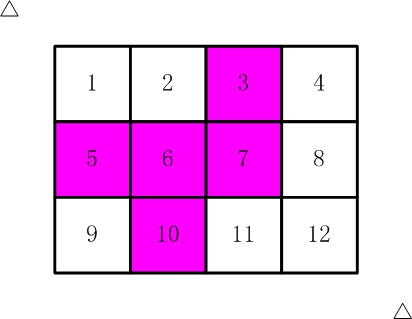
请你计算,一共有多少种不同的剪取方法。
请填写表示方案数目的整数。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
思路:直接搜索是不大可能的,我们可以把它转变成全排列问题。因为一共12张,需要5张,我们可以创建一个数组,存放5个1和7个0,然后对其进行全排列(这里值得注意的是普通的全排列对重复的数字会产生重复的全排列,简单起见,我们使用c++里面STL中的next_permutation()),然后将其转化成二维数组,然后用dfs搜索看看有几个连通块,只有一个连通块就是一个可行的方案。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int n = 3, m = 4, Map[3][4], Ans; 5 int a[] = {0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1}; 6 int u[4] = {-1, 0, 0, 1}, 7 v[4] = {0, -1, 1, 0}; 8 9 void dfs(int x, int y) { 10 Map[x][y] = 0; 11 for(int i=0; i<4; ++i) { 12 int xx = x + u[i]; 13 int yy = y + v[i]; 14 if(xx>=0 && xx<3 && yy>=0 && yy<4 && Map[xx][yy]==1) 15 dfs(xx, yy); 16 } 17 } 18 19 bool check() { 20 for(int i=0; i<3; ++i) 21 for(int j=0; j<4; ++j) 22 Map[i][j] = a[4*i+j]; 23 int cnt = 0; 24 for(int i=0; i<3; ++i) 25 for(int j=0; j<4; ++j) { 26 if(Map[i][j] == 1) { 27 dfs(i, j); 28 cnt++; 29 } 30 } 31 if(cnt == 1) return true; 32 return false; 33 } 34 35 void work() { // 利用next_permutation生成不重复的排列 36 do { 37 if(check()) Ans++; 38 }while(next_permutation(a, a+12)); 39 } 40 41 int main() { 42 43 work(); 44 printf("%d ", Ans); 45 46 return 0; 47 }
答案:116
8.四平方和
四平方和定理,又称为拉格朗日定理:
每个正整数都可以表示为至多4个正整数的平方和。
如果把0包括进去,就正好可以表示为4个数的平方和。
比如:
5 = 0^2 + 0^2 + 1^2 + 2^2
7 = 1^2 + 1^2 + 1^2 + 2^2
(^符号表示乘方的意思)
对于一个给定的正整数,可能存在多种平方和的表示法。
要求你对4个数排序:
0 <= a <= b <= c <= d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列,最后输出第一个表示法
程序输入为一个正整数N (N<5000000)
要求输出4个非负整数,按从小到大排序,中间用空格分开
例如,输入:
5
则程序应该输出:
0 0 1 2
再例如,输入:
12
则程序应该输出:
0 2 2 2
再例如,输入:
773535
则程序应该输出:
1 1 267 838
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
方法一:由题可知a*a<=N/4,b*b<=N/3,c*c<=N/2,d*d<=N,那么我们就可以四层循环来做,但一个很明显的问题就是会T。然后就是各种神奇的优化,比如说让a*a<=50,b*b<=500。。。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int N; 5 6 int main() { 7 cin >> N; 8 for(int a=0; a*a<=50; a++) { 9 for(int b=a; b*b<=500; b++) { 10 if(b*b > N) break; 11 for(int c=b; c*c<=N/2; c++) { 12 if(c*c > N) break; 13 for(int d=c; d*d<=N; d++) { 14 if(d*d > N) break; 15 if(a*a+b*b+c*c+d*d == N) { 16 printf("%d %d %d %d ", a, b, c, d); 17 return 0; 18 } 19 } 20 } 21 } 22 } 23 return 0; 24 }
方法二:我们可以事先处理c*c+d*d,把结果存起来,用map把结果与c或者d形成映射。然后再枚举a、b,用N-a*a-b*b来得到c*c+d*d,判断预处理里面有没有,有的话在N-a*a-b*b-c*c开方求出d即可。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 map<int, int> Map; 5 int N; 6 7 int main() { 8 scanf("%d", &N); 9 for(int c=0; c*c<=N/2; ++c) 10 for(int d=c; c*c+d*d<=N; ++d) 11 if(Map.find(c*c+d*d) == Map.end()) 12 Map[c*c+d*d] = c; 13 for(int a=0; a*a<=N/4; ++a) { 14 for(int b=a; a*a+b*b<=N/2; ++b) { 15 if(Map.find(N-a*a-b*b) != Map.end()) { 16 int c = Map[N-a*a-b*b]; 17 int d = (int)sqrt(N-a*a-b*b-c*c); 18 printf("%d %d %d %d ", a, b, c, d); 19 return 0; 20 } 21 } 22 } 23 return 0; 24 }
9.交换瓶子
有N个瓶子,编号 1 ~ N,放在架子上。
比如有5个瓶子:
2 1 3 5 4
要求每次拿起2个瓶子,交换它们的位置。
经过若干次后,使得瓶子的序号为:
1 2 3 4 5
对于这么简单的情况,显然,至少需要交换2次就可以复位。
如果瓶子更多呢?你可以通过编程来解决。
输入格式为两行:
第一行: 一个正整数N(N<10000), 表示瓶子的数目
第二行:N个正整数,用空格分开,表示瓶子目前的排列情况。
输出数据为一行一个正整数,表示至少交换多少次,才能完成排序。
例如,输入:
5
3 1 2 5 4
程序应该输出:
3
再例如,输入:
5
5 4 3 2 1
程序应该输出:
2
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
思路:从左到右扫一遍,碰到一个数在不是他的位置上,就找到它应该所在的位置(无论该位置上是谁),与其进行交换,然后答案加一。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int N, a[10101], Ans; 5 6 int get_pos(int x) { 7 for(int i=1; i<=N; ++i) 8 if(a[i] == x) 9 return i; 10 return -1; 11 } 12 13 int main() { 14 cin >> N; 15 for(int i=1; i<=N; ++i) scanf("%d", &a[i]); 16 for(int i=1; i<=N; ++i) { 17 if(a[i] != i) { 18 int pos = get_pos(i); 19 swap(a[i], a[pos]); 20 Ans ++; 21 } 22 } 23 printf("%d ", Ans); 24 return 0; 25 }
10.最大比例
X星球的某个大奖赛设了M级奖励。每个级别的奖金是一个正整数。
并且,相邻的两个级别间的比例是个固定值。
也就是说:所有级别的奖金数构成了一个等比数列。比如:
16,24,36,54
其等比值为:3/2
现在,我们随机调查了一些获奖者的奖金数。
请你据此推算可能的最大的等比值。
输入格式:
第一行为数字 N (0<N<100),表示接下的一行包含N个正整数
第二行N个正整数Xi(Xi<1 000 000 000 000),用空格分开。每个整数表示调查到的某人的奖金数额
要求输出:
一个形如A/B的分数,要求A、B互质。表示可能的最大比例系数
测试数据保证了输入格式正确,并且最大比例是存在的。
例如,输入:
3
1250 200 32
程序应该输出:
25/4
再例如,输入:
4
3125 32 32 200
程序应该输出:
5/2
再例如,输入:
3
549755813888 524288 2
程序应该输出:
4/1
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
