题目描述
kkk制造了一个序列,这个序列里的数全是由正整数构成的。你别认为她的数列很神奇——其实就是1, 2, …, n而已。当然,n是给定的。kkk的同学lzn认为0是一个好数字(看上去很饱满有木有),所以他机智的趁kkk不在把这个序列全变成了0(其实只是准备窝)~
可是kkk突然回来了!于是lzn的计划破灭了。但是他并不甘心,就和kkk说:我可以每次从这个序列中选取一些数,然后一起减去一个相同的数(当然也是正整数)。然后经过有(wu)限(qiong)次这样的操作后,这个序列就可以全变成0。
kkk当然不信咯,于是lzn就求出了他最少要做几次这样的操作,才能使这个序列全部变成0。
输入输出格式
输入格式:
一个正整数n
输出格式:
最少操作次数
如果无解输出-1
输入输出样例
说明
1<=n<=10^9
2333
大水题啊,今晚上一遍就过了哈哈哈哈!
找规律找规律。

然后,发现
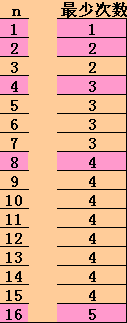
次数1,2,3,4,5的第一组对应的n,
分别是2^0,2^1,2^2,2^3,2^4.
so,规律出来了:
如果log2(n)是整数的话,那么答案就是log2(n)+1;
如果不是整数,那么答案就是log2(n)向上取整的那个数再+1.
2333我真的是太聪明了!
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 using namespace std; 7 8 long long n; 9 10 int main() 11 { 12 scanf("%lld",&n); 13 int x=log2(n); 14 if(x-(int)x==0) 15 { 16 printf("%d",x+1); 17 return 0; 18 } 19 else 20 { 21 printf("%d",ceil(x)+1); 22 return 0; 23 } 24 }
此题跟-1没啥关系。