图论学习五之minimal spanning tree最小生成树

　　　　　　生成树的概念

 生成树
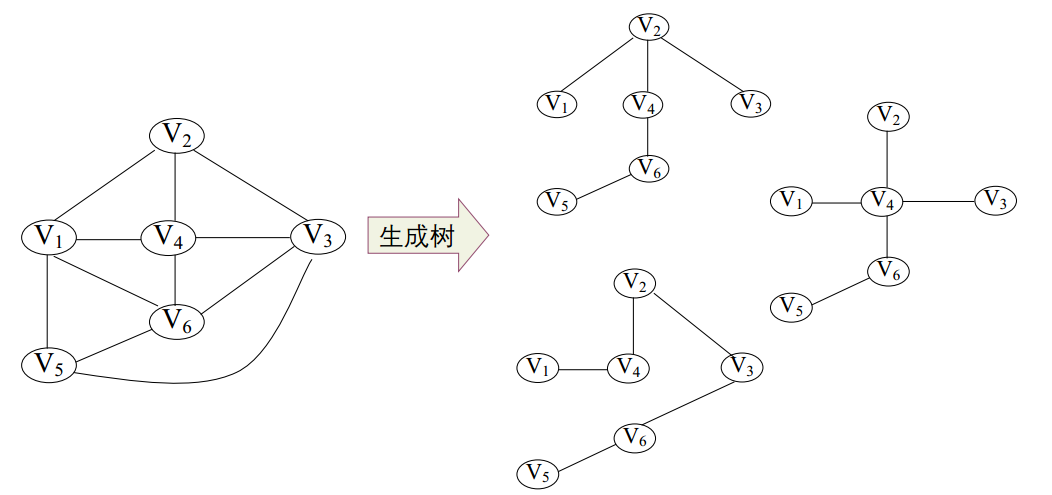
　　 一个连通图的生成树是一个极小连通子图，它含有图中全
   　　 部顶点，但只有足以构成一棵树的n-1条边。
　　 生成树不唯一

　　　　　　最小生成树

生成树的代价等于其边上的权值之和。

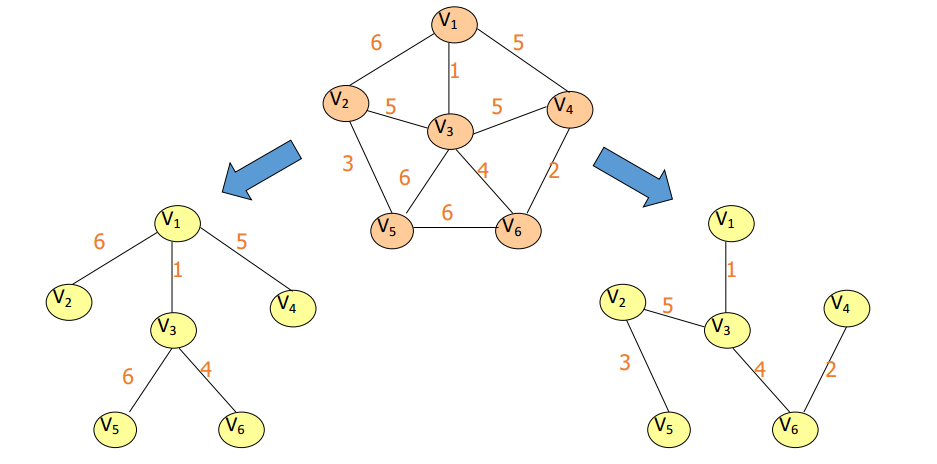
　　　　　　 两种常用的构造最小生成树的方法：

 Prim 算法
 Kruskal 算法（重要）

　　　　　　Prim算法

假设N=(V， E)是连通网， TE是N上最小生成树中边的集合。
算法从U={u0}(u0∈V)， TE={}开始，重复执行下述操作：
　　　在所有u∈U， v∈V-U的边(u， v)中找一条代价最小的边(u0 ,v0),将
　　      其并入集合TE，同时将v0并入U集合。
　　   当U=V则结束，此时TE中必有n-1条边，则T=(V， {TE})为N的最小生
　　      成树。
prim算法构造最小生成树的过程是从一个顶点U={u0}作初态，
不断寻找与U中顶点相邻且代价最小的边的另一个顶点，扩
充到U集合直至U=V为止。

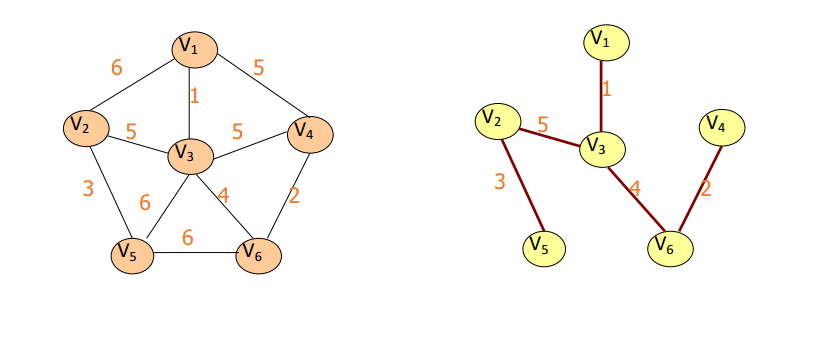
 prim算法求最小生成树：从生
成树中只有一个顶点开始，到
顶点全部进入生成树为止

 

　　　　　　Kruskal算法

假设连通网N=(V， E)，则令最小生成树的初始状态
  为只有n个顶点而无边的非连通图T=(V， {})，图中
  每个顶点自成一个连通分量。

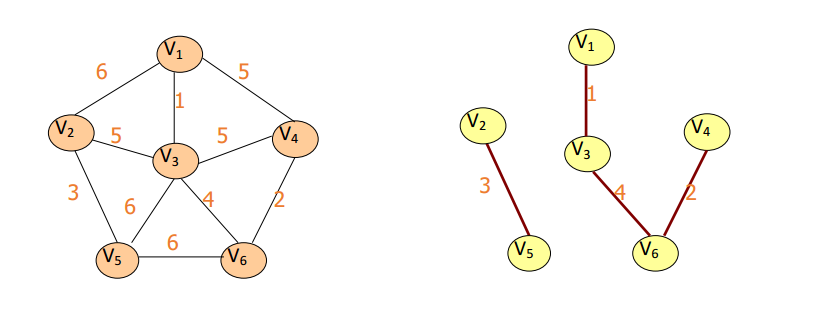
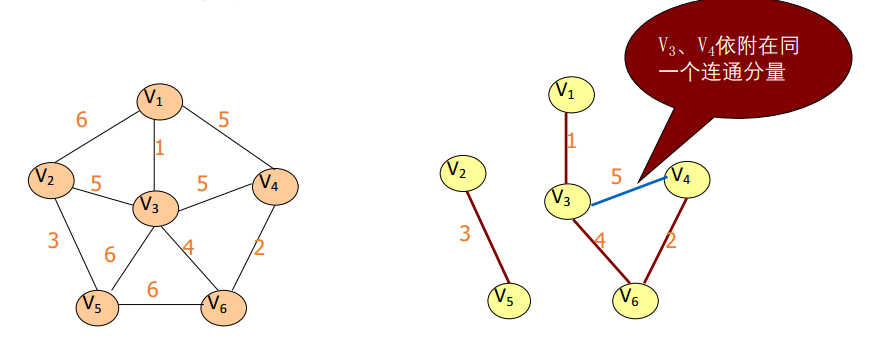
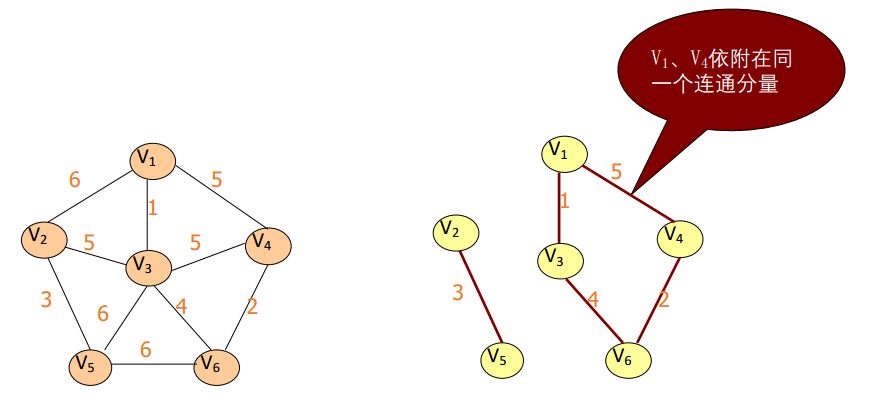
在E中选择代价最小的边，若该边依附的顶点落在T
  中不同的连通分量上，则将此边加入到T中，否则
  舍去此边而选择下一条代价最小的边。依次类推，
  直至T中所有顶点都在同一连通分量上为止。

 

克鲁斯卡尔算法求最小生成树

 

---

如果你不开心，那我就把右边这个帅傻子分享给你吧，
你看，他这么好看，跟个zz一样看着你，你还伤心吗？
真的！这照片盯上他五秒钟就想笑了。
一切都会过去的。
时间时间会给你答案2333