教程:RICE大学在edx上的相关课程“ELEC301x Discrete Time Signals and Systems
1. 离散时间信号与系统
信号是可以探测到的物理量,并且其中携带了信息。
Signal (n): A detectable physical quantity ...by which messages or information can be transmitted (Merriam-Webster)

信号处理系统是对信号中携带的信息进行处理。例如滤波,编码,通信...

信号是函数,其中自变量是独立的变量,而因变量之间往往是相关的。在信号x[n]中,每个独立变量n产生一个值x[n],而x[n]之间是不独立的(例如语音,同一段话的语音的波形是相似的)。离散时间信号中的n是整数(大多数情况是时间),而x[n]一般是实数或者复数。

在刻画信号时使用离散的点,横轴是离散的,纵轴是实数。现实中的信号看上去更加复杂一点,但本质相同。
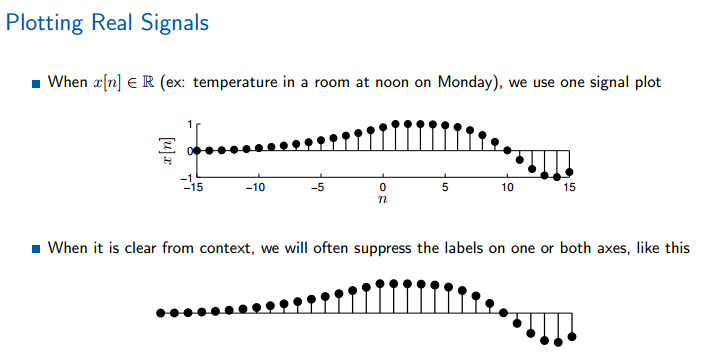
 o
o
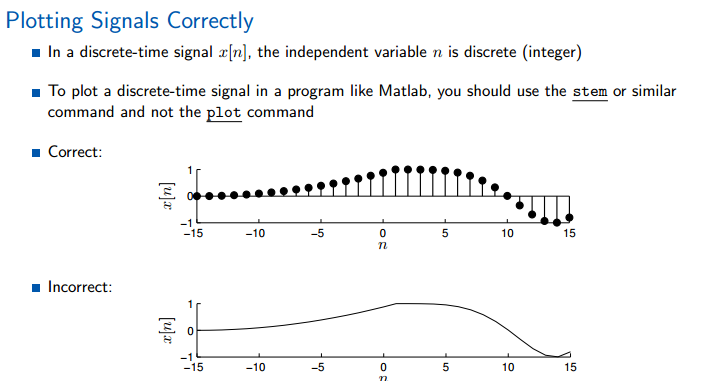
在matlab中使用stem命令,而不是plot,plot画的是连续的图。
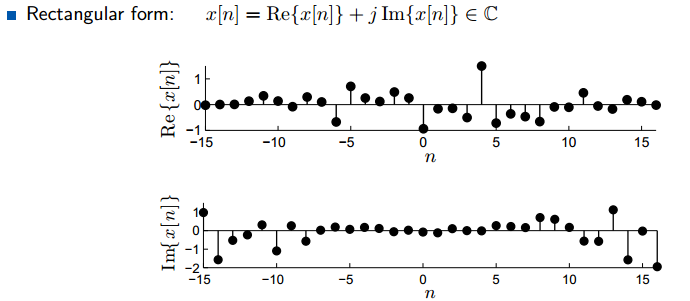
复数信号的写法有两种:极坐标和直角坐标。 工程上用j表示复数轴,而数学中用i表示复数。复数信号的表示中,实数常常表示

直角坐标系中,信号拆分成两部分。
在极坐标表示中,复数信号也拆分成幅值和角度。
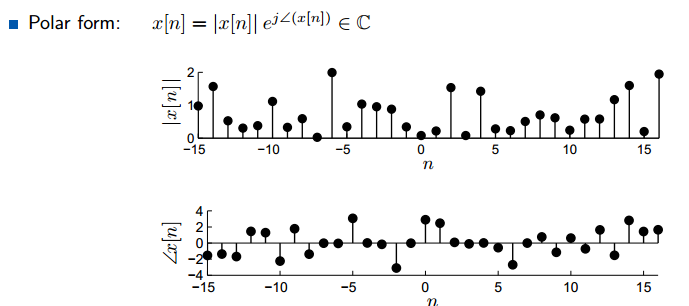
总结:信号中的独立变量n是整数,表示时间;信号中的非独立变量x[n]是实数或复数。

2.信号的性质
学习内容:有限、无限信号;周期信号;因果信号;奇、偶信号;数字信号
有限、无限信号表示的是信号的长度n的范围。

注意:有限信号指的是在信号两端没有定义,不是0也不是别的,而是没定义。
周期信号,非周期信号叫做aperiodic。
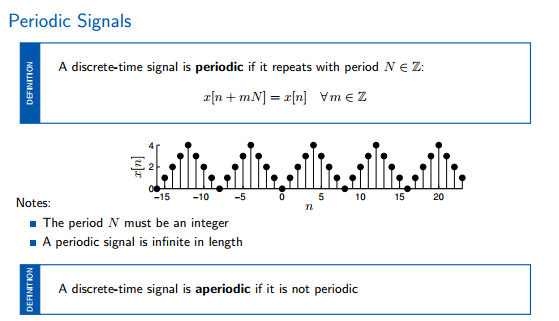
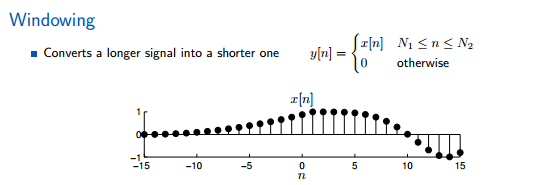
有限信号与无限信号之间的转换:通过在无限信号中的某段上加窗口将无限信号转化为有限信号.将有限信号进行0填充或者周期化变为无限信号。


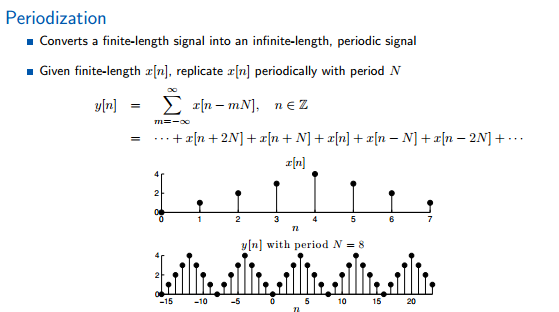
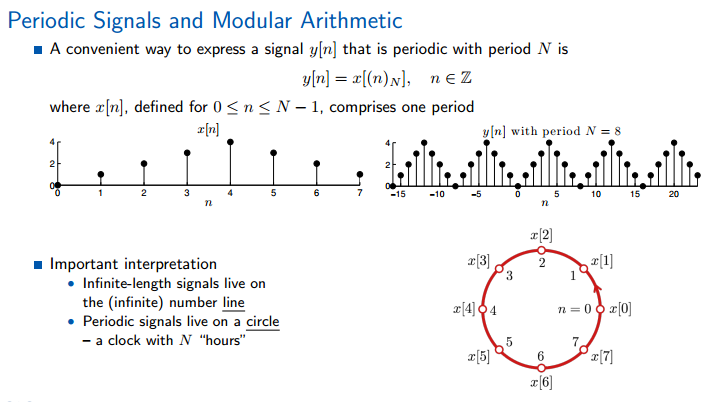
周期化,就是将信号按照周期N进行连续的平移,是信号在整个轴上补充完整。
模运算与周期信号息息相关。进行N的模运算就像使用一个含有N个小时的手表。
例如画一个以含有8小时的表。那么4 mod 8的结果就是从0开始转4下,结果为4;12 mod 8的结果就是从0开始转12下,结果还是4(转了完整的一周又走到4)。-4 mod 8的结果是负方向转4下,以此类推可以得到任意数mod8的结果。模运算与生俱来就是周期性的。

2.5.通过模运算对信号进行周期化。
一个长度为N的信号x[n],通过模运算可以十分方便的表示该信号的周期化。
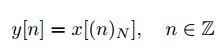
下面的左图为有限信号,右图为该信号的周期化(无限信号)。无限信号的时间轴是无限长的直线,周期信号是一个含有N(周期长度)的圆环。

有限信号和周期信号含有的信息是相同的。
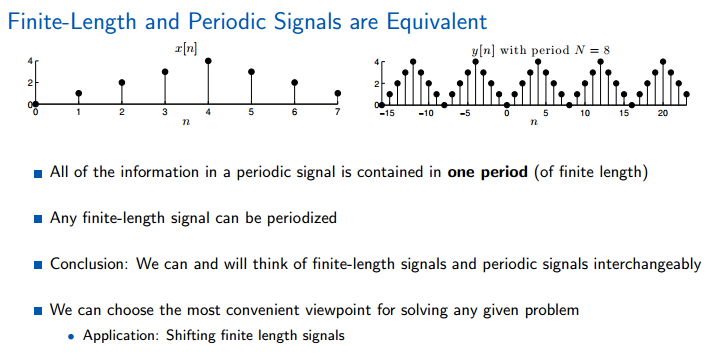
因果信号(Causal Signals):信号中n小于0时的信号值为0。

基数、偶数信号与奇函数偶函数定义相同。

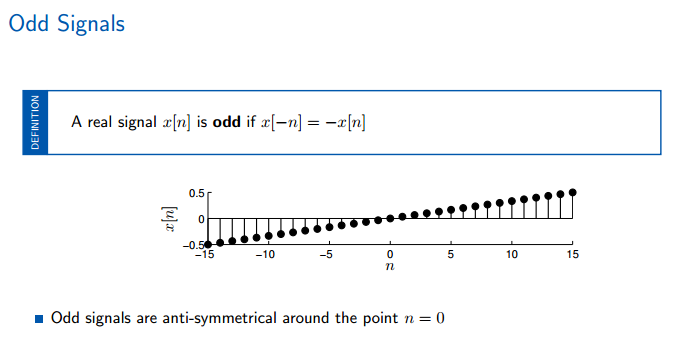
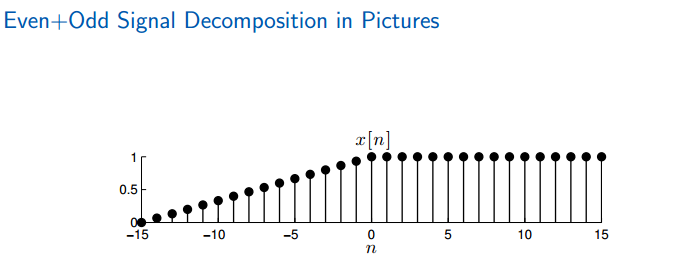
任何信号都可以由奇信号和偶信号共同组成。

奇数和偶数信号部分,从组成上看,偶数部分抵消了奇数的信号,而基数信号抵消了偶数的信号,所以每个信号都是只含有奇数和偶数的。

数字信号时离散时域信号的子集。数字信号的特点是bit与信号值联系到了一起,这个是数字系统的基础啊。

总结:
信号可以使用不同方法归类:实数,复数,有限,无限,周期,非周期,因果,非因果,奇数,偶数...。有限信号和周期信号涵盖的信息相等;模运算非常有用。

3.信号移位
原则是左加右减, 移位指的的是信号值x[n]位置的平行移动。
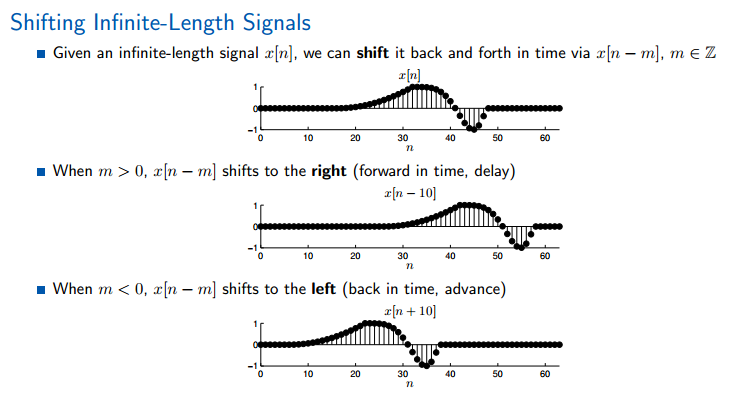
仍然是左加右减,圆环的正向为左。注意周期信号的表达方式。
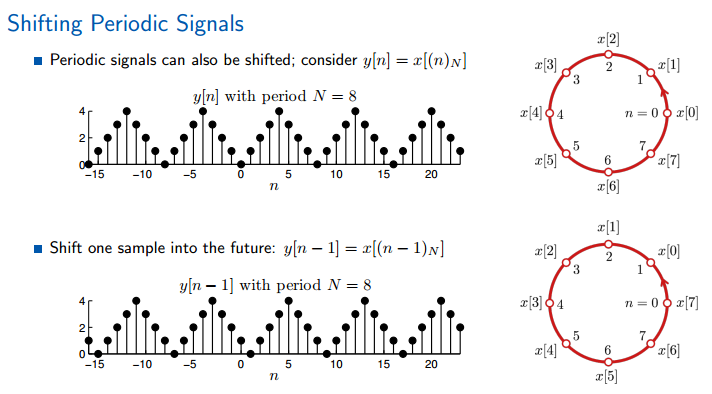
有限信号在移位的时候,出现定义域和值域不存在的问题,解决办法就是进行循环移位(跟周期信号很像)。

就是将有限信号首位相连,构成一个圆环,这样无路如何移位,都没有问题。



总结:
信号的移位是指在时间轴上将信号进行移动。模运算提供了一个简单的进行周期信号移位的方式。

4. Test signals
需要了解:Delta function,Unit step,Real exponetial,sinusoids,complex exponentials。这些信号作为无限信号进行介绍,但是每个信号也有一个有限长度的信号与其相等。
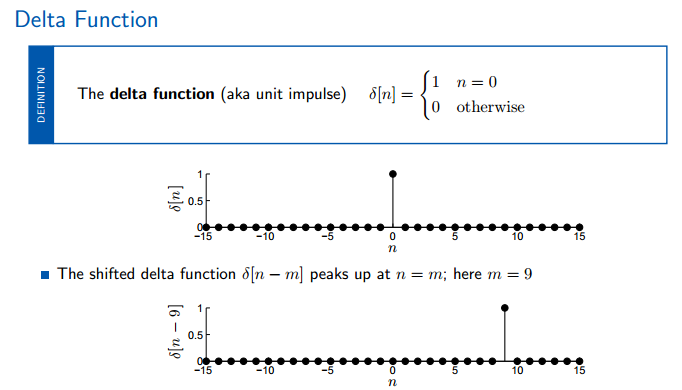
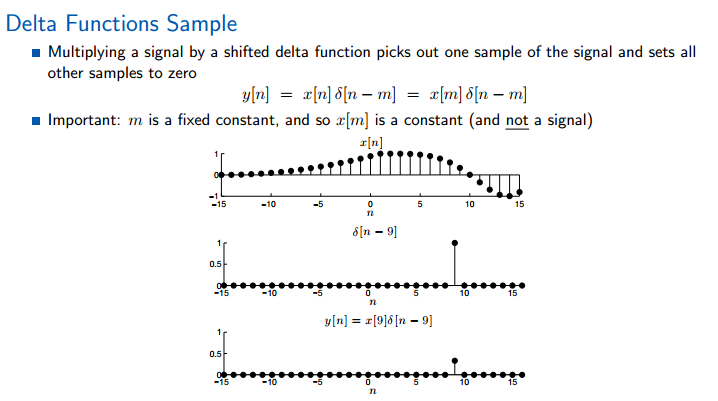
此处需要注意,m是个常数。x[n]delta[n-m]代表两个信号相乘,而x[m]delta[n-m]代表一个信号与一个数相乘。


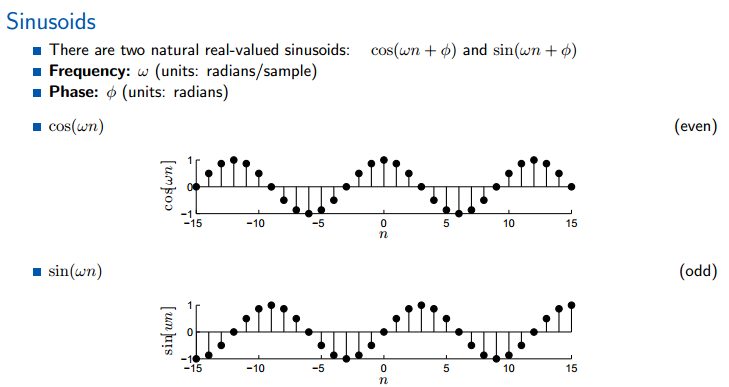
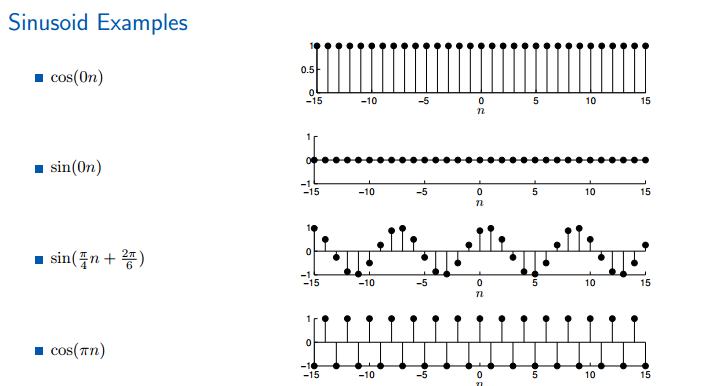
5.正弦函数
正弦函数(包括我们常说的正弦,余弦)出现在无数的学科当中,特别是信号处理;他们是离散傅里叶变换和离散时域傅里叶变换的基础。学习目标:实数正弦函数,复数正弦函数,复数指数函数
由频率omega和相位决定的函数。频率单位是每个样本点转过的弧度,相位的单位就是弧度。余弦函数时偶函数,正弦函数是奇函数,前面我们曾经推出结论,任何信号都可以由偶函数和奇函数组成!!!

复数正弦函数:根据欧拉公式得到复数包含了正弦部分(复数)和余弦部分(实数)。
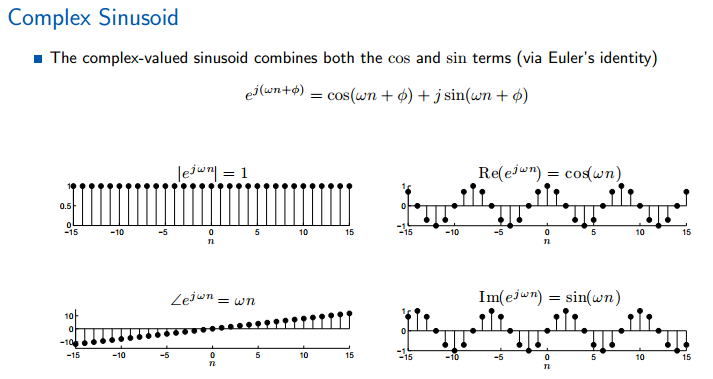
复数正弦是在Z轴上的螺旋线,包含两种变化,频率的正负决定了螺旋线的旋转方向。

复数正弦中的负数频率并不可怕,仅仅是复数轴的sin函数的正负发生了变化,而cos函数完全相同。

相位的变化比较有趣,相位的移动与频率无关,也就是说并不是在频率轴中进行整数移动(每次都移动到整数nw的位置)。而是跟周期2pi有关系,例如pi/4,就是移动1/8个周期,此时采样频率没有变化,所以函数值为1的点(在第一个函数中)采样不到了。

总结:
正弦函数再理论和应用中都很重要,包含频率和相位两个部分。
复数正弦函数是一个三维的螺旋,代表了正弦和余弦。其中频率为负数不用害怕,仅仅是螺旋线反向旋转而已。

6.离散时域正弦线函数非常奇怪
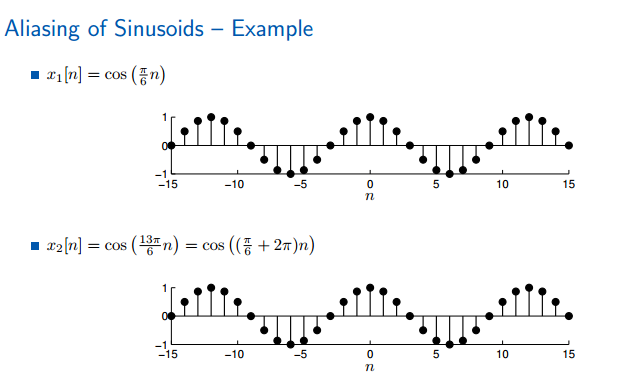
离散时域正弦函数有两个特别奇怪的地方,他们都和频率omega有关系:一个是混叠;另一个是反周期。
两个频率不同的离散时域正弦信号的图像完全相同,这就叫做混叠。

 i
i
只有omega在2pi之内,才不会出现混叠。一般使用两个定义域:[0,2pi],[-pi,pi]

谐波正弦信号。

实验:
随着k的增加,角频率w不断增加,但是我们发现信号并不是随着角频率的增加而频率变得越来越快。
而k=4时,信号的周期最短,离散正弦信号的频率转换最快。
信号的实数部分:k=1和k=7两个信号一模一样(发生混叠)。
信号的虚数部分:k=1和k=7两个信号是完全相反的关系(相当于sin(-wn)=-sin(wn)),因为k=7时,w=7*pi/4,相当于-1*pi/4, 与k=1相反。

将信号以图像的形式表示出来,这个也叫做DFT DFT DFT.两个特点:
k=1和k=7(等等)时,信号的实数部分完全相同,而虚数部分完全相反。
实数部分和虚数部分都是沿着主对角线对称。
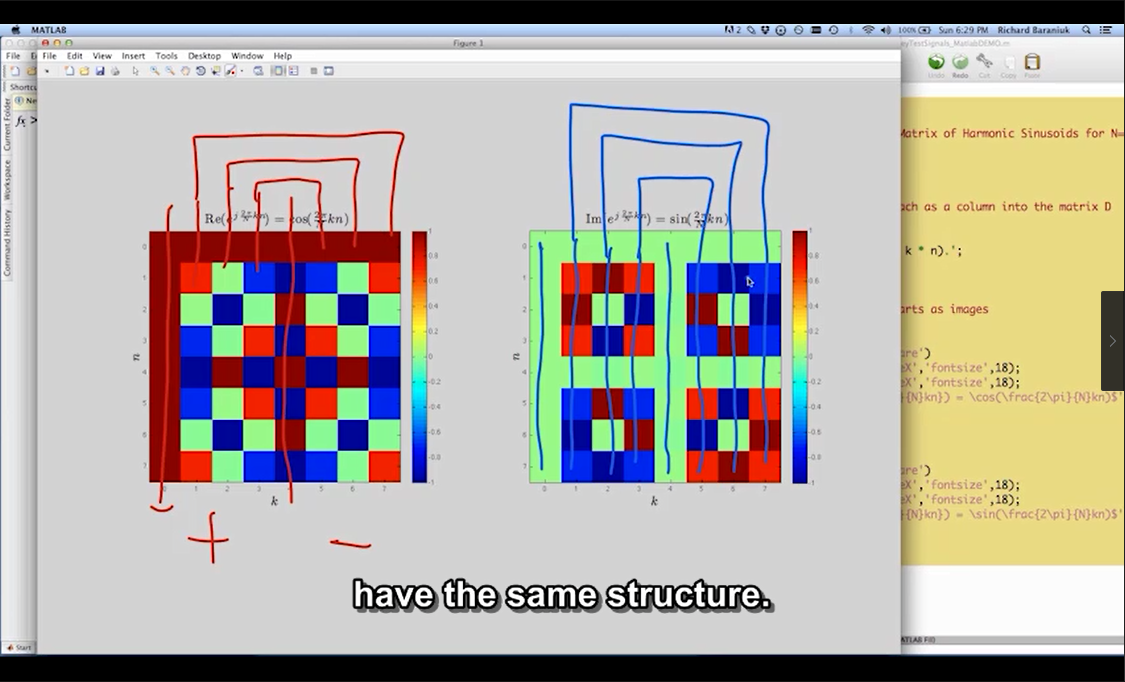
总结:
只有谐波正弦频率的信号才是具有周期的离散正弦信号。
信号长度N决定了k的取值范围,例如N=8决定了0-7的范围,从而确定了DFT的频率个数,同时N也决定了DFT后的信号长度。
最图像上可以看出更明显的区别DFT后的信号有很强的规律。
前面涉及到的复数(离散时域正余弦函数)的复数中,指数部分是个纯虚数,也就是说都是模长为1的复数。
那么,更一般化的复数是什么样子呢?其中,z的模长不仅仅是1.

复指数实际上是一个螺旋,其中omega决定了螺旋旋转的速度,而z决定了螺旋的半径大小。所以,一般情况下就是一个随着时间不断变大或者变小的螺旋。

从平面上看,就是信号的幅值不断变大或者变小的情况。
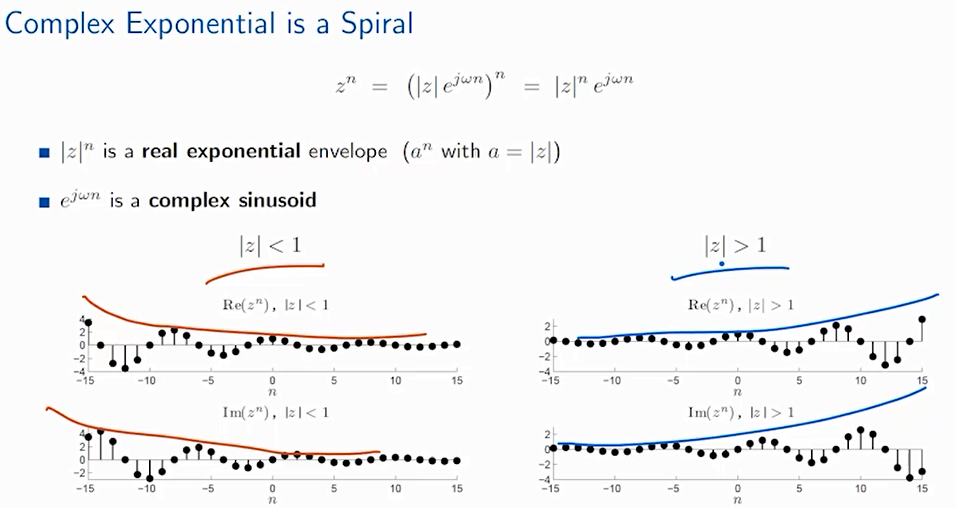
总结:
