7.信号是向量
信号是数学对象,我们将要展示分析信号几何性质的工具-线性代数。通过线性空间的解读,我们可以对信号的强度,信号之间的相似程度进行分析。使用矩阵可以更好地理解信号处理过程。

向量空间的定义,就是一个线性空间的定义。
在实数空间R和复数空间C都有效,常常表述为N维的空间。我们将使用二维空间进行举例。

学习中,仅仅使用x就代表二维空间中的向量,并且每个向量的分量从0开始计数,而不是1.标量alpha是实数。向量空间的性质1:缩放(尺度变换)就是alpha x。

向量空间的性质2:两个向量相加,仍然处于这个向量空间。
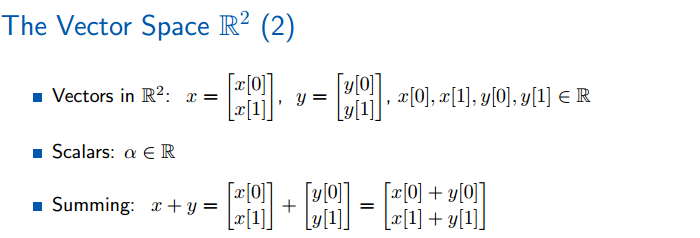
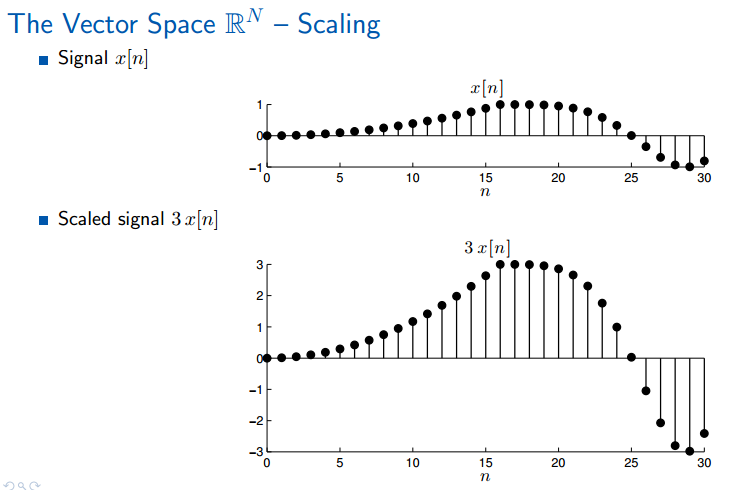
信号的相加,表示两个信号的混合(mix)后的新的信号。

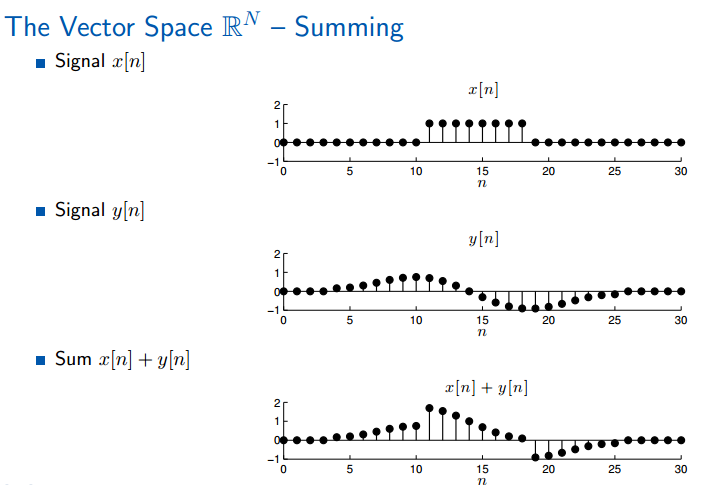
复数向量空间仅在实数向量空间进行简单的修改:信号中的每个分量是一个复数(是复数就存在两种表示方法:复平面坐标与极坐标)。

直角坐标系表示:分成两个向量;极坐标系,注意每个信号的大小是绝对值(其实是该信号在的长度)。
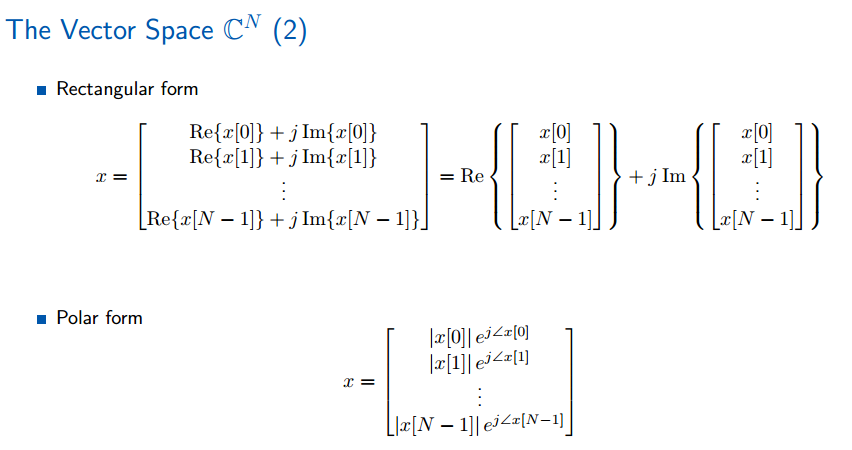

8.信号的线性组合
许多信号处理的基础是多个信号的混合相加,线性组合结果仍然是该向量空间中的向量。

假设每个信号(向量)都是一种乐器产生的时域信号。混音就是简单将他们进行线性组合(混音哦,好帅)

线性组合=矩阵相乘,每个xm都是一个向量(列),代表一种乐器随着时间出现的声音的嘛,而线性组合就是矩阵和向量的乘积。

更加血腥的细节!!! xm的信号长度为N,而一共有M种信号,将其细节进行展示如下。所以信号得到两种表述,矩阵表述(n行m列的矩阵)[X]n,m= xm[n](一共有m种信号,每个信号长度为n)。分别把X视为标量和把x视为向量。

所以信号的线性组合就是矩阵的乘法

总结:
线性代数在数字信号处理中太重要了!!!
信号存在于向量空间的向量!!!
通过线性组合,我们可以将多个信号组合成一个新的信号。
线性组合其实就是矩阵和向量的乘法。

9.信号的范数(Norm)
出现一个问题: 如何衡量信号(向量)的强度?
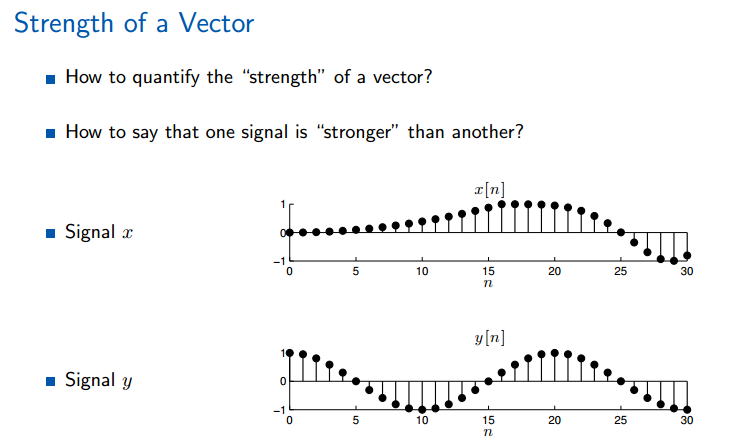
信号的强度通过范数进行描述,其中2范数(也叫欧式距离,欧式距离,欧式距离)定义为一个信号的能量(power)。(注意2范数的写法和它的缩写方法);例子中是复数空间哦。


P范数表示信号的绝对值的p次方的累加,最后再进行p次开方。1范数为每个信号分量的绝对值的和。注意:都是对信号分量绝对值的操作,即表示该信号向量的每个维度上的操作。

有意思的来了!!!无穷范数表示的是一个信号中,幅值最大的分量。
2范式描述的是信号的能量,而无穷范式描述的是信号的峰值(该信号分量的1范式的值,不是欧式距离。注意注意注意,复数空间中这个值是该信号的长度)。

应用举例:扬声器
在磁铁周围缠绕一层线圈(coil of wire),在振动一侧,将线圈与纸质的椎体链接(paper cone),当线圈中流过电流,电磁效应使得线圈沿着轴向左右移动,拉动纸质椎体进行振动,最后发声。
如果能量(2范式)的值太大,线圈就会由于过热而融化。
如果峰值(无穷范式)的值太大,线圈就会左右移动的太厉害,导致纸质椎体脱胶(回忆一下,真的好常见啊。)

例子2:自动驾驶汽车
2范数表示汽车的轨迹相对正确路线的拟合程度。 (能量越小,拟合程度越高,表示汽车沿着真个轨道走的越好)。但是,仅仅损失函数的值达到最好还是不够,如果无穷范数过大,表示某一次的偏离及其严重,那么就会产生严重事故。 所以,这个时候一般需要在轨迹两侧建立警戒线,而该车的轨迹的无穷范数的值不允许超过警戒线范围。

向量的标准化(归一化):将向量的长度化为1.

总结:
范数测量了信号的强度,我们介绍了1范数,2范数和无穷范数。

10.内积
上面介绍了信号是向量,单个信号的定量分析(强度等)由范数规定。下面,我们介绍一对信号的定量分析,(作用巨大而且非常常见的方法)。

信号的转置:行与列进行交换。
如果将转置与共轭操作放在一起(这个操作很有用),就叫做复数转置(厄米特转置),使用H进行表示先进行转置,然后将每个分量进行取共轭操作,用*号表示。实数的共轭转置就是普通的转置咯。

复数乘法法则:(a+bi)(c+di)=(ac-bd)+(bc+ad)i。所以,复数与其共轭相乘等于一个实数。
内积的定义中,后面的向量要进行共轭转置,复数空间的时候,虚数部分符号取反;实数空间的时候,与普通的转置相同)。实数向量的内积是个值(标量),而复数向量的内积仍然是个复数(标量,例如x和y一个实数向量,一个虚数向量)。但是这种定义可以保证复数向量自己本身的内积是个正数。
实数信号中,角度等于内积与两个向量的2范数的相除。复数信号中稍微复杂,角度等于内积的实数部分与两个向量的2范数的相除。注意 注意 注意 复数内积夹角的求法。
内积就表示两个向量的相似程度,虽然计算时使用x[n]与y[n]*的乘积,但是它表示的是x[n]与y[n]的内积,<x[n],y[n]>

应用举例:

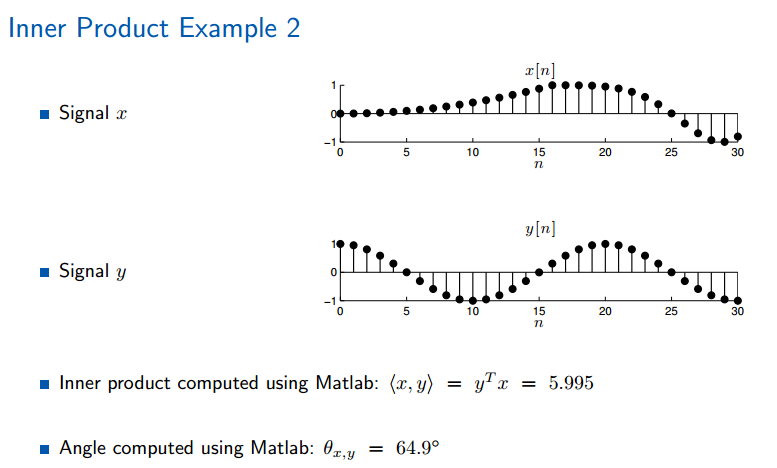
每个信号本身的内积就是该信号的2范数。(实数与复数皆一样)

正交向量:如果两个向量正交,则他们的内积为0
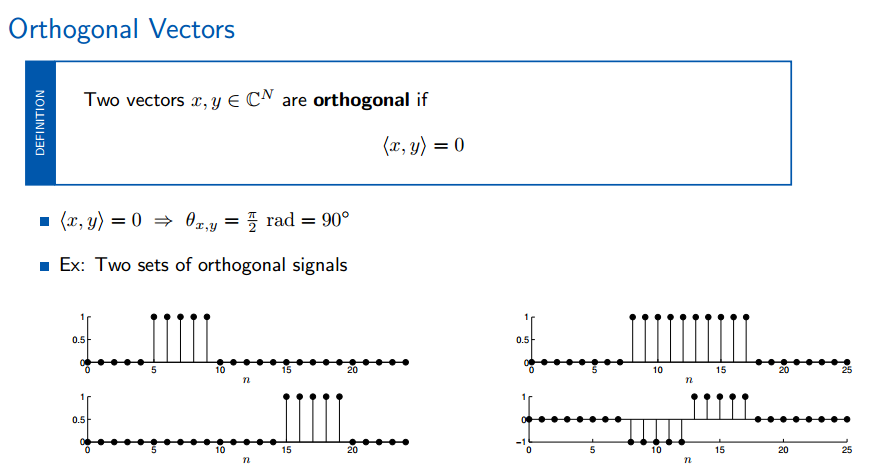
谐波正弦是正交的。(谐波正弦表示改离散时域正弦信号为周期信号的情况,即角频率omega为:(2*pi*k)/N,N是周期)。 注意离散时域正弦的定义,注意离散时域正弦的定义,注意离散时域正弦的定义。
注意:exp^j*2*pi*k = 1 因为,exp^j*2*pi*k = cos(2*pi*k)+j*sin(2*pi*k)

谐波正弦信号的2范数为sqrt(N),其中N为信号长度。它的归一化如下:

总结:
内积的定义。内积夹角度定义。谐波正弦信号是正交的。

11.矩阵相乘和内积
信号的线性组合就是矩阵与向量的乘积,而线性组合也可以表示为两个向量的内积。


多个不同信号,在时间n进行混合,得到的值y[n]为:X矩阵的第n行与权值的内积。复数向量的内积计算需要共轭转置,所以用T表达是不准确的。

总结:
矩阵与向量相乘也是向量内积。

12.柯西不等式
内积和角度这两个有用的工具可以帮助我们对信号进行比较。Amazing的是,柯西不等式可以对这个比较进行定量分析。

通过夹角得到了柯西不等式,得到结论:内积体现了两个信号的相似程度。

柯西不等式很重要,柯西不等式很重要,柯西不等式很重要。两个信号共线,则他们的相似程度最高。一个信号就是另一个信号的缩放(哇哇哇,太神奇)。(想想他们的信号长度N相同,经过alpha的缩放。)

应用举例:大前提:所有信号在传输过程中,都有噪音的影响。
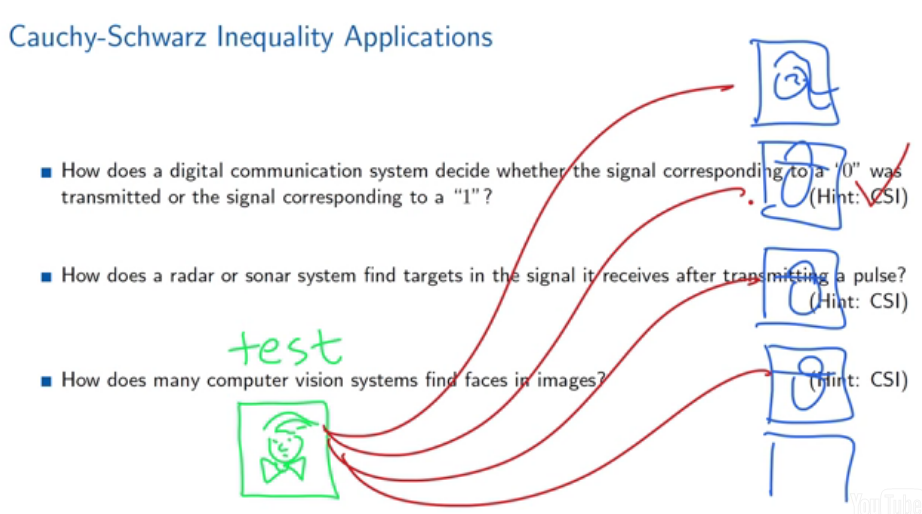
如何识别通讯信号中的0和1? 因为实际波形噪音严重,但是通过与理想信号(0和1)进行内积,就能得到该信号属于0或者1的可能性的大小。

雷达发出一个冲击信号,同时不断接受各种信号(纯噪音,各种信号与噪音的负荷信号),同样进行不断的内积,如果发现了较大的内积值,就是我们想要的结果了。根据延时信息还可以得到该信号(飞机)的速度信息。
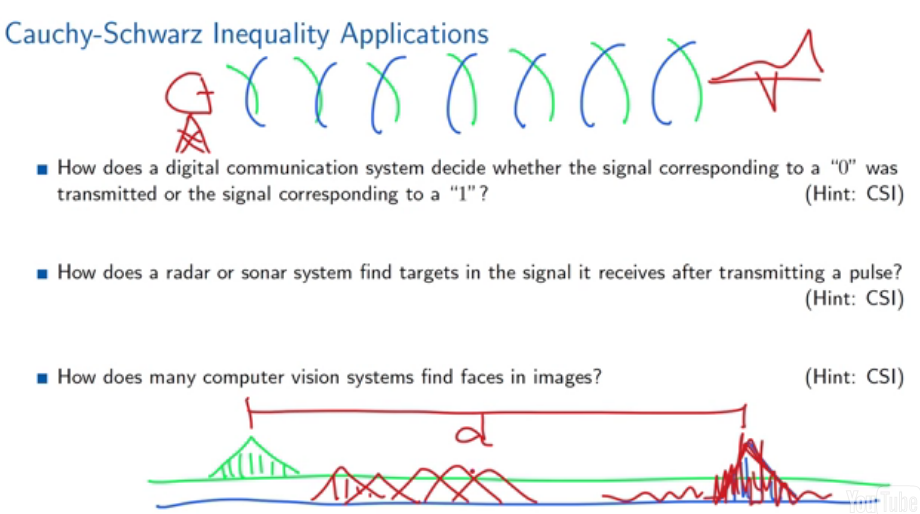
面部识别:最简单的是图像的所有点都进行了注册,所以信号的长度相等,对应分量位置表示相同的信息。所以内积可以表示两个图像的相似程度。(实际识别复杂的多)
总结:
内积可以衡量两个信号的相似程度。
柯西不等式对这种衡量进行了校准,结果在0,1之间。信号接近边界分别表示了不同和相似。

13.长度无限的向量(信号)
以上,我们研究的对象都是有限长度的信号,包括实数和复数两种信号,并研究了他们的范式,内积和线性组合。下面,我们看看无限长的信号。信号的分量标示n从负无穷到正无穷之间。

先看看超级有用的2范数。 从有限到无限,范数的定义没有变化。但是,在无限长度信号中,不一定存在2范数~~~~~~

例如,下面信号的2范数表示该信号: 能量无限能量无限能量无限 哈哈我疯了。
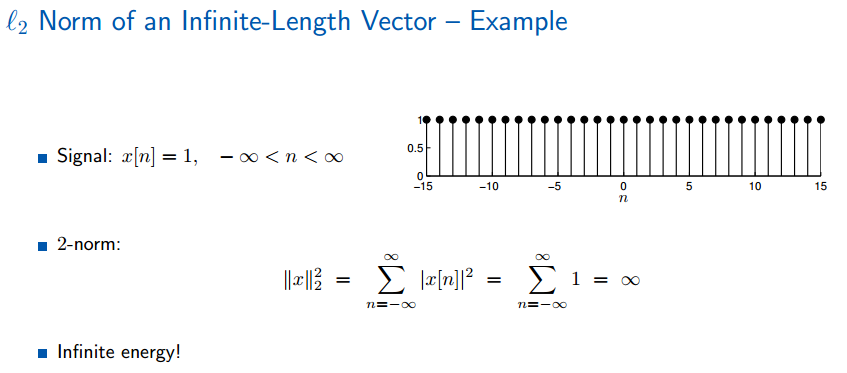
推广到p_norm,也不是所有的无限信号都有P范数。

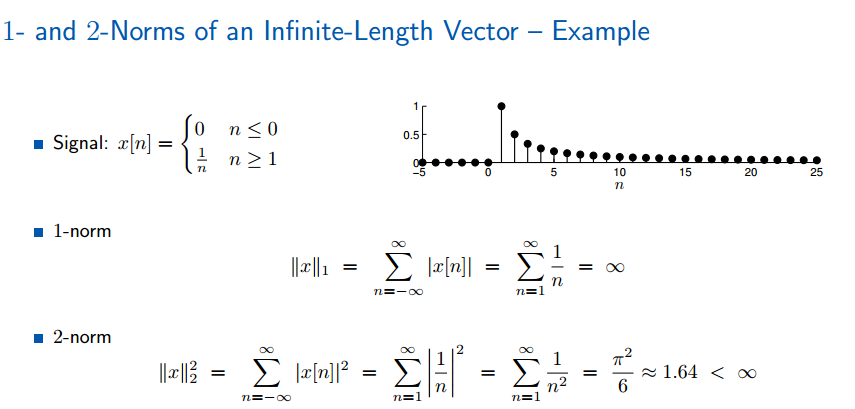
无穷范数呢?

内积的定义与有限信号相比,也没有变化噢。

无限信号的内积与线性组合关系十分紧密,并且与有线信号的线性组合是一样的。 更重要的是:我们对很多无限信号的线性组合非常关注。



总结:
无限信号的范数,内积,线性组合与有限信号完全一样。
BUT, 无限信号存在1范数,2范数,无穷范数不存在的情况。另外,线性组合中可能涉及到无穷种信号的混合(而不单单是信号长度为无穷)
