These are vectors:
They can be multiplied using the "Dot Product" (also see Cross Product).
Calculating
You can calculate the Dot Product of two vectors this way:
a · b = |a| × |b| × cos(θ)
Where:
|a| is the magnitude (length) of vector a
|b| is the magnitude (length) of vector b
θ is the angle between a and b
So we multiply the length of a times the length of b, then multiply by the cosine of the angle between a and b
OR you can calculate it this way:
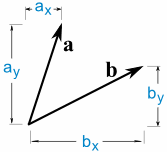
a · b = ax × bx + ay × by
So we multiply the x's, multiply the y's, then add.
Both methods work!
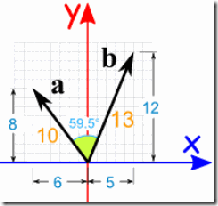
Example: Calculate the dot product of vectors a and b:
a · b = |a| × |b| × cos(θ)
a · b = 10 × 13 × cos(59.5°)
a · b = 10 × 13 × 0.5075...
a · b = 65.98... = 66 (rounded)
a · b = ax × bx + ay × by
a · b = -6 × 5 + 8 × 12
a · b = -30 + 96
a · b = 66
Both methods came up with the same result (after rounding)
Also note that we used minus 6 for ax (it is heading in the negative x-direction)
Note: you can use the Vector Calculator to help you.
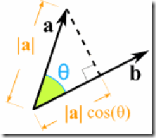
Why cos(θ) ?
OK, to multiply two vectors it makes sense to multiply their lengths together but only when they point in the same direction.
So we make one "point in the same direction" as the other by multiplying by cos(θ):
We take the component of a
that lies alongside b
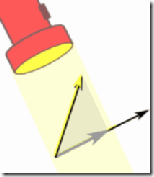
Like shining a light to see
where the shadow lies
THEN we multiply !
It works exactly the same if we "projected" b alongside a then multiplied:
Because it doesn't matter which order we do the multiplication:
|a| × |b| × cos(θ) = |a| × cos(θ) × |b|
Right Angles
When two vectors are at right angles to each other the dot product is zero.
Example: calculate the Dot Product for:
a · b = |a| × |b| × cos(θ)
a · b = | a| × | b| × cos(90°)
a · b = | a| × | b| × 0
a · b = 0
a · b = ax × bx + ay × by
a · b = -12 × 12 + 16 × 9
a · b = -144 + 144
a · b = 0
This can be a handy way to find out if two vectors are at right angles.
Three or More Dimensions
This all works fine in 3 (or more) dimensions, too.
And can actually be very useful!
Example: Sam has measured the end-points of two poles, and wants to know the angle between them:
We have 3 dimensions, so don't forget the z-components:
a · b = ax × bx + ay × by + az × bz
a · b = 9 × 4 + 2 × 8 + 7 × 10
a · b = 36 + 16 + 70
a · b = 122
Now for the other formula:
a · b = |a| × |b| × cos(θ)
But what is |a| ? It is the magnitude, or length, of the vector a. We can use Pythagoras:
- |a| = √(42 + 82 + 102)
- |a| = √(16 + 64 + 100)
- |a| = √180
Likewise for |b|:
- |b| = √(92 + 22 + 72)
- |b| = √(81 + 4 + 49)
- |b| = √134
And we know from the calculation above that a · b = 122, so:
a · b = |a| × |b| × cos(θ)
122 = √180 × √134 × cos(θ)
cos(θ) = 122 / (√180 × √134)
cos(θ) = 0.7855...
θ = cos -1(0.7855...) = 38.2...°
Done!
I tried a calculation like that once, but worked all in angles and distances ... it was very hard, involved lots of trigonometry, and my brain hurt. The method above is much easier.
Cross Product
The Dot Product gives a scalar (ordinary number) answer, and is sometimes called the scalar product.
But there is also the Cross Product which gives a vector as an answer, and is sometimes called the vector product.