[NOI 2007]社交网络

题目大意：给你一个无向图，每个节点的重要值为任意两个节点（三个节点互不相同）相连时通过这个节点的可能性，求出每个节点的重要值

即：

令Cs,t表示从s到t的不同的最短路的数目，Cs,t(v)表示经过v从s到t的最短路的数目；则定义

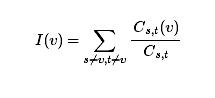
为结点v在社交网络中的重要程度。

题解：用变形的floyd，先求出i->j的道路数，然后枚举i和j求出答案

卡点：
　　1.k忘记移动到循环外面（现在用的是i，我懒得改了）

　　2.在初始for循环中，把j的范围写成了1~m

C++ Code：

sum[b][a]=1;
	}
	for (int i=1;i<=n;i++){
		for (int j=1;j<=n;j++){
			if (!(i^j))continue;
			for (int k=1;k<=n;k++){
				if (!((i^k)&&(j^k)))continue;
				if (res[j][k]==res[j][i]+res[i][k])sum[j][k]+=sum[j][i]*sum[i][k];
				if (res[j][k]>res[j][i]+res[i][k]){
					res[j][k]=res[j][i]+res[i][k];
					sum[j][k]=sum[j][i]*sum[i][k];
				}
			}
		}
	}
	for (int i=1;i<=n;i++){
		for (int j=1;j<=n;j++){
			if (!(i^j))continue;
			for (int k=1;k<=n;k++){
				if (!((i^k)&&(j^k)))continue;
				if (sum[j][k]==0)continue;
				if (res[j][k]==res[j][i]+res[i][k])ans[i]+=(double)(sum[j][i]*sum[i][k])/sum[j][k];
			}
		}
		printf("%.3lf
",ans[i]);
	}
	return 0;
}