LOJ6436 [PKUSC2018] 神仙的游戏 【FFT】

题目分析：

题目要求前后缀相同，把串反过来之后是一个很明显的卷积的形式。这样我们可以完成初步判断(即可以知道哪些必然不行)。

然后考虑一下虽然卷积结果成立，但是存在问号冲突的情况。

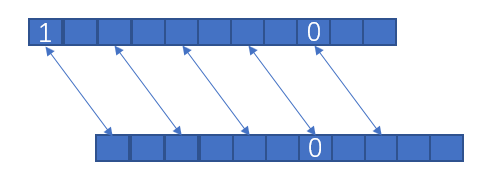
箭头之间应当不存在1。不然就和图上所画的一样。注意到它每隔len个跳一次，所以相当于调和级数，利用原有信息判断即可。

字符串转化的方式有很多种。

代码：

#include<bits/stdc++.h>
using namespace std;

const int maxn = (1<<19)+5;

const int mod = 998244353;
const int gg = 3;

char str[maxn];

int n,m,len,a[maxn<<1],b[maxn<<1],ord[maxn<<1];

int f[maxn<<1],iv;

int fast_pow(int now,int pw){
    int ans = 1,dd = now,bit = 1;
    while(bit <= pw){
    if(bit & pw) {ans = (1ll*ans*dd)%mod;}
    dd = (1ll*dd*dd)%mod;
    bit<<=1;
    }
    return ans;
}

void fft(int *d,int dr){
    for(register int i=0;i<m;i++) if(i < ord[i]) swap(d[i],d[ord[i]]);
    for(register int i=1;i<m;i<<=1){
    int wn = fast_pow(gg,(mod-1)/(2*i));
    if(dr == -1) wn = fast_pow(wn,mod-2);
    for(register int j=0;j<m;j+=(i<<1)){
        for(register int k=0,w=1;k<i;k++,w = (1ll*w*wn)%mod){
        int x = d[j+k],y = (1ll*w*d[j+k+i])%mod;
        d[j+k] = x+y; d[j+k] >=mod?d[j+k]-=mod:1;
        d[j+k+i] = x-y;
        d[j+k+i] < 0?d[j+k+i]+=mod:1;
        }
    }
    }
    if(dr == -1){
    for(register int i=0;i<m;i++) d[i] = (1ll*d[i]*iv)%mod;
    }
}

void work(){
    int n = strlen(str);m = 1;
    while(m < 2*n){m<<=1;len++;} iv = fast_pow(m,mod-2);
    for(register int i=0;i<m;i++) ord[i] = (ord[i>>1]>>1)+((i&1)<<len-1);

    for(register int i=0;i<n;i++) {
    if(str[i] == '0') a[i] = 1;
    else if(str[i] == '1') b[n-i-1] = 1;
    }
    
    fft(a,1); fft(b,1); 
    for(register int i=0;i<m;i++) {
    f[i] = (1ll*a[i]*b[i])%mod;
    }
    
    memset(a,0,sizeof(a)); memset(b,0,sizeof(b));
    
    for(register int i=0;i<n;i++) {
    if(str[i] == '1') a[i] = 1;
    else if(str[i] == '0') b[n-i-1] = 1;
    }
    
    fft(a,1); fft(b,1); 
    for(register int i=0;i<m;i++) {
    f[i] += (1ll*a[i]*b[i])%mod; if(f[i] >mod)f[i]-=mod;
    }
    
    fft(f,-1);

    for(register int i=0;i<n-1;i++){
    int now = n-1-i;
    for(register int j=i-now;j>=0;j-=now){
        f[i] |= f[j];
    }
    }

    long long ans = 0;
    for(register int i=1;i<=n;i++){
    ans ^= (1ll*(f[i-1]==0)*i*i);
    }
    printf("%lld",ans);
}

int main(){
    scanf("%s",str);
    work();
    return 0;
}