题面
题目链接
题目描述
给定一棵 $ n $个节点的树,有两个操作:
CHANGE $ i $ $ t_i $ 把第 $ i $条边的边权变成 $ t_i $
QUERY $ a $ $ b $ 输出从 $ a $ 到 $ b $ 的路径中最大的边权,当 $ a=b $ 的时候,输出 0
输入输出格式
输入格式:
第一行输入一个 $ n $,表示节点个数
第二行到第 $ n $ 行每行输入三个数,$ u_i,v_i,w_i $ ,分别表示 $ u_i,v_i $ 有一条边,边权是 $ w_i $
第 $ n+1 $ 行开始,一共有不定数量行,每一行分别有以下三种可能
CHANGE,QUERY同题意所述
DONE表示输入结束
输出格式:
对于每个QUERY操作,输出一个数,表示 $ a $ $ b $ 之间边权最大值
输入输出样例
输入样例:
3
1 2 1
2 3 2
QUERY 1 2
CHANGE 1 3
QUERY 1 2
DONE
输出样例:
1
3
3
说明
【数据范围】
$1 leq n leq 10^5 $
操作次数 $ leq 3*10^5 $
$ w_i $ 和 $ t_i leq 2^{31}-1$
说明
【时空限制】
1000ms,512M
思路
熟知的 树链剖分 是解决点权的问题的,而这一题是边权。
由于每个点可以有多个儿子,但只有一个父亲,可以考虑将边权存储到深度较大的点的点权。这样n-1条边的边权就会对应到n-1个点上,而根节点(这里以1为根节点)的点权就是0。
再考虑题中两个操作。
Change
Change操作相对简单。改变两点之间的边权,即改动两点中较深点的点权。
Query
Query操作略有改动。查询两点间路径中所有边的最大边权,如果查询所有经过的点是有问题的。先看图
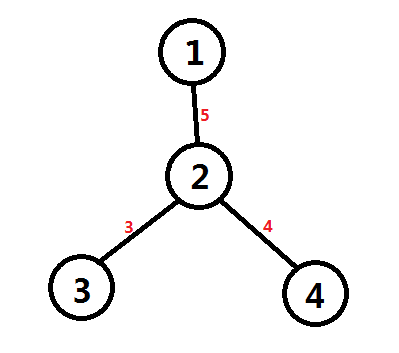
要查询3,4两点间所有边的最大边权,如果取点3,2,4点权的最大值,那么答案是5,显然是错误的,因为点2记录的是他与他父亲之间的边权,这是肯定不会经过的边。故在统计答案时,不能统计两点的LCA。联系树剖的基本操作(其中Q为在线段树上查询最大值)
int Ask(int u,int v)
{
int ans=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
ans=max(ans,Q(1,nid[top[u]],nid[u]));
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
ans=max(ans,Q(1,nid[u],nid[v]));
return ans;
}
其中while循环不用改变,while循环结束后,u和v处于同一条链上。
如果u==v,此时u和v都是最初两点的LCA,此时直接返回
否则,u和v之中深度较小的那一点是最初两点的LCA,应该从这个点的重儿子开始统计答案。
故改变后的代码如下
int Ask(int u,int v)
{
int ans=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
ans=max(ans,Q(1,nid[top[u]],nid[u]));
u=fa[top[u]];
}
if(u==v) return ans;
if(dep[u]>dep[v]) swap(u,v);
ans=max(ans,Q(1,nid[u]+1,nid[v]));
return ans;
}
AC代码
#include<bits/stdc++.h>
const int maxn=100010;
using namespace std;
int n,wt[maxn];
int tot,to[maxn<<1],nxt[maxn<<1],head[maxn];
int dep[maxn],len[maxn],fa[maxn],son[maxn];
int cnt,nid[maxn],nw[maxn],top[maxn];
struct SegmentTree
{
int l,r,mx;
#define l(a) tree[a].l
#define r(a) tree[a].r
#define m(a) ((l(a)+r(a))>>1)
#define mx(a) tree[a].mx
}tree[maxn<<2];
void dfs1(int u,int f,int d)
{
dep[u]=d;fa[u]=f;len[u]=1;
int maxson=-1;
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(v==f) continue;
dfs1(v,u,d+1);
len[u]+=len[v];
if(len[v]>maxson) maxson=len[v],son[u]=v;
}
}
void dfs2(int p,int t)
{
nid[p]=++cnt;
top[p]=t;
if(!son[p]) return;
dfs2(son[p],t);
for(int i=head[p];i;i=nxt[i])
{
int v=to[i];
if(v==fa[p] || v==son[p]) continue;
dfs2(v,v);
}
}
void BuildTree(int p,int l,int r)
{
l(p)=l;r(p)=r;
if(l==r)
{
mx(p)=nw[l];
return;
}
BuildTree(p<<1,l(p),m(p));
BuildTree(p<<1|1,m(p)+1,r);
mx(p)=max(mx(p<<1),mx(p<<1|1));
}
void Change(int np,int p,int k)
{
if(l(np)==r(np))
{
mx(np)=k;
return;
}
if(p<=m(np)) Change(np<<1,p,k);
if(p>m(np)) Change(np<<1|1,p,k);
mx(np)=max(mx(np<<1),mx(np<<1|1));
}
int Q(int p,int l,int r)
{
if(l<=l(p) && r>=r(p)) return mx(p);
int ans=0;
if(l<=m(p)) ans=max(ans,Q(p<<1,l,r));
if(r>m(p)) ans=max(ans,Q(p<<1|1,l,r));
return ans;
}
int Ask(int u,int v)
{
int ans=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
ans=max(ans,Q(1,nid[top[u]],nid[u]));
u=fa[top[u]];
}
if(u==v) return ans;
if(dep[u]>dep[v]) swap(u,v);
ans=max(ans,Q(1,nid[u]+1,nid[v]));
return ans;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<n;i++)
{
int u,v,w;scanf("%d%d%d",&u,&v,&w);wt[i]=w;
to[++tot]=v;nxt[tot]=head[u];head[u]=tot;
to[++tot]=u;nxt[tot]=head[v];head[v]=tot;
}
dfs1(1,1,1);
dfs2(1,1);
for(int i=1;i<n;i++)
{
int u=to[2*i-1],v=to[2*i];
if(dep[u]>dep[v]) nw[nid[u]]=wt[i];
else nw[nid[v]]=wt[i];
}
BuildTree(1,1,n);
while(1)
{
string way;cin>>way;if(way=="DONE") break;
if(way=="CHANGE")
{
int i,k;scanf("%d%d",&i,&k);
int u=to[2*i-1],v=to[2*i];
if(dep[u]>dep[v]) Change(1,nid[u],k);
else Change(1,nid[v],k);
}
if(way=="QUERY")
{
int u,v;scanf("%d%d",&u,&v);
printf("%d
",Ask(u,v));
}
}
return 0;
}
总结
树剖处理边权的板子题