zoukankan html css js c++ java

二叉搜索树Java实现（查找、插入、删除、遍历）

　　由于最近想要阅读下 JDK1.8 中 HashMap 的具体实现，但是由于 HashMap 的实现中用到了红黑树，所以我觉得有必要先复习下红黑树的相关知识，所以写下这篇随笔备忘，有不对的地方请指出～

　　学习红黑树，我觉得有必要从二叉搜索树开始学起，本篇随笔就主要介绍 Java 实现二叉搜索树的查找、插入、删除、遍历等内容。

　　二叉搜索树需满足以下四个条件：

若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
任意节点的左、右子树也分别为二叉查找树；
没有键值相等的节点。

　　二叉搜索树举例：

　　　　　　　　　　　　　　　　　　　　　　　　　图一

　　接下来将基于图一介绍二叉搜索树相关操作。

　　首先，应先有一个节点对象相关的类，命名为 Node。

 1 class Node {
 2     int key;
 3     int value;
 4     Node leftChild;
 5     Node rightChild;
 6 
 7     public Node(int key, int value) {
 8         this.key = key;
 9         this.value = value;
10     }
11 
12     public void displayNode() {
13 
14     }
15 }

　　Node 类中包含 key 值，用于确定节点在树中相应位置，value 值代表要存储的内容，还含有指向左右孩子节点的两个引用。

　　接下来看下搜索树相应的类：

 1 class Tree {
 2     Node root;//保存树的根
 3 
 4     public Node find(int key) {//查找指定节点
 5         
 6     }
 7 
 8     public void insert(int key, int value) {//插入节点
 9        
10     }
11 
12     public boolean delete(int key) {//删除指定节点
13         
14     }
15 
16     private Node getDirectPostNode(Node delNode) {//得到待删除节点的直接后继节点
17         
18     }
19 
20     public void preOrder(Node rootNode) {//先序遍历树
21        
22     }
23 
24     public void inOrder(Node rootNode) {//中序遍历树
25         
26     }
27 
28     public void postOrder(Node rootNode) {//后序遍历树
29         
30     }
31 }

　　　类中表示树的框架，包含查找、插入、遍历、删除相应方法，其中删除节点操作最为复杂，接下来一一介绍。

　　一、查找某个节点

　　　　由于二叉搜索树定义上的特殊性，只需根据输入的 key 值从根开始进行比较，若小于根的 key 值，则与根的左子树比较，大于根的key值与根的右子树比较，以此类推，找到则返回相应节点，否则返回 null。

 1 public Node find(int key) {
 2         Node currentNode = root;
 3         while (currentNode != null && currentNode.key != key) {
 4             if (key < currentNode.key) {
 5                 currentNode = currentNode.leftChild;
 6             } else {
 7                 currentNode = currentNode.rightChild;
 8             }
 9         }
10         return currentNode;
11 }

　　　二、插入节点

　　　　与查找操作相似，由于二叉搜索树的特殊性，待插入的节点也需要从根节点开始进行比较，小于根节点则与根节点左子树比较，反之则与右子树比较，直到左子树为空或右子树为空，则插入到相应为空的位置，在比较的过程中要注意保存父节点的信息及待插入的位置是父节点的左子树还是右子树，才能插入到正确的位置。

 1 public void insert(int key, int value) {
 2         if (root == null) {
 3             root = new Node(key, value);
 4             return;
 5         }
 6         Node currentNode = root;
 7         Node parentNode = root;
 8         boolean isLeftChild = true;
 9         while (currentNode != null) {
10             parentNode = currentNode;
11             if (key < currentNode.key) {
12                 currentNode = currentNode.leftChild;
13                 isLeftChild = true;
14             } else {
15                 currentNode = currentNode.rightChild;
16                 isLeftChild = false;
17             }
18         }
19         Node newNode = new Node(key, value);
20         if (isLeftChild) {
21             parentNode.leftChild = newNode;
22         } else {
23             parentNode.rightChild = newNode;
24         }
25 }

　　　　三、遍历二叉搜索树

　　　　遍历操作与遍历普通二叉树操作完全相同，不赘述。

 1     public void preOrder(Node rootNode) {
 2         if (rootNode != null) {
 3             System.out.println(rootNode.key + " " + rootNode.value);
 4             preOrder(rootNode.leftChild);
 5             preOrder(rootNode.rightChild);
 6         }
 7     }
 8 
 9     public void inOrder(Node rootNode) {
10         if (rootNode != null) {
11             inOrder(rootNode.leftChild);
12             System.out.println(rootNode.key + " " + rootNode.value);
13             inOrder(rootNode.rightChild);
14         }
15     }
16 
17     public void postOrder(Node rootNode) {
18         if (rootNode != null) {
19             postOrder(rootNode.leftChild);
20             postOrder(rootNode.rightChild);
21             System.out.println(rootNode.key + " " + rootNode.value);
22         }
23     }

　　　　四、删除指定节点。

　　　　在二叉搜索树中删除节点操作较复杂，可分为以下三种情况。

　　　　1、待删除的节点为叶子节点，可直接删除。

　　public boolean delete(int key) {
        Node currentNode = root;//用来保存待删除节点
        Node parentNode = root;//用来保存待删除节点的父亲节点
        boolean isLeftChild = true;//用来确定待删除节点是父亲节点的左孩子还是右孩子
        while (currentNode != null && currentNode.key != key) {
            parentNode = currentNode;
            if (key < currentNode.key) {
                currentNode = currentNode.leftChild;
                isLeftChild = true;
            } else {
                currentNode = currentNode.rightChild;
                isLeftChild = false;
            }
        }
        if (currentNode == null) {
            return false;
        }
        if (currentNode.leftChild == null && currentNode.rightChild == null) {//要删除的节点为叶子节点
            if (currentNode == root)
                root = null;
            else if (isLeftChild)
                parentNode.leftChild = null;
            else
                parentNode.rightChild = null;
        } 
        ......
    
    }

　　　　2、待删除节点只有一个孩子节点

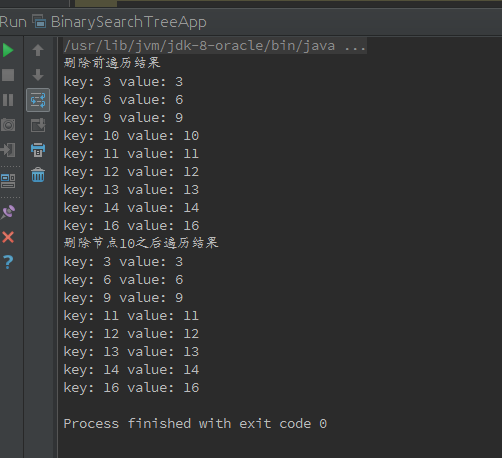
　　　　例如删除图一中的 key 值为 11 的节点，只需将 key 值为 13 的节点的左孩子指向 key 值为 12的节点即可达到删除 key 值为 11 的节点的目的。

　　　　由以上分析可得代码如下（接上述 delete 方法省略号后）：

 1         else if (currentNode.rightChild == null) {//要删除的节点只有左孩子
 2             if (currentNode == root)
 3                 root = currentNode.leftChild;
 4             else if (isLeftChild)
 5                 parentNode.leftChild = currentNode.leftChild;
 6             else
 7                 parentNode.rightChild = currentNode.leftChild;
 8         } else if (currentNode.leftChild == null) {//要删除的节点只有右孩子
 9             if (currentNode == root)
10                 root = currentNode.rightChild;
11             else if (isLeftChild)
12                 parentNode.leftChild = currentNode.rightChild;
13             else
14                 parentNode.rightChild = currentNode.rightChild;
15         } 
           ......

　　　　3、待删除节点既有左孩子，又有右孩子。

　　　　例如删除图一中 key 值为 10 的节点，这时就需要用 key 值为 10 的节点的中序后继节点（节点 11）来代替 key 值为 10 的节点，并删除 key 值为 10 的节点的中序后继节点，由中序遍历相关规则可知， key 值为 10 的节点的直接中序后继节点一定是其右子树中 key 值最小的节点，所以此中序后继节点一定不含子节点或者只含有一个右孩子，删除此中序后继节点就属于上述 1,2 所述情况。图一中 key 值为 10 的节点的直接中序后继节点为 11，节点 11 含有一个右孩子 12。

　　　　所以删除图一中 key 值为 10 的节点分为以下几步：

　　　　a、找到 key 值为 10 的节点的直接中序后继节点（即其右子树中值最小的节点 11），并删除此直接中序后继节点。

 1  private Node getDirectPostNode(Node delNode) {//方法作用为得到待删除节点的直接后继节点
 2         
 3         Node parentNode = delNode;//用来保存待删除节点的直接后继节点的父亲节点
 4         Node direcrPostNode = delNode;//用来保存待删除节点的直接后继节点
 5         Node currentNode = delNode.rightChild;
 6         while (currentNode != null) {
 7             parentNode = direcrPostNode;
 8             direcrPostNode = currentNode;
 9             currentNode = currentNode.leftChild;
10         }
11         if (direcrPostNode != delNode.rightChild) {//从树中删除此直接后继节点
12             parentNode.leftChild = direcrPostNode.rightChild;
13             direcrPostNode.rightChild = null;
14         }
15         return direcrPostNode;//返回此直接后继节点
16         
17 }

　　　　b、将此后继节点的 key、value 值赋给待删除节点的 key，value值。(接情况二中省略号代码之后)

1 else { //要删除的节点既有左孩子又有右孩子
2 
3             //思路：用待删除节点右子树中的key值最小节点的值来替代要删除的节点的值,然后删除右子树中key值最小的节点
4             //右子树key最小的节点一定不含左子树,所以删除这个key最小的节点一定是属于叶子节点或者只有右子树的节点
5             Node directPostNode = getDirectPostNode(currentNode);
6             currentNode.key = directPostNode.key;
7             currentNode.value = directPostNode.value;
8 
9 }

　　至此删除指定节点的操作结束。

　　最后给出完整代码及简单测试代码及测试结果：

  1 class Node {
  2     int key;
  3     int value;
  4     Node leftChild;
  5     Node rightChild;
  6 
  7     public Node(int key, int value) {
  8         this.key = key;
  9         this.value = value;
 10     }
 11 
 12     public void displayNode() {
 13 
 14     }
 15 }
 16 
 17 class Tree {
 18     Node root;
 19 
 20     public Node find(int key) {
 21         Node currentNode = root;
 22         while (currentNode != null && currentNode.key != key) {
 23             if (key < currentNode.key) {
 24                 currentNode = currentNode.leftChild;
 25             } else {
 26                 currentNode = currentNode.rightChild;
 27             }
 28         }
 29         return currentNode;
 30     }
 31 
 32     public void insert(int key, int value) {
 33         if (root == null) {
 34             root = new Node(key, value);
 35             return;
 36         }
 37         Node currentNode = root;
 38         Node parentNode = root;
 39         boolean isLeftChild = true;
 40         while (currentNode != null) {
 41             parentNode = currentNode;
 42             if (key < currentNode.key) {
 43                 currentNode = currentNode.leftChild;
 44                 isLeftChild = true;
 45             } else {
 46                 currentNode = currentNode.rightChild;
 47                 isLeftChild = false;
 48             }
 49         }
 50         Node newNode = new Node(key, value);
 51         if (isLeftChild) {
 52             parentNode.leftChild = newNode;
 53         } else {
 54             parentNode.rightChild = newNode;
 55         }
 56     }
 57 
 58     public boolean delete(int key) {
 59         Node currentNode = root;
 60         Node parentNode = root;
 61         boolean isLeftChild = true;
 62         while (currentNode != null && currentNode.key != key) {
 63             parentNode = currentNode;
 64             if (key < currentNode.key) {
 65                 currentNode = currentNode.leftChild;
 66                 isLeftChild = true;
 67             } else {
 68                 currentNode = currentNode.rightChild;
 69                 isLeftChild = false;
 70             }
 71         }
 72         if (currentNode == null) {
 73             return false;
 74         }
 75         if (currentNode.leftChild == null && currentNode.rightChild == null) {
 76             //要删除的节点为叶子节点
 77             if (currentNode == root)
 78                 root = null;
 79             else if (isLeftChild)
 80                 parentNode.leftChild = null;
 81             else
 82                 parentNode.rightChild = null;
 83         } else if (currentNode.rightChild == null) {//要删除的节点只有左孩子
 84             if (currentNode == root)
 85                 root = currentNode.leftChild;
 86             else if (isLeftChild)
 87                 parentNode.leftChild = currentNode.leftChild;
 88             else
 89                 parentNode.rightChild = currentNode.leftChild;
 90         } else if (currentNode.leftChild == null) {//要删除的节点只有右孩子
 91             if (currentNode == root)
 92                 root = currentNode.rightChild;
 93             else if (isLeftChild)
 94                 parentNode.leftChild = currentNode.rightChild;
 95             else
 96                 parentNode.rightChild = currentNode.rightChild;
 97         } else { //要删除的节点既有左孩子又有右孩子
 98             //思路：用待删除节点右子树中的key值最小节点的值来替代要删除的节点的值,然后删除右子树中key值最小的节点
 99             //右子树key最小的节点一定不含左子树,所以删除这个key最小的节点一定是属于叶子节点或者只有右子树的节点
100             Node directPostNode = getDirectPostNode(currentNode);
101             currentNode.key = directPostNode.key;
102             currentNode.value = directPostNode.value;
103         }
104         return true;
105     }
106 
107     private Node getDirectPostNode(Node delNode) {//方法作用为得到待删除节点的直接后继节点
108 
109         Node parentNode = delNode;//用来保存待删除节点的直接后继节点的父亲节点
110         Node direcrPostNode = delNode;//用来保存待删除节点的直接后继节点
111         Node currentNode = delNode.rightChild;
112         while (currentNode != null) {
113             parentNode = direcrPostNode;
114             direcrPostNode = currentNode;
115             currentNode = currentNode.leftChild;
116         }
117         if (direcrPostNode != delNode.rightChild) {//从树中删除此直接后继节点
118             parentNode.leftChild = direcrPostNode.rightChild;
119             direcrPostNode.rightChild = null;
120         }
121         return direcrPostNode;//返回此直接后继节点
122 
123     }
124 
125     public void preOrder(Node rootNode) {
126         if (rootNode != null) {
127             System.out.println(rootNode.key + " " + rootNode.value);
128             preOrder(rootNode.leftChild);
129             preOrder(rootNode.rightChild);
130         }
131     }
132 
133     public void inOrder(Node rootNode) {
134         if (rootNode != null) {
135             inOrder(rootNode.leftChild);
136             System.out.println("key: " + rootNode.key + " " + "value: " + rootNode.value);
137             inOrder(rootNode.rightChild);
138         }
139     }
140 
141     public void postOrder(Node rootNode) {
142         if (rootNode != null) {
143             postOrder(rootNode.leftChild);
144             postOrder(rootNode.rightChild);
145             System.out.println(rootNode.key + " " + rootNode.value);
146         }
147     }

    　　private void destroy(Node tree) {
     　　    if (tree==null)
     　　        return ;
 
       　　  if (tree.left != null)
      　　       destroy(tree.leftChild);
      　　   if (tree.right != null)
       　　      destroy(tree.rightChild);
 
      　　  tree=null;
  　　  }
　　　　
　　　　public void destory() {
　　　　　　destory(root);
　　　　}

148 } 
149 public class BinarySearchTreeApp { 
150　　 public static void main(String[] args) {
151　　　　　　 Tree tree = new Tree(); 
152　　　　 tree.insert(6, 6);//插入操作,构造图一所示的二叉树 

153　　　　 tree.insert(3, 3); 

154 　　　　tree.insert(14, 14); 

155　　　　 tree.insert(16, 16); 

156　　　　 tree.insert(10, 10); 

157　　　　 tree.insert(9, 9); 

158 　　　　tree.insert(13, 13); 

159　　　　 tree.insert(11, 11); 

160 　　　　tree.insert(12, 12); 

161 162　　 System.out.println("删除前遍历结果"); 

163 　　　　tree.inOrder(tree.root);//中序遍历操作 

164 165　　 System.out.println("删除节点10之后遍历结果"); 

166 　　　　tree.delete(10);//删除操作 

167  　　　　tree.inOrder(tree.root); 168  
　　　　} 

169 }

　　　　测试结果：

查看全文

相关阅读:
dedecmsV5.7和discuz!X3.4整合之后免激活登陆
 dedecms织梦文章微信分享带缩略图与简介
 关于PHP的mkdir函数
 关于discuz的fap.php 漏洞问题
 discuzX3.4安装之后，没有任何样式怎么办？
阿里云 RDS for MySQL支持什么引擎
 PHP随机生成要求位数个字符（大小写字母+数字）
PHP json_decode为什么将json字符串转成数组是对象格式？
PHP实用的功能函数
 css实现三角形图标

原文地址：https://www.cnblogs.com/Michaelwjw/p/6384428.html