震惊!Midoria7 居然是个 nt。为什么呢?快和小编一起来看一看吧~

震惊!Midoria7 竟然直接把正解注释掉,活到爆。


T1: 100 ( ightarrow) 5
T2: 90 ( ightarrow) 50
T3: 50 ( ightarrow) 0
T4: 20 ( ightarrow) 0
T1:Tree
直接输出边权和。

震惊,所以 512 MB 和 2000 ms 都是骗人的。
个人理解:肯定会有一种情况使排列中相邻两数都直接相连答案就取该边边权。如果你用换一种排列,一定会使某些更小的边被更多次取到。
T2:Permutation
直接冒泡 50 pts,然而似乎剪个枝就 90 pts 了。数据居然折磨水。
乱搞的 90 pts Code
#include <bits/stdc++.h>
using namespace std;
const int maxn=5e5+10;
int n,K;
int a[maxn],pos[maxn];
inline int read(){
int x=0;bool fopt=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')fopt=0;
for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-48;
return fopt?x:-x;
}
inline void Swap(int &x,int &y){
int temp=x;x=y;y=temp;
}
int main(){
#ifndef LOCAL
freopen("permutation.in","r",stdin);
freopen("permutation.out","w",stdout);
#endif
n=read();K=read();
for(int i=1;i<=n;i++){
a[i]=read();
pos[a[i]]=i;
}
for(register int T=1;T<=n;T++){
int flag=0;
for(register int i=1;i<=n;i++){
int now=a[i];
if(now!=1&&pos[now-1]-pos[now]>=K){
Swap(a[i],a[pos[now-1]]);
Swap(pos[now],pos[now-1]);
flag=1;
}
}
for(register int i=1;i<=n;i++){
int now=a[i];
if(now!=n&&pos[now]-pos[now+1]>=K){
Swap(a[i],a[pos[now+1]]);
Swap(pos[now],pos[now+1]);
flag=1;
}
}
if(!flag)break;
}
for(int i=1;i<=n;i++)
printf("%d
",a[i]);
return 0;
}
正向字典序最小,等同于逆置换的逆向字典序最大。
引用镇楼。逆置换就是数值和下标互换的序列。
令原排列为 (P),(Q=P^{-1})。那么题目要求的条件就是 (vert Q_i-Q_{i+1}vertgeq K)。
字典序最小,就是 (Q_1) 尽量小,其次 (Q_2) 尽量小,以此类推。
注意到,对于一对 (i) 和 (i+1),如果其 (Q) 差值小于 (K),那他们就永远无法交换。即对于 (Q) 的相邻位,若差值小于 (K),那就永远无法跨越。
那对于两个下标 (i,j) 来说,若 (i<j),且 (vert Q_i-Q_jvert< K),我们就建上边,表示一个不等式条件。整个序列变成了一个 DAG,那么我们用一个拓扑序,满足字典序最小。首先我们肯定不能用普通队列,而是优先队列(见菜肴制作)
正确的操作是:反向建边,每次取最大编号,且拓扑编号从 (n) 到 (1)。(但是目前并不会证为什么和正向拓扑有区别,反正引用了就是对的)
首先,这样建边是 (O(nK)) 的,时间和空间都会炸,显然不能真的建出图来。所以我们考虑用线段树优化。
维护一个 (P) 序列区间最大值线段树,但线段树中记录的是 (Q)。pushup维护一下即可。那么我们考虑入度为 (0) 的点满足什么条件。
返回来看我们的建边条件。对于一个 (vert Q_i-Q_jvert< K) 的下标 ((i,j)),如果一开始 (P_i<P_j),那么最后肯定也是 (P_i<P_j),那么我们反向建图就建了一条 (j ightarrow i) 的边。
那么对于一个下标 (i),如果 (P_i) 是 (P) 序列区间 ([i-K,i+K]) 中的最大值,那么 (i) 一定是入度为 (0) 的点,因为没有比他更大的 (P_j) 了。那我们直接把它入队。
拓扑排序的过程中,我们取出堆顶,然后删除。然后我们检查 ([i-K,i-1]) 和 ([i+1,i+K]) 两个区间,如果入度为 (0),那么也一并入队即可(拓扑排序基本操作)
最后输出答案。所以本题比较有趣的转化就是入度为 (0) 的点的判断。
Code
#include <bits/stdc++.h>
using namespace std;
const int maxn=2e6+10;
int n,K;
int a[maxn],ans[maxn];
inline int read(){
int x=0;bool fopt=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')fopt=0;
for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-48;
return fopt?x:-x;
}
#define lson (rt<<1)
#define rson (rt<<1|1)
int tree[maxn<<2];
inline void pushup(int rt){
tree[rt]=a[tree[lson]]>a[tree[rson]]?tree[lson]:tree[rson];
}
void build(int rt,int l,int r){
if(l==r)return tree[rt]=l,void();
int mid=(l+r)>>1;
build(lson,l,mid);build(rson,mid+1,r);
pushup(rt);
}
void del(int rt,int l,int r,int p){
if(l==r)return tree[rt]=0,void();
int mid=(l+r)>>1;
if(p<=mid)del(lson,l,mid,p);
else del(rson,mid+1,r,p);
pushup(rt);
}
int query(int rt,int l,int r,int s,int t){
if(r<s||l>t)return 0;
if(s<=l&&r<=t)return tree[rt];
int mid=(l+r)>>1;
int L=query(lson,l,mid,s,t),R=query(rson,mid+1,r,s,t);
return a[L]>a[R]?L:R;//若有不合法区间会return 0,由于a[0]=-INF,所以一定不会被取到
}
bool vis[maxn];
priority_queue<int> q;
inline void Push(int u){
if(vis[u])return;
if(query(1,1,n,u-K+1,u+K-1)==u){
q.push(u);vis[u]=1;
}
}
int main(){
#ifndef LOCAL
freopen("permutation.in","r",stdin);
freopen("permutation.out","w",stdout);
#endif
n=read();K=read();a[0]=-0x3f3f3f3f;
for(int i=1;i<=n;i++)
a[i]=read();
build(1,1,n);
for(int i=1;i<=n;i++)
Push(i);
for(int i=n;i>=1;i--){
int u=q.top();q.pop();
ans[u]=i;
del(1,1,n,u);
int pos=query(1,1,n,u-K+1,u-1);
if(pos)Push(pos);
pos=query(1,1,n,u+1,u+K-1);
if(pos)Push(pos);
}
for(int i=1;i<=n;i++)
printf("%d
",ans[i]);
return 0;
}
T3:Graph
震惊,打了 160 行部分分之后爆零,人傻了。
原因是我没用统计方案个数而是耍聪明直接输出 (cfrac{m}{2})。
显然对于一个联通块非常正确,但是数据中居然有这样的数据,人傻了。
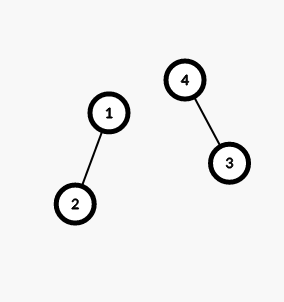
正解基本就是树形态的改一改。我们先想树形态怎么做,显然从下到上,儿子先自己配对,多出来的单个的向上传递,和连父边配对。
int dfs(int u,int fa){
int now=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa)continue;
int temp=dfs(v,u);
if(temp)ans.push_back((Node){temp,v,u});//有从向下传来的节点,先配对
else{
if(now){
ans.push_back((Node){now,u,v});//儿子自己互相配对
now=0;
}else now=v;
}
}
return now;//当now是0,表示该点的儿子都互相配对完了,否则就向上传递
}
所以显然对于每一个联通块都是有一个 dfs 树的。然而不同的就是多了一些非树边,但处理是一样的。我们只需判断一下深度,防止重复即可。
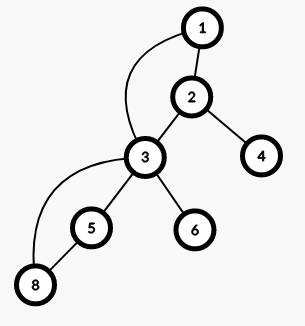
显然对于 3 连接的非树边,我们要去处理 8 而不是 1...
Code
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
const int maxm=2e5+10;
int n,m;
struct Edge{
int from,to,id,nxt;
}e[maxm<<1];
struct Node{
int x,y,z;
};
inline int read(){
int x=0;bool fopt=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-')fopt=0;
for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-48;
return fopt?x:-x;
}
int head[maxn],cnt;
inline void add(int u,int v){
e[++cnt].from=u;
e[cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int dep[maxn];
vector<Node> ans;
int dfs(int u){
int now=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(!dep[v]){
dep[v]=dep[u]+1;
int temp=dfs(v);
if(temp)ans.push_back((Node){temp,v,u});
else{
if(now){
ans.push_back((Node){now,u,v});
now=0;
}else now=v;
}
}else{
if(dep[v]>dep[u]){
if(now){
ans.push_back((Node){now,u,v});
now=0;
}else now=v;
}
}
}
return now;
}
int main(){
#ifndef LOCAL
freopen("graph.in","r",stdin);
freopen("graph.out","w",stdout);
#endif
n=read();m=read();
for(int i=1;i<=m;i++){
int u=read(),v=read();
add(u,v);add(v,u);
}
for(int i=1;i<=n;i++)
if(!dep[i]){
dep[i]=1;dfs(i);
}
printf("%d
",ans.size());
for(int i=0;i<ans.size();i++)
printf("%d %d %d
",ans[i].x,ans[i].y,ans[i].z);
return 0;
}
T4:十字绣
似乎是原题,然而是小假期集训的没做过。
震惊!sb Midoria7 居然不删调试,活到爆。
格点连边,找联通块大小即可。注意边界。
Code
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m,ans;
char s[maxn];
struct Edge{
int from,to,w,nxt;
}e[maxn<<4];
int cnt;
int head[maxn],face[maxn],rear[maxn],f[maxn];
inline int add(int u,int v,int w){
e[++cnt].from=u;
e[cnt].to=v;
w==1?face[u]++:rear[u]++;
f[u]=1;
e[cnt].nxt=head[u];
head[u]=cnt;
}
inline int Get(int x,int y){
return (x-1)*(m+1)+y;
}
inline void add1(int x,int y,int w){// 右上->左下
add(Get(x,y+1),Get(x+1,y),w);
add(Get(x+1,y),Get(x,y+1),w);
}
inline void add2(int x,int y,int w){// 左上->右下
add(Get(x,y),Get(x+1,y+1),w);
add(Get(x+1,y+1),Get(x,y),w);
}
inline void Init(int w){
for(int i=1;i<=n;i++){
scanf("%s",s+1);
for(int j=1;j<=m;j++){
if(s[j]!='.'){
if(s[j]=='/')add1(i,j,w);
else if(s[j]=='X'){
add1(i,j,w);add2(i,j,w);
}else add2(i,j,w);
}
}
}
}
int res;
bool vis[maxn];
void dfs(int u){
vis[u]=1;
res+=abs(face[u]-rear[u]);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(vis[v])continue;
dfs(v);
}
}
int main(){
#ifndef LOCAL
freopen("stitch.in","r",stdin);
freopen("stitch.out","w",stdout);
#endif
scanf("%d%d",&n,&m);
Init(1);Init(-1);
for(int i=1;i<=n+1;i++)
for(int j=1;j<=m+1;j++){
int now=Get(i,j);
if(!f[now]||vis[now])continue;
res=0;
dfs(now);
ans+=res?(res>>1):1;
}
printf("%d
",ans);
return 0;
}