【考试反思】联赛模拟测试18

暴力选手，论如何在 ( exttt{HZOI}) 水到第 8

前面就我没 A 题 = =

T1:施工

思考半小时后无果 (O(nh^2)) 走人。

可以知道，只有两边高，中间低的情况，提升中间的高度才有意义。什么你说两边，我们只需要 (h[0]=INF) 和 (h[n+1]=INF-1) 即可。

设 (f[i]) 表示 (f[i]) 高度不变，从前找到上一个没有改变高度的建筑为 (j) 的答案。那么 (j+1) 到 (i-1) 一定都比 (i,j) 低且最后他们要推平。

设中间的高度为 (t)，转移式子显然：

[egin{aligned} f_i&=igg(sumlimits_{k=j+1}^{i-1} (t-h_k)^2igg)+c(h[j]+h[i]-2t)\ &=(i-j-1) imes t^2-2igg(c+sumlimits_{k=j+1}^{i-1}h_kigg)t+sumlimits_{k=j+1}^{i-1} h_k^2+c(h[j]+h[i]) end{aligned} ]

（边界要判很多 相信大家都会）

我们可以直接找出二次函数的对称轴利用前缀和计算答案。但这样转移是 (O(n^2)) 的。

考虑如何用单调栈优化转移。我们可以维护一个单调递减栈。当当前的元素比栈顶高的时候，(sta[top-1])，(sta[top]) 和当前元素就能正好构成一个满足条件的形状。这样我们即可 (O(n)) 转移。

Code

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+10;
int n,c;
int h[maxn],f[maxn],sum[2][maxn];

inline int read(){
    int x=0;bool fopt=1;char ch=getchar();
    for(;!isdigit(ch);ch=getchar())if(ch=='-')fopt=0;
    for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-48;
    return fopt?x:-x;
}

inline int Cal(int j,int k,int i){
    int A=i-j-1;//(i-1)-(j+1)+1
    int B=-2*(sum[0][i-1]-sum[0][j])-(i!=n+1)*c-(j!=0)*c;
    int C=sum[1][i-1]-sum[1][j]+(i!=n+1)*h[i]*c+(j!=0)*h[j]*c;
    int t=round(-1.0*B/(2*A));//对称轴
    t=max(t,h[k]);t=min(t,min(h[i],h[j]));
    return A*t*t+B*t+C;
}

int sta[maxn],top;
signed main(){
#ifndef LOCAL
    freopen("construct.in","r",stdin);
    freopen("construct.out","w",stdout);
#endif
    n=read();c=read();
    for(int i=1;i<=n;i++){
        h[i]=read();
        sum[0][i]=sum[0][i-1]+h[i];
        sum[1][i]=sum[1][i-1]+1LL*h[i]*h[i];
    }
    h[0]=maxn;h[n+1]=maxn-1;
    sta[++top]=0;
    for(int i=1;i<=n+1;i++){
        f[i]=f[i-1]+((i==1||i==n+1)?0:abs(h[i]-h[i-1])*c);
        while(top&&h[sta[top]]<=h[i]){
            f[i]=min(f[i],f[sta[top-1]]+Cal(sta[top-1],sta[top],i));
            top--;
        }
        sta[++top]=i;
    }
    printf("%lld
",f[n+1]);
    return 0;
}

T2:蔬菜

人均分 58

正解是四维偏序，但是我们怎么可能写正解呢？

题目显然可以离线，发现本题就是小B的询问放在二维上。那么做法就显然了：二维莫队。

二维莫队和一维莫队的区别就是转移不是单点加减，而是一行或者一列。这个我们用 for 循环就可以解决了。

要注意的点就是一定要先 add 后 del，否则本题会开心的 WA 0 pts。QwQ

时间复杂度是 (O(nqsqrt n))。看起来可能不对，但事实上不卡常都跑的飞快～

Code

#include <bits/stdc++.h>
using namespace std;
const int maxn=200+10;
const int maxq=1e5+10;
int n,m,q,nS,mS,tot;
map<int,int> mp;
int g[maxn][maxn];

struct Node{
    int X0,Y0,X1,Y1,id;
    friend inline bool operator <(register const Node& A,register const Node& B){//长度爆炸的排序
        return (A.X0/nS)^(B.X0/nS)?A.X0<B.X0:((A.Y0/mS)^(B.Y0/mS)?A.Y0<B.Y0:((A.X1/nS)^(B.X1/nS)?A.X1<B.X1:A.Y1/mS<B.Y1/mS));
    }
}ask[maxq];

inline int read(){
    int x=0;bool fopt=1;char ch=getchar();
    for(;!isdigit(ch);ch=getchar())if(ch=='-')fopt=0;
    for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-48;
    return fopt?x:-x;
}

int ans,l,r,u,d;;
int res[maxq],cnt[maxn*maxn];
void add(int pos,bool opt){//1:row 0:col
    if(opt){
        for(int i=l;i<=r;i++){
            ans+=2*cnt[g[pos][i]]+1;
            cnt[g[pos][i]]++;
        }
    }else{
        for(int i=u;i<=d;i++){
            ans+=2*cnt[g[i][pos]]+1;
            cnt[g[i][pos]]++;
        }
    }
}

void del(int pos,bool opt){
    if(opt){
        for(int i=l;i<=r;i++){
            ans+=-2*cnt[g[pos][i]]+1;
            cnt[g[pos][i]]--;
        }
    }else{
        for(int i=u;i<=d;i++){
            ans+=-2*cnt[g[i][pos]]+1;
            cnt[g[i][pos]]--;
        }
    }
}

int main(){
#ifndef LOCAL
    freopen("vegetable.in","r",stdin);
    freopen("vegetable.out","w",stdout);
#endif
    n=read();m=read();q=read();
    nS=sqrt(n);mS=sqrt(m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            g[i][j]=read();
            if(!mp[g[i][j]])mp[g[i][j]]=++tot;
            g[i][j]=mp[g[i][j]];
        }
    for(int i=1;i<=q;i++){
        int X0=read(),Y0=read(),X1=read(),Y1=read();
        ask[i]=(Node){X0,Y0,X1,Y1,i};
    }
    sort(ask+1,ask+q+1);
    l=1;r=0;u=1;d=0;
    for(int i=1;i<=q;i++){
        int X0=ask[i].X0,Y0=ask[i].Y0,X1=ask[i].X1,Y1=ask[i].Y1;
        while(u>X0)add(--u,1);
        while(l>Y0)add(--l,0);
        while(d<X1)add(++d,1);
        while(r<Y1)add(++r,0);
        while(u<X0)del(u++,1);
        while(l<Y0)del(l++,0);
        while(d>X1)del(d--,1);
        while(r>Y1)del(r--,0);
        res[ask[i].id]=ans;
    }
    for(int i=1;i<=q;i++)
        printf("%d
",res[i]);
    return 0;
}

T3:联盟

神仙题，160 多行 (O(n^4)) 暴力水了 20

显然需要求树的直径后在直径上枚举边删除两子树合并直径计算贡献。换根 DP 一遍解决，实现能力为 0。

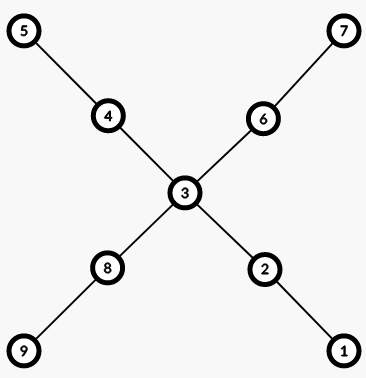
当出现两条直径交叉的时候（如下），无论怎么修改都是无法使答案更优的，这种情况删所有边都可以（但是并没有这个数据导致特判骗分失败）

---

直接为聋跌引流了

T4:水滴

所以为什么要把最简单的题放在最后啊，我还以为是什么毒瘤数据结构所以没想

正解是尺取法转移，时间复杂度 (O(n))。多测不清空，爆零两行泪。

Code

#include <bits/stdc++.h>
using namespace std;
const int maxn=2e5+10;
const int INF=0x3f3f3f3f;
int n,K,R,ans=INF;
int d[maxn],B[maxn],cnt[maxn];
bool lim[maxn];

inline int read(){
    int x=0;bool fopt=1;char ch=getchar();
    for(;!isdigit(ch);ch=getchar())if(ch=='-')fopt=0;
    for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-48;
    return fopt?x:-x;
}

int main(){
#ifndef LOCAL
    freopen("drop.in","r",stdin);
    freopen("drop.out","w",stdout);
#endif
    int T=read();
    while(T--){
        ans=INF;
        memset(lim,0,sizeof(lim));
        memset(cnt,0,sizeof(cnt));
        n=read();K=read();R=read();
        for(int i=1;i<=n;i++)
            d[i]=read();
        for(int i=1;i<=R;i++){
            B[i]=read();cnt[B[i]]=read();lim[B[i]]=1;
        }
        int last=R;
        for(int i=1,j=1;j<=n;j++){
            cnt[d[j]]--;
            if(lim[d[j]]&&!cnt[d[j]])last--;
            while(!last&&i<j){
                ans=min(ans,j-i+1);
                if(lim[d[i]]&&!cnt[d[i]])last++;
                cnt[d[i]]++;
                i++;
            }
        }
        if(ans==INF)puts("DESTROY ALL");
        else printf("%d
",ans);
    }
    return 0;
}

---

做计数去了 = =