概述
一般排序算法的应用背景为顺序表,最大的特点就是可以随机访问,即根据数组下标访问相应的数组元素。而链表是无法随机访问的,每一个结点都需要从头遍历去访问,这就使得利用下标来实现排序的一般算法在面对链表时,需要进行针对性的修改。同时,区别于只存储值的一般数组,结点的存储结构要复杂得多(数据域、指针域等),于是在交换类排序算法中,又会分为交换值(不交换结点地址)和交换结点两种实现方式。
以下针对链表排序的几种常见排序方法进行逐一讲解,代码实现均为C。
链表结构
结构定义
本文的链表均为双向链表,数据结构如下,设虚拟头结点,而非头指针,使用id定位数据元素,而非标号(下标):
typedef struct Node { int val, id; struct Node *next, *pre; } Node; typedef struct DList { Node head; int length; } DList;
结构操作
结点插入采用头插法,即新结点均是从虚拟头结点后插入链表的。
Node *getNewNode(int val, int id) { Node *node = (Node *)malloc(sizeof(Node)); node->val = val; node->id = id; node->next = NULL; node->pre = NULL; return node; } DList *init_dlist() { DList *l = (DList *)malloc(sizeof(DList)); l->head.next = NULL; l->head.pre = NULL; l->length = 0; return l; } void clear_node(Node *node) { if (node == NULL) return; free(node); return; } void clear(DList *l) { if (l == NULL) return; Node *p = l->head.next, *q; while (p) { q = p->next; clear_node(p); p = q; } free(l); return; } //采用头插法 int insert(DList *l, int val, int id) { if (l == NULL) return 0; Node *node = getNewNode(val, id); node->pre = &(l->head); node->next = l->head.next; if (l->head.next) l->head.next->pre = node; l->head.next = node; l->length += 1; return 1; } int erase(DList *l, int id) { if (l == NULL) return 0; if (id < 0 || id >= l->length) return 0; Node *p = &(l->head), *q; while (p->next->id != id) p = p->next; q = p->next; p->next = q->next; if (p->next) p->next->pre = p; clear_node(q); l->length -= 1; return 1; } void l_output(DList *l) { if (l == NULL) return; printf("DList : ["); for (Node *p = l->head.next; p; p = p->next) { printf("%d(%d)->", p->val, p->id); } printf("NULL] "); return; } void r_output(DList *l) { if (l == NULL) return; printf("DList : ["); Node *tail = &(l->head); while (tail->next != NULL) tail = tail->next; for(;tail->pre != NULL; tail = tail->pre) { printf("%d(%d)->", tail->val, tail->id); } printf("head] "); return; }
虚拟头结点
链表排序为了方便,不同算法对虚拟头结点的处理情况不同。
有的是从虚拟头结点开始(即传入DList,返回也是DList);
有的则是从真正的第一个结点开始(即直接传入Node,返回也是Node),此时的head并非指虚拟头结点,而是链表中真正参与排序的第一个节点;
注意分辨!
交换类排序
上文提到,交换类排序的核心函数swap的实现分两种情况:交换值和交换结点。
交换值
比较简单,直接设一个tmp值交换即可(也可考虑异或^运算交换值):
void swap1(Node *node1, Node *node2){ int val = node1->val; node1->val = node2->val; node2->val = val; return; }
交换结点
交换结点则比较复杂,主要是前后连接关系(指针域)的更新。考虑到相邻结点的特殊情况,又可以分为两种来进行讨论:
相邻
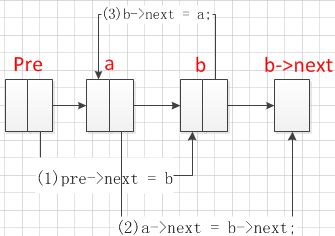
void swap2_1(Node *node1, Node &node2) { // next node1->pre->next = node2; node1->next = node2->next; node2->next = node1; // pre node1->next->pre = node1; node2->pre = node1->pre; node1->pre = node2; return; }
不相邻
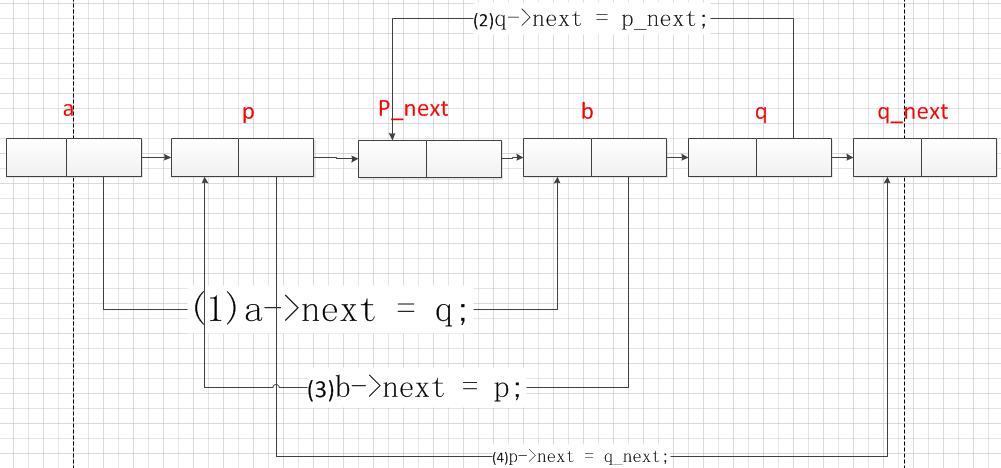
void swap2_2(Node *node1, Node &node2) { Node *tmp1 = node1->next; Node *tmp2 = node2->pre; // next if (node1->pre) node1->pre->next = node2; tmp2->next = node1; node1->next = node2->next; node2->next = tmp1; // pre tmp1->pre = node2; if (node1->next) node1->next->pre = node1; node2->pre = node1->pre; node1->pre = tmp2; return; }
冒泡排序
时间复杂度$O(n^2)$,空间复杂度$O(1)$。
交换结点值val
void BubbleSortList(Node *head) { if (head == NULL || head->next == NULL) return head; Node *p = NULL; int ischange = 1; while (p != head->next && ischange) { Node *q = head; ischange = 0; for (; q && q->next != p; q = q->next) { if (q->val > q->next->val) { swap1(q, q->next); ischange = 1; } } p = q; } return head; }
交换结点
属于相邻交换,注意 p->next 的变化。
Node *BubbleSortList(Node *head) { if (head == NULL || head->next == NULL) return head; Node *p = NULL; int ischange = 1; while (p != head->next && ischange) { Node *q = head; ischange = 0; for (; q && q->next != p;) { if (q->val > q->next->val) { swap2_1(q, q->next); ischange = 1; } q = q->next; } p = q; } return head; }
快速排序
一般快速排序在partition时的前后区间都采用闭区间,即边界参数分别取 mid - 1 和 mid + 1 。而链表排序中,如果也按这种两边都是闭区间的话,找到mid后还得再遍历一次找到 mid - 1 。所以,为了方便操作,链表的快速排序采用前闭后开的形式,即边界参数分别取 mid 和 mid->next (注意主函数调用时的参数为 head 和 NULL )。
平均时间复杂度$O(nlog n)$,不考虑递归栈空间的话空间复杂度是$O(1)$。
交换值
DList *QuickSortList(DList *l) { if (l->head.next == NULL || l->head.next->next == NULL) return l; qSortList(l->head.next, NULL); return l; } void *qSortList(Node *head, Node *tail) { if (head != tail || head->next != tail) { Node *mid = partiotionList1(head, tail); //Node *mid = partiotionList2(head, tail); qSortList(head, mid); qSortList(mid, tail); } return; } Node *partiotionList1(Node *low, Node *high) { int key = low->val; Node *p = low; for (Node *q = low->next; q != high; q = q->next) { if (q->val < key) { p = p->next; swap1(p, q); } } swap1(p, low); return p; }
交换节点
只有partiotion的swap部分不一样:
Node *partiotionList2(Node *low, Node *high) { int key = low->val; Node *p = low; for (Node *q = low->next; q != high;) { if (q->val < key) { p = p->next; if (p == q) q = q->next; else { if (p->next == q) swap2_1(p, q); else swap2_2(p, q); Node *tmp = p; p = q; q = tmp->next; } } } if (low == p) return low; if (low->next == p) swap2_1(low, p); else swap2_2(low, p); return low; }
插入排序
比较简单,直接更新连接关系(指针域)即可。时间复杂度为$O(n^2)$,空间复杂度为$O(1)$。
DList *InsertSortList(DList *l) { if (l->head.next == NULL || l->head.next->next == NULL) return l; Node *current_node = l->head.next->next; //指向待插入结点 while (current_node) { Node *p = l->head.next; while (p != current_node && current_node->val >= p->val) { p = p->next; } if (p == current_node) current_node = current_node->next; else { Node *tmp = current_node->pre; tmp->next = current_node->next; if (current_node->next) current_node->next->pre = tmp; p->pre->next = current_node; current_node->pre = p->pre; p->pre = current_node; current_node->next = p; current_node = tmp->next; } } return l; }
选择排序
也是更新连接关系(指针域)。时间复杂度为$O(N^2)$,空间复杂度为$O(1)$。
DList *SelectsortList(DList *l) { if (l->head.next == NULL || l->head.next->next == NULL) return l; Node *current_node = l->head.next; //指向待插入的最小节点位置 while (current_node) { Node *min = current_node, *p = min->next; while (p) { if (p->val < min->val) { min = p; } p = p->next; } if (min == current_node) current_node = current_node->next; else { Node *tmp = min->pre; tmp->next = min->next; if (min->next) min->next->pre = tmp; current_node->pre->next = min; min->next = current_node; min->pre = current_node->pre; current_node->pre = min; current_node = tmp->next; } } return l; }
归并排序
可以说是链表排序的最佳方法了。
由于不涉及交换,算法思想与链表结构的契合度也好,且保证了最好和最坏时间复杂度都是$O(nlog n)$,同时它在数组排序中广受诟病的空间复杂度在链表排序中也从$O(n)$降到了$O(1)$,所以说归并排序是链表排序的最优选择。
首先用快慢指针的方法找到链表中间节点,然后递归地对两个子链表排序,把两个排好序的子链表合并成一条有序的链表。
注意这里的head均非虚拟头结点,而是真正的第一个排序节点。
Node *mSortList(Node *head1, Node *head2) { if (head1 == NULL) return head2; if (head2 == NULL) return head1; Node *res, *p; if (head1->data < head2->data) { res = head1; head1 = head1->next; } else { res = head2; head2 = head2->next; } p = res; while (head1 != NULL && head2 != NULL) { if (head1->data < head2->data) { p->next = head1; head1->pre = p; head1 = head1->next; } else { p->next = head2; head2->pre = p; head2 = head2->next; } p = p->next; } if (head1 != NULL) { p->next = head1; head1->pre = p; } else if (head2 != NULL) { p->next = head2; head2->pre = p; } return res; } Node *MergeSortList(Node *head) { if (head == NULL || head->next == NULL) return head; //使用快慢指针定位中点进行partition Node *fast = head, *slow = head; while (fast->next != NULL && fast->next->next != NULL) { fast = fast->next->next; slow = slow->next; } fast = slow; slow = slow->next; fast->next = NULL; slow->pre = NULL; fast = my_msort(head); slow = my_msort(slow); return merge(fast, slow); }
不适合链表的排序算法
对于希尔排序,因为排序过程中经常涉及到arr[i+gap]操作,其中gap为希尔排序的当前步长,这种操作不适合链表。
对于堆排序,一般是用数组来实现二叉堆,当然可以用二叉树来实现,但是这么做太麻烦,还得花费额外的空间构建二叉树。
链表排序的典型应用
邻值查找
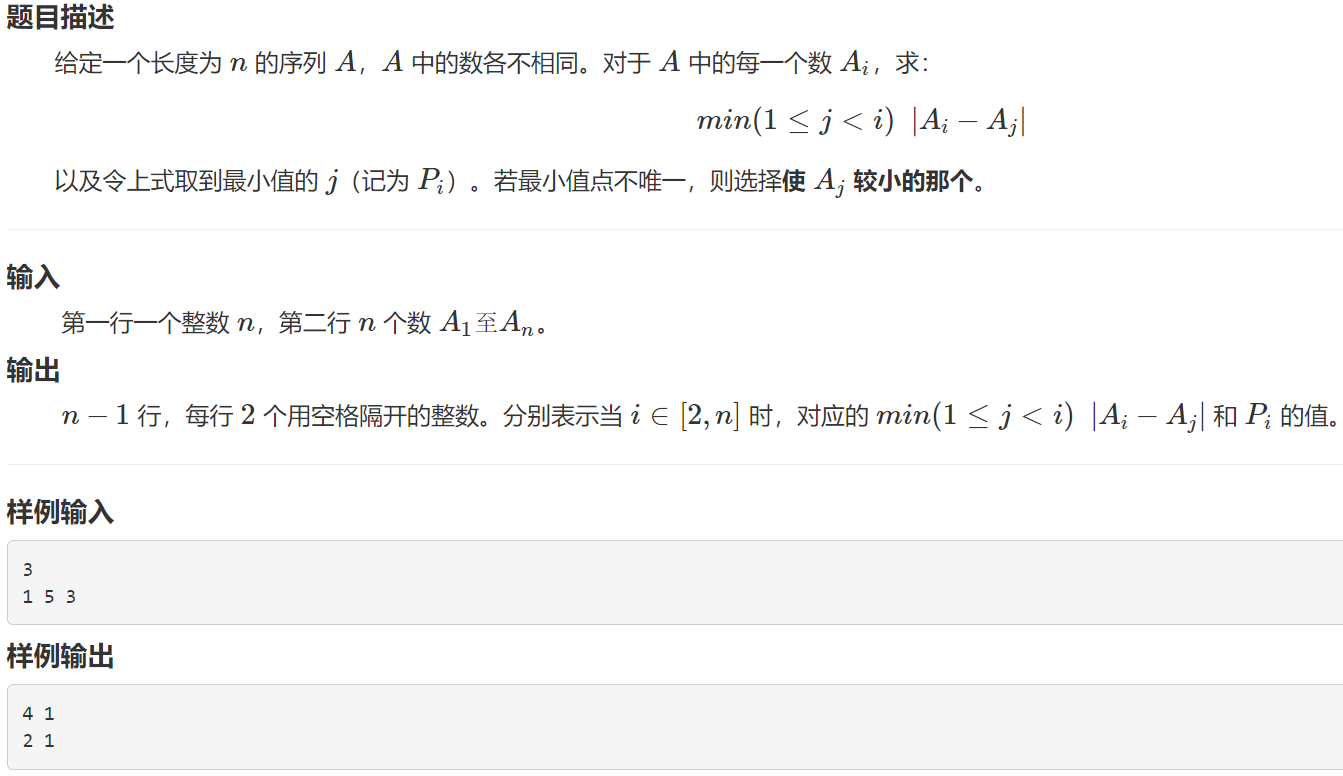
解题思路
采用双向链表的数据结构。先将链表有序化,则每一个结点的最小距离必在离它最近的两个结点上产生(即 node->pre 和 node->next )。同时,考虑到先出现的结点的最小距离可能受到后出现的邻居结点的干扰(即当前节点的最小距离结点如果是在它之后出现的结点,则实际为无效结点),可以倒过来从最后结点往前求最小距离,每次求得当前结点的最小距离后将该结点从链表中删除,则可避免出现无效的情况。
代码实现(C)

#include <stdio.h> #include <stdlib.h> int *min, *rid; typedef struct Node { int val, id; struct Node *next, *pre; } Node; typedef struct DList { Node head; int length; } DList; Node *getNewNode(int val, int id) { Node *node = (Node *)malloc(sizeof(Node)); node->val = val; node->id = id; node->next = NULL; node->pre = NULL; return node; } DList *init_dlist() { DList *l = (DList *)malloc(sizeof(DList)); l->head.next = NULL; l->head.pre = NULL; l->length = 0; return l; } void clear_node(Node *node) { if (node == NULL) return; free(node); return; } void clear(DList *l) { if (l == NULL) return; Node *p = l->head.next, *q; while (p) { q = p->next; clear_node(p); p = q; } free(l); return; } //采用头插法 int insert(DList *l, int val, int id) { if (l == NULL) return 0; Node *node = getNewNode(val, id); node->pre = &(l->head); node->next = l->head.next; if (l->head.next) l->head.next->pre = node; l->head.next = node; l->length += 1; return 1; } int erase(DList *l, int id) { if (l == NULL) return 0; if (id < 1 || id > l->length) return 0; Node *p = &(l->head), *q; while (p->next->id != id) p = p->next; q = p->next; p->next = q->next; if (p->next) p->next->pre = p; clear_node(q); l->length -= 1; return 1; } void l_output(DList *l) { if (l == NULL) return; printf("DList : ["); for (Node *p = l->head.next; p; p = p->next) { printf("%d(%d)->", p->val, p->id); } printf("NULL] "); return; } void r_output(DList *l) { if (l == NULL) return; printf("DList : ["); Node *tail = &(l->head); while (tail->next != NULL) tail = tail->next; for(;tail->pre != NULL; tail = tail->pre) { printf("%d(%d)->", tail->val, tail->id); } printf("head] "); return; } //注意这里的head并非虚拟头结点,而是真正的第一个排序节点 Node *merge(Node *head1, Node *head2) { if (head1 == NULL) return head2; if (head2 == NULL) return head1; Node *res, *p; if (head1->val < head2->val) { res = head1; head1 = head1->next; } else { res = head2; head2 = head2->next; } p = res; while (head1 != NULL && head2 != NULL) { if (head1->val < head2->val) { p->next = head1; head1->pre = p; head1 = head1->next; } else { p->next = head2; head2->pre = p; head2 = head2->next; } p = p->next; } if (head1 != NULL) { p->next = head1; head1->pre = p; } else if (head2 != NULL) { p->next = head2; head2->pre = p; } return res; } Node *my_msort(Node *head) { if (head == NULL || head->next == NULL) return head; //使用快慢指针定位中点进行partition Node *fast = head, *slow = head; while (fast->next != NULL && fast->next->next != NULL) { fast = fast->next->next; slow = slow->next; } fast = slow; slow = slow->next; fast->next = NULL; slow->pre = NULL; fast = my_msort(head); slow = my_msort(slow); return merge(fast, slow); } void my_find(DList *l, int id) { Node *p = l->head.next; while(p->id != id) p = p->next; if (p->pre != &(l->head)) { *(min + id) = abs(p->pre->val - p->val); *(rid + id) = p->pre->id; } if (p->next) { int tmp = abs(p->next->val - p->val); if (*(min + id)) { *(rid + id) = *(min + id) <= tmp ? *(rid + id) : p->next->id; *(min + id) = *(min + id) <= tmp ? *(min + id) : tmp; } else { *(min + id) = tmp; *(rid + id) = p->next->id; } } return; } int main() { int n; scanf("%d", &n); DList *l = init_dlist(); rid = (int *)calloc(n + 1, sizeof(int)); min = (int *)calloc(n + 1, sizeof(int)); int val; for (int i = 1; i <= n; i++) { scanf("%d", &val); insert(l, val, i); } l->head.next = my_msort(l->head.next); l->head.next->pre = &(l->head); for (int i = n; i> 1; i--) { my_find(l, i); erase(l, i); } for (int i = 2; i <= n; i++) { i == 2 || putchar(' '); printf("%d %d", *(min + i), *(rid + i)); } return 0; }
规模50000以上会超时,所以需要优化。
优化思路
数据结构由双向链表改进成静态链表,从而实现了随机访问,解决了链表的访问短板,使得时间代价明显减少,顺利AC。

#include <stdio.h> #include <stdlib.h> #define INT_MAX 0x7fffffff int *val, *ind, *pre, *next; int len; int *min, *rid; void output() { printf("Val : ["); for (int i = 1; i <= len; i++) { printf("%d(%d)->", val[i], i); } printf("End] After sort : ["); for (int i = 1; i <= len; i++) { printf("%d(%d)->", val[ind[i]], ind[i]); } printf("End] Rel : ["); for (int i = 1; i <= len; i++) { printf("(%d)%d(%d)->", pre[ind[i]], ind[i], next[ind[i]]); } printf("End] "); return; } int my_merge(int *ind, int *aux, int left, int mid, int right, int tpre) { int i = left, j = mid + 1, k = left; while (i <= mid && j <= right) { if (val[aux[i]] <= val[aux[j]]) { ind[k] = aux[i++]; } else { ind[k] = aux[j++]; } pre[ind[k]] = tpre; next[tpre] = ind[k]; tpre = ind[k++]; } while (i <= mid) { ind[k] = aux[i++]; pre[ind[k]] = tpre; next[tpre] = ind[k]; tpre = ind[k++]; } while (j <= right) { ind[k] = aux[j++]; pre[ind[k]] = tpre; next[tpre] = ind[k]; tpre = ind[k++]; } return ind[left]; } void my_msort(int *ind, int *aux, int left, int right) { if (left >= right) return; int mid = (left + right) >> 1; my_msort(aux, ind, left, mid); my_msort(aux, ind, mid + 1, right); next[aux[left - 1]] = my_merge(ind, aux, left, mid, right, aux[left - 1]); return; } void my_sort() { int *aux = (int *)malloc(sizeof(int) * (len + 1)); for (int i = 0; i <= len; i++) aux[i] = ind[i]; my_msort(ind, aux, 1, len); free(aux); return; } /*int find_id(int *ind, int i) { int low = 1, high = len, mid; while (low <= high) { mid = (low + high) >> 1; if (ind[mid] == i) return mid; else if (val[ind[mid]] > val[i]) high = mid - 1; else low = mid + 1; } return -1; }*/ void my_nn(int id) { printf("target = %d ", val[id]); int min1 = INT_MAX, min2 = INT_MAX; printf("min1 = %d, min2 = %d ", min1, min2); if (pre[id]) { min1 = abs(val[pre[id]] - val[id]); printf("pre[id] = %d, min1 = %d ", pre[id], min1); } if (next[id]) { min2 =abs(val[next[id]] - val[id]); printf("next[id] = %d, min2 = %d ", next[id], min2); } min[id] = min1 <= min2 ? min1 : min2; rid[id] = min1 <= min2 ? pre[id] : next[id]; return; } int main() { scanf("%d", &len); val = (int *)malloc(sizeof(int) * (len + 1)); pre = (int *)calloc(len + 1, sizeof(int)); next = (int *)calloc(len + 1, sizeof(int)); ind = (int *)calloc(len +1, sizeof(int)); min = (int *)calloc(len + 1, sizeof(int)); rid = (int *)calloc(len +1, sizeof(int)); int tmp; for (int i = 1; i <= len; i++) { scanf("%d", &tmp); val[i] = tmp; ind[i] = i; } my_sort(); output(); for (int i = len; i > 1; --i) { my_nn(i); next[pre[i]] = next[i]; pre[next[i]] = pre[i]; } for (int i = 2; i <= len; i++) { printf("%d %d ", min[i], rid[i]); } free(val); free(pre); free(next); free(ind); free(min); free(rid); return 0; }
(代码均为原创)
参考资料:
https://blog.csdn.net/qq_35644234/article/details/53222603
https://www.cnblogs.com/TenosDoIt/p/3666585.html
https://www.cnblogs.com/demian/p/7895676.html
