决策单调性:
对于一些dp方程,经过一系列的猜想和证明,可以得出,所有取的最优解的转移点(即决策点)位置是单调递增的。
即:假设f[i]=min(f[j]+b[j]) (j<i) 并且,对于任意f[i]的决策点g[i],总有f[i+1]的决策点g[i+1]>=g[i](或者<=g[i]) 那么,这个方程就具备决策单调性。
这个有什么用吗?
不懂具体优化方法的话确实也没有什么用。可能还是n^2的。只不过范围可能少了一些。
一
经典入门例题:
Description:
[POI2011]Lightning Conductor
已知一个长度为n的序列a1,a2,...,an。
对于每个1<=i<=n,找到最小的非负整数p满足 对于任意的j, aj < = ai + p - sqrt(abs(i-j))
Solution:
题目转化一下:就是对于每个i,找到aj+sqrt(abs(i-j))的最大值。
首先必须要先证明决策单调性:
当i>j时,即aj+sqrt(i-j)<=ai
假设对于i位置的决策点为g[i],那么对于任意的正数k,满足a[g[i]-k] + sqrt(i-g[i]+k) <= a[g[i]] + sqrt(i-g[i])
当i变成i+1 的时候, 因为幂函y = sqrt(x)是下凸的,
因为i-g[i]+k < i-g[i]
所以,sqrt(i+1-g[i]+k)-sqrt(i-g[i]+k) < sqrt(i+1-g[i]) - sqrt(i-g[i]) (越大,加1越不明显)
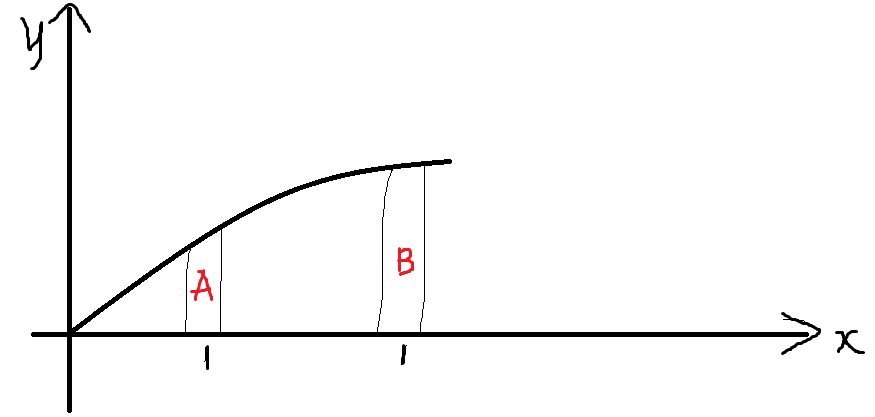
大概就是,A区域一段的增加幅度大于B区域一段。
所以:a[g[i]-k] + sqrt(i+1-g[i]+k) < a[g[i]] + sqrt(i+1-g[i]) 不选的那个点更不优了。g[i+1]>=g[i] 所以有单调性。
当j>i 的时候,同理可证。
处理方法:
1.分治:
sol(l,r,L,R) 表示决策l,r这段区间,决策点可能在L,R。
每次取一个mid=(l+r)/2 , 暴力扫描L,R找到决策点id。分治到:sol(l,mid-1,L,id) 和 sol(mid+1,r, id,R)
因为对于>mid 的点,决策一定比id大。反过来同理。
logn层,每层扫描总共O(n) 复杂度nlogn
这个题用这个方法代码好写。
注意理解一下i<j和i>j的情况两次找。
#include<bits/stdc++.h> using namespace std; const int N=500000+10; double f[N][2]; int a[N],n; void sol(int l,int r,int L,int R,int ty){ if(l>r) return; int mid=(l+r)>>1;int id=0; for(int i=L;i<=min(R,mid);i++){//注意,这里min(R,mid),每次只从前部分取max //保证了i<j或者i>j的前提下的决策单调性。(虽然看似都是j<i的单调性,但是我对称数组了呀) //可以根据题目样例画图理解一下 if(1.0*a[i]+1.0*sqrt(1.0*abs(i-mid))>f[mid][ty]){ f[mid][ty]=1.0*a[i]+1.0*sqrt(1.0*abs(i-mid)); id=i; } } sol(l,mid-1,L,id,ty);sol(mid+1,r,id,R,ty); } int main() { cin>>n; for(int i=1;i<=n;i++) scanf("%d",&a[i]); sol(1,n,1,n,1); for(int i=1;i<=n/2;i++) swap(a[i],a[n-i+1]);//这里要对称一下,正反分别找一遍, //对应i<j和i>j的情况,这样决策才是一直单调的。 sol(1,n,1,n,0); for(int i=1;i<=n;i++){ int ans=(int)ceil(f[i][1])-a[n-i+1]; int aa=(int)ceil(f[n-i+1][0])-a[n-i+1]; ans=max(ans,aa); printf("%d ",ans); } return 0; }
缺陷在于:这个方法必须依赖于f[i]与之前的f们无关。因为先得出答案的是区间中间的值,没有任何顺序。
一般适用于二维dp —— SD_le
(因为,二维dp一般有f[i][k]=min(f[j][k-1]),f[j][k-1]们已经在之前算好了。就可以直接分治。不用考虑得出答案的顺序)
2.队列:
这个方法适用性比较普遍。
我们把思路转化一下,从考虑每个位置的决策点,到每个点是哪些位置的决策点。
根据决策单调性,这些位置一定是连续的一段区间。
从前到后1~n枚举i
每次枚举到i,就从队头取出最优解,更新答案。再用二分查找决策分界点。插入队尾。
具体解释:
维护一个队列,队列里存着三元组(id,l,r),表示决策点和以id为最优决策点的区间(l,r)i从1扫到n
①i的最优决策点一定是队头的id,然后如果队头的r==i,弹出队头
②以i为最优决策点的区间一定是(x,n],然后从队列尾开始,如果队尾的q[tail].id在q[tail].l~q[tail].r中全劣于i,弹出队尾。
③当前队尾的元素在l~r中可能前一部分优于i,后一部分劣于i,二分这个分界点,修改q[tail].r
④如果q[tail].r!=n,将(i,q[tail].r+1,n)加入队尾
概括地说,1.取队头,2.判断弹队头 3.新决策点二分一个影响区间 4. 弹出队尾,或者弹出自己或者改变队尾区间影响范围。(5.加入自己)
不断循环3、4步,直到弹出自己或者改变范围。
循环当前的i,二分,nlogn
对于这个题,就是每次的i,找队头的id,更新f[i],把自己加进去。
因为每次决策点都是之前的,所以也要对称数组再做一遍即可。
二
土地购买、玩具装箱也可以用决策单调性。
但是斜率优化毕竟O(n)更好。
三
[Lydsy1712月赛]小Q的书架
题面:https://www.lydsy.com/JudgeOnline/upload/201712/prob12.pdf
f[i][k]表示,前i个位置,在i后面砍第k刀的最小代价。
f[i][k]=min(f[j][k-1]+w(j+1,i)) j<i
w(l,r)即为l到r区间内的逆序对数量。
w显然满足四边形不等式。
用什么方法处理单调性呢?
发现,既然k从k-1转移,我们不妨从小到大枚举k
f[i][k-1]们都求出来了,所以可以直接分治。(毕竟分治好写)
至于w(l,r)
每次统计,就变成优秀的n^2logn“分治”了。
所以,用莫队思想。每次动一点。
复杂度肯定要优秀一些。但是不会证。。。
大概复杂度:
O(nksqrt(n)*logn+nlogn)实际莫队表现好像更快。
代码:
值得注意的是,R-L+1-query(a[R+1]-1)求区间多少个比a[R+1]大的。总的减去小的。
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=40000+5; int n,m; int f[N][12]; int t[N]; int a[N]; void add(int x,int c){ for(;x<=n;x+=x&(-x)) t[x]+=c; } int query(int x){int ret=0; for(;x;x-=x&(-x)) ret+=t[x]; return ret; } int ni; int L,R; void mov(int l,int r){ //cout<<l<<" and "<<r<<endl; //cout<<L<<" ;; "<<R<<endl; while(R<r) ni+=(R-L+1-query(a[R+1]-1)),add(a[++R],1); while(L>l) ni+=query(a[L-1]-1),add(a[--L],1); while(R>r) ni-=(R-L-query(a[R]-1)),add(a[R--],-1); while(L<l) ni-=query(a[L]-1),add(a[L++],-1); } void divi(int p,int l,int r,int L,int R){ //cout<<p<<" "<<l<<" "<<r<<" : "<<L<<" "<<R<<endl; if(L>R) return; int mid=(L+R)/2; int id=0; for(int i=min(mid-1,r);i>=l;i--){ mov(i+1,mid); //cout<<" jj"<<endl; if(f[i][p-1]+ni<f[mid][p]){ f[mid][p]=f[i][p-1]+ni; id=i; } } divi(p,l,id,L,mid-1); divi(p,id,r,mid+1,R); } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++)scanf("%d",&a[i]); memset(f,0x3f,sizeof f); f[0][0]=0; L=1,R=1; add(a[1],1); for(int k=1;k<=m;k++){ //cout<<" now "<<k<<endl; divi(k,0,n-1,1,n); } printf("%d",f[n][m]); return 0; }
决策单调性感觉非常微妙,是的,微妙。
必须要往这方面去想。1e5数据范围
一般要通过推式子。(打表找规律)
证明单调性后,就比较套路了。