[SDOI2009]Bill的挑战——全网唯一 一篇容斥题解

全网唯一一篇容斥题解

Description

Solution

看到这个题，大部分人想的是状压dp

但是我是个蒟蒻没想到，就用容斥切掉了。

并且复杂度比一般状压低，

（其实这个容斥的算法，提出来源于ywy_c_asm）

（然而我知道了这个算法，竟然和他写的不一样，而且比他跑的快）

进入正题：

我们需要统计恰好满足匹配k个的情况。

那么，我们可以先找出来，恰好满足n个，n-1，n-2。。。k个的情况。

分别记为ans[i]

ans[i]怎么算呢？

先给出公式：

ans[i]=cal(i)-∑C(j,i)×ans[j] 其中，i+1<=j<=n

cal(i)表示，从n个中任意选择i个，对于所有选择的情况，的方案数的和。

cal(i)可以dfs暴力C(n,i)枚举，每次统计答案。计入tot

void dfs(int x,int has){
    if(x==n+1){
        if(has!=up) return;
        ll lp=1;
        for(int j=1;j<=len;j++){
            las=-1;
            for(int i=1;i<=up;i++){
                if(a[mem[i]][j]!='?'){
                    if(las==-1){
                        las=a[mem[i]][j]-'a';
                    }
                    else if(las!=a[mem[i]][j]-'a') return;
                }
            }
            if(las==-1)lp=(lp*26)%mod;
        }
        (tot+=lp)%=mod;
        return;
    }
    if(has<up) {
        mem[++cnt]=x;
        dfs(x+1,has+1);
        mem[cnt--]=0;
    }
    if(n-x>=up-has) dfs(x+1,has);
}

至于后面减去的部分。就是容斥的内容了。

大家可以自己画一个韦恩图理解一下。

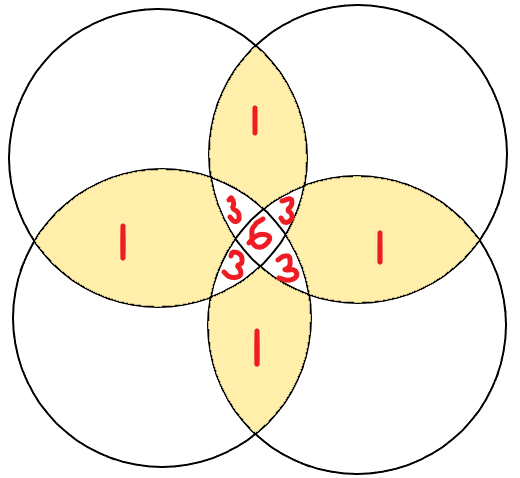
这里有一个例子：n=4

现在我们要算ans[2],也就是恰好匹配2个的T的方案数

就是黄色的部分。

红色的数字是这个区域被算cal(i)的次数。

可见，三个点的重复区域，由于有C(3,2)种方法选到，所以会被算C(3,2)次。

所以减去所有的ans[3]即可。

其他情况同理。

最后输出ans[1]

组合数打表。

理论复杂度：
O(n×len×2^15)

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=20;
const int M=52;
const int mod=1000003;
char a[N][M];
int len;
int n,t,k;
int mem[N],cnt;
ll ans[N];
ll c[N][N];
ll sum;
ll tot;//tot measures
int up;//choose 
int las;
void dfs(int x,int has){//dfs计算tot 
    if(x==n+1){
        if(has!=up) return;
        ll lp=1;
        for(int j=1;j<=len;j++){
            las=-1;
            for(int i=1;i<=up;i++){
                if(a[mem[i]][j]!='?'){
                    if(las==-1){
                        las=a[mem[i]][j]-'a';
                    }
                    else if(las!=a[mem[i]][j]-'a') return;//两个字符不一样，无合法方案 
                }
            }
            if(las==-1)lp=(lp*26)%mod;//如果都是‘？’可以随便填，否则只有一种 
        }
        (tot+=lp)%=mod;
        return;
    }
    if(has<up) {
        mem[++cnt]=x;
        dfs(x+1,has+1);
        mem[cnt--]=0;
    }
    if(n-x>=up-has) dfs(x+1,has);
}

void clear(){
    memset(ans,0,sizeof ans);
    sum=0;
    len=0;
}
int main()
{
    for(int i=0;i<=N-1;i++){
        c[i][0]=1;
        for(int j=1;j<=i;j++){
            c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
        }
    }
    scanf("%d",&t);
    while(t--){
        clear();//清空数组，其实没有必要 
        scanf("%d%d",&n,&k);
        for(int i=1;i<=n;i++){
            scanf("%s",a[i]+1);
        }
        len=strlen(a[1]+1);//长度 

        for(int i=n;i>=k;i--){//ans[i]计算 
            tot=0;up=i;
            dfs(1,0);
            sum=0;
            for(int j=i+1;j<=n;j++){//容斥的处理 
                (sum+=c[j][i]*ans[j])%=mod;
            }
            ans[i]=(tot-sum+mod)%mod;
        }
        printf("%lld
",ans[k]);
    }
    return 0;
}